Auctions
Contents
Introduction
When you think about an auction, you probably imagine some movie scene from auction house where paintings from famous artists are being auctioned. You might even think about shills, bidders secretly working for the auctioneer, trying to raise the price but that's not all there is to auctions. The most common auction design is called English auction and it is just one of many types of auctions used in variety of fields every day. The simplified interaction rules and assumption of rational risk neutral bidders leads to a model which can be studied by the means of game theory.
Definition
An auction is a multi-player game in which a seller (who is not a player), is trying to sell one or more scarce items in a way which maximizes his revenue. The auction can be carried out by a third party, an auctioneer. Players, the buyers, are trying to pay the lowest price possible for the item in order to make profit. The payoff of the winning bidder (the player with the highest bid) is the difference between his valuation of the object and the price paid, zero for others.
Types of auctions
You can categorize auctions according to many criteria most of which are only superficial and unimportant for an analysis from the game theory stand point. The four most important types of auctions are open cry ascending price, open cry descending price auction and first-price and second-price sealed-bid auctions.
Open cry ascending price auction
Open cry ascending price auction, also known as English auction, is the most common auction. After setting the initial price by the auctioneer the bidders place their bids in random order, each bidder can bid as many times as she wants and the auction lasts until there is no player willing to overbid the currently highest bid. The winner pays her bid. In real auctions there is often some minimal amount by which players can raise the bid. Let's assume for the rest of this chapter that such difference is negligible in comparison to the absolute value of the winning bit.
As mentioned above, English auctions are very common when selling art, antiques or memorabilia. Also many online auctions qualify as an English auction because each bidder can see what is the highest current bid and react on such information. Online auctions often have buyout option (not very common in offline auctions) which means, that there is a price ceiling set and auctioneer's revenue may not be maximized. Due to their nature online auctions are time limited which often manifests in high activity and new bids just before the end of the auction, so called sniping.
Open cry descending price auction
Dutch auction or open cry descending price auction is very similar to English auction but as the name suggests the auctioneer sets the initial price high and gradually lowers it. The winner is the bidder who bids first, the bids of other players are not revealed. The auctioneer usually sets a minimum price she is willing to accept, if this minimal price is reached without any bids, the item is not sold. The name comes from the most notable use of this auction type - selling flower auctions in Netherlands.
Dutch auction is also very useful for selling multiple identical items. For example U.S. Department of the Treasury uses single-price auction, modification of Dutch auction, for selling T-bills (U.S. Department of the Treasury, Bureau of the Public Debt, 2012). The bidders bid for multiple T-bills with item price and the auction stops only when enough bids are placed so that they cover the whole amount that is being sold. All the winners then pay the lowest winning price, hence single-price auction, and their demands are satisfied from the highest bid to the lowest one (the last winner may not get the whole amount she bid for).
First-price sealed-bid auction
In a sealed-bid auction each player submits a single bid in secrecy so that only she knows it; the auctioneer reviews all bids and finds the winning one. The winner pays her (the highest) bid as the price. A first-price sealed-bid auction is often employed as a reverse auction, i.e. the auctioneer is not trying to sell some good but buy it, the winning bid is the lowest one. Typical use is in government tenders. Luckily the analysis is the same for auction and reverse auction only the terms are flipped, for consistency only the selling auction will be considered from now on.
Second-price sealed-bid auction
Second-price sealed-bid auction is known as Vickrey auction after its inventor, an American mathematician William Vickrey. Second price means that the winner pays the second highest bid. This may seem counterintuitive but as we will see later on this leads to Vickrey auction being value revealing. Vickrey auction is rarely used in practice. There are two reasons for that: it is not efficient in situations when bidders are unsure of their evaluations (common value auctions) and more importantly it doesn't maximize auction proceeds. A real-life example of generalized Vickrey auction is the Google AdWords system for deciding which ads to display (Google, 2013).
Special types of auctions
There are many types of auctions imaginable, apart from those listed above, some others should be at least mentioned. Walrasian auction is a continuous process in which auctioneer accepts bids from buyers and sellers and computes the clearing price for all transactions (it is basis for some stock exchange mechanisms). In all-pay auction all bidders pay their bids but only the winner gets the item, this model is used for bribery. Bidders bid for packages of items in combinatorial auction, the price paid by bidders is determined so that the total profit of the seller is maximised. Bidding fee auction is a general variation in which a fee is imposed on each bid or the right to enter the auction.
Important aspects of auctions
Private and common value
The cornerstone on which bidding strategy of each player stands is his valuation of the auctioned item. The commonality of the valuation has an impact on the analysis of auctions. Private and common values are extremes on the opposite sides of a spectrum; real-life situations fall somewhere between them. Nevertheless, they are important concepts you should bear in mind when reasoning about an auction.
When we think back to the prototypical auction - art auction - we are very close to a private value situation. Each bidder bases her valuation only on private appreciation of the art piece regardless other bidders' valuations (even if such information is available).
On the other end of the spectrum is the common value. It is a situation in which the objective value of the good is known to all bidders. Simplest example is a dollar auction (auction in which one dollar is auctioned) - the dollar has the same value for all bidders. A real-life situation very close to purely common value auction is auction of mining/drilling permits in certain area auctioned by a government. Each bidder is allowed some test drills and surveys to ascertain the size of the resource and then bids on it. Due to the inaccuracy (imperfect information) of the estimate the real value is unknown prior to the auction even though it is a common value.
Similarity of the auction types
The section on auction types discussed the four most important types of auctions. Analysing all of them would be rather lengthy and possibly tedious. Luckily the four types can be collapsed into two types with some assumptions.
In English (open cry) auction with many bidders the important part is when only two highest bidders are left. If each bidder has in mind her maximal bid based on her private valuation and the increments in bids are small, the two highest bids will be bi and bi - ɛ (e.g. 1,000,001 and 1,000,000). The winner might be willing to go higher (e.g. 1,200,000) but because of the small increments ends up paying just slightly more than the second highest bid. That is essentially the same as a second-price sealed-bid auction. English auction can therefore be modelled as a second-price sealed-bid auction.
It is obvious that in reality there is some minimal increment set by the auctioneer or at least given by a social norm (bidding round numbers in ever increasing steps) which means greater revenue for the auctioneer than in Vickrey auction.
When participating in an open cry descending-price auction each player decides what is her maximal bid, bids it when the auctioneer lower the price to that amount and pays it. That's not different from a first-price sealed-bid auction where bidders have to submit their maximal bids simultaneously, the highest bid wins and is paid by the winner. Both types can be modelled as a sealed-bid first-price auction.
Auctions with perfect information
The following analysis will focus on single-item auctions with rational players obeying the rules, i.e. no collusion.
Second-price sealed-bid auction
- Players
- The n bidders, n ≥ 2.
- Actions
- The set of possible bids bi ≥ 0 is the set of actions of player i.
- Payoff
- For each player i: if bi is the highest bid and bj is the second highest (or the same as the highest but by some deterministic rule decided as the second, e.g. earlier submitted bid is preferred), then player i's payoff is vi - bj, if bi is not the highest bid, then the payoff is 0.
For simplicity let's order the players by their valuation vi so that v1 > v2 > ... > vn > 0.
The action profile (b1, ... , bn) = (v1, 0, ... , 0) is one of many Nash equilibria of this auction. Player 1 bids his price v1 which is the highest and other players bid 0. Player 1 wins the auction and pays 0 (the second highest bid), his payoff is v1. Player 1 can unilaterally change his bid to any value greater than 0 without affecting the outcome. If any other player increases his bid to any value smaller than v1 his payoff won't change. If he bids value higher than v1, he will win the auction but his payoff will be negative. (Resolution of bidding v1 depends on the rule but doesn't change the argument.) No player can therefore improve his payoff by changing his bid.
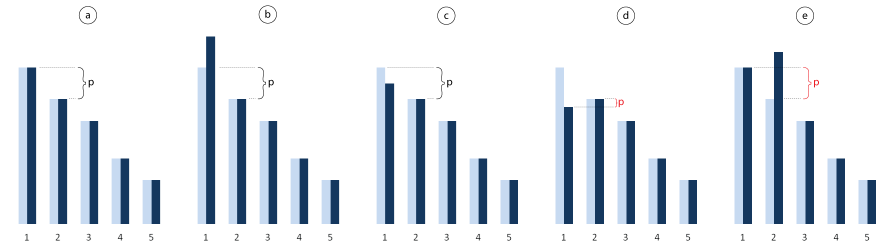
The auctioneer would not like the aforementioned action profile because his revenue would be 0. Let's consider another profile (b1, ... , bn) = (v1, ... , vn), i.e. each player bids her valuation. In this equilibrium the player 1 wins with payoff v1 - b2 (figure 1a). If player 1 raised her bid (figure 1b) or lowered it still above b2 (figure 1c), her payoff wouldn't change (she pays the second price). If she lowered her bid below b2, she would lose and she would be worse off; player 2 would win the auction with negative payoff (figure 1d). If any other player j raised her bid above b1 making it the winning bid, she would have to pay b1 = vj which is less than v2 and her payoff would be negative again (figure 1e).
Exercise 1: Using arguments similar to those above, show that the action profile (b1, ... , bn) = (v2, v1, 0, ... , 0) is an equilibrium. (Solution)
The profile shown in exercise 1 seems less likely than the previous one because player 1 could bid value between v1 and v2 causing the winning player 2 to obtain negative payoff. In second-price sealed-bid auction with perfect information bid bi = vi weakly dominates all other possible bids of player i. Bidding her own evaluation is at least as good as bidding any other value regardless other players' bids. Lowering the bid doesn't change the payoff (in case of winning the auction) but in some cases leads to 0 payoff (losing the auction in situation in which bi = vi would win). Raising the bid doesn't change the payoff in cases when bi = vi is sufficient for winning, but can sometimes cause the player to win and end up with negative payoff. Second-price sealed-bid auction therefore reveals the real price.
First-price sealed-bid auction
- Players
- The n bidders, n ≥ 2.
- Actions
- The set of possible bids bi ≥ 0 is the set of actions of player .i
- Payoff
- For each player i: if bi is the highest bid (on one of the highest and determined to be the winning one by a deterministic rule) then player i's payoff is vi - bi, if bi is not the highest bid, then the payoff is 0.
First-price sealed-bid auction has many Nash equilibria as well but in all of them the winner is player 1 who values the item most highly.
Exercise 2: Show that the profile (b1, ... , bn) = (v2 + ɛ, v2, ... , vn), where ɛ is the smallest possible increment, is a Nash equilibrium. (Solution)
Broadening the argument from exercise 2 leads to the idea that if any player i other than player 1 wins, bi > b1 and if bi > v2 then the payoff of the winning player is negative and losing the auction by bidding 0 is a better decision. If bi < v2 then player 1 can bid higher and win the auction with positive payoff instead of 0.
We can easily see, that a bid bi > vi can be part of an equilibrium but is risky in a similar way as it is in the second-price sealed-bid auction. However a bid bi < vi weakly dominates bi = vi. If bi = vi didn't win the auction lower bid won't win it either and payoff stays 0, but if it won an auction, lower bid can win it too and with greater payoff. In a first-price sealed-bid auction with perfect information bid bi = vi weakly dominates higher bids, but it is weakly dominated by lower bids.
Revenue equivalency of first-price and second-price auctions
We have focused on the optimal strategies of bidders and omitted the interests of the seller - which auction design should he choose in order to maximise his revenue? Surprising thing is that it doesn't matter for single-item private-value auctions due to the revenue equivalency theorem which states that the auction proceeds are the same regardless the precise mechanism (with several assumptions of course). Details of the theorem are beyond the scope of this text, further reading can be found in (Shoham, Leyton-Brown, 2009, pp. 337-340).
Auctions with imperfect information
Auctions discussed in the previous section were not very realistic because we assumed independent private values and perfect information, i.e. each bidder knew valuations of other bidders. By loosening the perfect information requirement we get auctions in which each bidder knows only her private value. Precise analysis of these auctions is rather involved and can be found in (Osborne, pp. 291-295). For this chapter we will show only the basic idea.
Second-price sealed-bid auction
In second-price sealed-bid auction with perfect information we observed that bidding own valuation (bi = vi) weakly dominates any other bid for each player. The same holds true even in the imperfect information scenario! If player i bids her valuation and wins, her payoff is positive (because she pays the second highest bid). When the player knew her valuation was highest she didn't need to bid higher. If she doesn't know it, bidding higher may end up one of three ways:
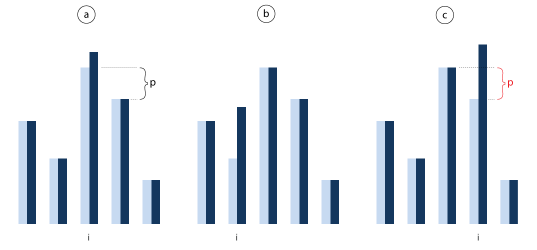
- Her valuation is the highest, even higher bid doesn't change the outcome (figure 2a, compare to figure 1b).
- Her bi > vi is not the highest bid, she still doesn't win (figure 2b).
- Her valuation is lower than other bids (vi < b') but the increased bid is higher (bi > b'). Winning an auction with such a bid makes her payoff vi - b' < 0 (figure 2c, compare to figure 1e).
Overbidding her valuation either doesn't change player's payoff or it leaves her worse off. An argument along the same lines can be made for underbidding her valuation as well. Second-price sealed-bid auction with imperfect information reveals the true valuations because bidding them is weakly dominating strategy for all players.
First-price sealed-bid auction
Coming back to the first-price sealed-bid auction with imperfect information we might expect that bi < v i will weakly dominate higher bids (including bi = vi). Indeed, that is the case. For each player bidding below her own valuation is at least as good as bidding her valuation (which in turn is at least as good as bidding even higher) in an imperfect information scenario.
Overbidding her own valuation is weakly dominated by bidding the valuation in a similar fashion as shown in the previous section. Underbidding the valuation weakly dominates bidding the valuation. While equilibria for this case can be exactly calculated with certain assumptions we won't go into that and settle for a question a rational bidder should ask: Assuming my valuation is the highest, what is the highest of the other players' valuations? I should bid that amount (plus minimal increment), because it still wins but gets me better payoff.
Revenue equivalency in the world of imperfect information
The revenue equivalency theorem mentioned in the section with perfect information still holds true in the world of imperfect information under certain assumptions one of which is risk neutrality. For risk averse players the first-price sealed-bid auction yields greater revenue than the second-price auction.
Auctions with imperfect information and common value component
Auctions with imperfect information and common value component are more realistic but more complicated to analyse as well. The main difference is that valuation of the auctioned item for player i is based not only on his estimate but also on the signals about other players' estimates. Those estimates are partially revealed during the bidding process through bids in open cry auctions, in a sealed-bid auction this doesn't occur.
Consider an auction of mining permits mentioned at the beginning of this chapter. Each player surveys the area and formulates an estimate of the market value on which she will base her bid. However, knowledge of other players' estimates might change her bid - she might see her estimate is too high or too low in comparison to others and adjust it. If all the players put the same weight to their estimate as to the others' estimates, the valuation is purely common and all players will end up with the same valuation (in most auctions this is not the case).

Figure 3 shows number of initial estimates uninfluenced by other players' estimates. Some players are quite close to the real value, some underestimate and some overestimate it. If they had knowledge of other players' estimates (perfect information) all the estimates would converge to an average value (which in this case would be quite accurate). If they didn't have the knowledge and naïvely bid their estimates, then the player who overestimates the real value the most would win and suffer so called winner's curse, i.e. she would win the auction bud with a negative payoff due to overestimating the real value.
In the previous section with private value we observed that in first-price auctions the players bid less than was their valuation. In an auction with a common value component this applies as well, moreover, even players in a second-price auction have an incentive to shade their bids. The winning player is at risk of a negative payoff (which is obviously a preferable outcome for the seller) if she wins the auction because she might be overestimating the real value. More sophisticated bidders try to avoid the winner's curse by strategy similar to shading shown above in the first-price sealed-bid auction.
Things to remember
- Use of auctions isn't limited to selling art but encompasses advertisement systems, government tenders, flowers and virtually anything that can be sold.
- The most important types of auction are English, Dutch, first-price sealed-bid and Vickrey auction.
- Private and common values play important role in analyzing an auction. Private value is appropriate when valuation of the item being sold is independent of other players' valuations (e.g. art), common value is appropriate when the item has some objective value (e.g. natural resources).
- Under certain assumptions all four auction designs can be modelled by the first- and second-price sealed bid auctions.
- Second-price sealed-bid auction reveals true private valuations and gives some information about common valuation.
- Bids are lower in first-price sealed-bid auctions than in second-price sealed-bid auctions but the revenue is the same under certain assumptions - the revenue equivalency theorem.
- There is a risk of the winner's curse in auctions with common value component regardless of the auction mechanism.
Solutions to exercises
Exercise 1
If player 2 bid any value greater than v2, the outcome stays the same. If player 2 bids lower than v2, she loses to player 1 and her payoff is 0. Player 1 would have to increase her bid above v1 to win but her payoff remains 0. Any other player raising her bid below v1 wouldn't change the result and raising it higher would get her negative payoff.
Exercise 2
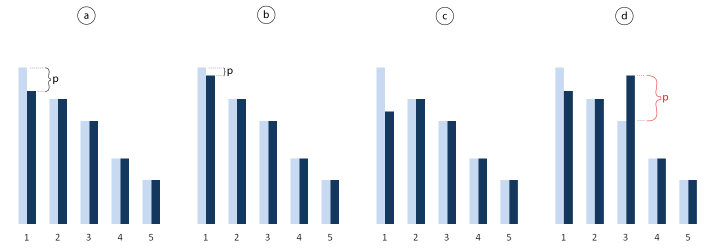
According to the action profile, player 1 wins the auction with payoff v1 - b2 - ɛ (figure 4a). Higher b1 would diminish his payoff (figure 4b), b1 < v2 would mean losing the auction to player 2 with payoff 0 (figure 4c). If any other player increased her bid above v2 + ɛ, she would win with negative payoff (figure 4d) and therefore has no incentive to do so.
References
- DUTTA, Prajit K. Games that we play: introuduction to game theory and it's applications. 2. print. Cambridge, Mass: MIT Press, 1999, pp. 367-382. ISBN 9780262041690.
- GOOGLE. About the ad auction. In: AdSense Help [online], ©2013. [retrieved 2013-01-25.] Available at http://support.google.com/adsense/bin/answer.py?hl=en&answer=160525.
- OSBORNE, Martin J. An introduction to game theory. New York: Oxford University Press, 2003, pp. 79-89, 290-299. ISBN 978-0195128956.
- POLAK, Ben. Game Theory: Lecture 24 - Asymmetric Information: Auctions and the Winner's Curse. In: Yale University: Open Yale Courses [online], 2007. [retrieved 2013-01-25.] Available at http://oyc.yale.edu/economics/econ-159/lecture-24.
- SHOHAM, Yoav, LEYTON-BROWN Kevin. Multiagent systems: algorithmic, game-theoretic, and logical foundations. Cambridge: Cambridge University Press, 2009, pp. 329-381. ISBN 978-0521899437.
- Auction Frequently Asked Questions. U.S. DEPARTMENT OF THE TREASURY, Bureau of the Public Debt. TreasuryDirect® [online], 2012-09-28. [retrieved 2013-01-25.] Available at http://www.treasurydirect.gov/indiv/research/indepth/auctions/res_auctions_faq.htm.