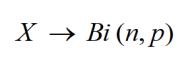Difference between revisions of "Binomial distribution/cs"
| Line 61: | Line 61: | ||
Nyní je čas diskutovat o pravděpodobnostním rozdělení binomické náhodné veličiny. Začneme jednoduchým příkladem a poté se přesuneme k obecnému vzorci. | Nyní je čas diskutovat o pravděpodobnostním rozdělení binomické náhodné veličiny. Začneme jednoduchým příkladem a poté se přesuneme k obecnému vzorci. | ||
==== Příklad Přenosový kanál ==== | ==== Příklad Přenosový kanál ==== | ||
| + | Mějme digitální přenosový kanál, který přenáší 4 bitový signál. Pokusy o přenos jsou nezávislé. Šance, že se jeden bit, který je přenesen přes kanál, přenese s chybou je 0,1. Nechť je [[File:X.png|x15px]] označuje počet bitů s chybou. Určeme [[File:vbr.png|x37px]]. | ||
| + | * Použijme písmeno E pro označení bitu s chybou a písmeno O pro označení bitu bez chyby, tedy přijatého správně. Výsledky tohoto můžeme reprezentovat jako seznam čtyř písmen, která označují bity s chybou a bity bez chyby. Například výsledek OEOE znamená, že druhý a čtvrtý bit jsou s chybou a ostatní dva bity jsou bez chyby. Příslušné hodnoty tedy jsou: | ||
| + | {| class="wikitable" style="margin:auto" | ||
| + | |- | ||
| + | ! Výsledek přenosu !! x !! Výsledek přenosu !! x | ||
| + | |- | ||
| + | | OOOO||0||OEOE||2 | ||
| + | |- | ||
| + | | OOOE ||1 ||EOEO ||2 | ||
| + | |- | ||
| + | | OOEO ||1 ||EOOE ||2 | ||
| + | |- | ||
| + | | OEOO ||1 ||OEEE ||3 | ||
| + | |- | ||
| + | | EOOO ||1 ||EOEE ||3 | ||
| + | |- | ||
| + | | OOEE ||2 ||EEEO ||3 | ||
| + | |- | ||
| + | | OEEO ||2 ||EEOE ||3 | ||
| + | |- | ||
| + | | EEOO ||2 ||EEEE ||4 | ||
| + | |} | ||
| + | * Pro [[File:X.png|x15px]] = 2 je tedy možných 6 výsledků přenosu: {OOEE, OEEO, EEOO, OEOE, EOEO, EOOE} | ||
| + | * Za předpokladu, že jsou pokusy o přenos jednoho bitu nezávislé, je pravděpodobnost možnosti {EEOO}: | ||
| + | [[File:formula1.png|x45px]] | ||
| + | * Také platí, že každý z šesti výsledků, kde [[File:X.png|x15px]]=2, má stejnou pravděpodobnost výskytu a proto | ||
| + | [[File:formula2.png|x35px]] | ||
| + | |||
| + | Nebo všeobecně: | ||
| + | [[File:pxx.png|x15px]] = ''počet možných „úspěšných“ výsledků pro x chyb'' * ''pravděpodobnost každé „úspěšné“ možnosti s výsledkem x chyb a délkou 4'' | ||
| + | * Pro jednoduší odvození můžeme vytvořit tabulku pravděpodobností: | ||
| + | [[File:petj22Tab1.png|x55px]] | ||
| + | * Všimneme si vlastnosti v tabulce: | ||
| + | [[File:petj22Tab2.png|x55px]] | ||
| + | |||
| + | Můžeme zevšeobecnit na: | ||
| + | pravděpodobnost každé „úspěšné“ možnosti s výsledkem [[File:formula3.png|x25px]] | ||
| + | |||
| + | * Ještě nám zbývá odvodit část ''počet možných „úspěšných“ výsledků pro x'', která není na první pohled tak intuitivní. Po krátkém zamyšlení je ale jasné, že se jedná o jednoduchou kombinaci, kdy z množiny [[File:n.png|x12px]] objektů vybíráme počet objektů (x), přičemž nám nezáleží na pořadí. Tedy: | ||
| + | [[File:formula4.png|x40px]] | ||
| + | |||
| + | <ref name="montgomery"></ref> <ref name="bolt"></ref> | ||
| + | |||
| + | ==== Definice ==== | ||
| + | Formalizujme tedy uvedené informace do definice binomického rozdělení: | ||
| + | |||
| + | ===== Podmínky ===== | ||
| + | Náhodný experiment se skládá z [[File:n.png|x12px]] Bernoulliho experimentů tak, že: | ||
| + | # Každý experiment je nezávislý | ||
| + | # Každý experiment má právě dva možné výsledky – „úspěch“ a „neúspěch“ | ||
| + | # Pravděpodobnost „úspěchu“, označována [[File:P2.png|x15px]], pro každý pokus, zůstává konstantní | ||
| + | ===== Vzorec ===== | ||
| + | Náhodná proměnná [[File:X.png|x15px]], která udává počet pokusů s „úspěchem“, má binomické rozdělení s parametry 0<[[File:P2.png|x15px]]<1 a [[File:n.png|x12px]] = 1, 2, … Pravděpodobnostní funkce proměnné [[File:X.png|x15px]] je dána následovně: | ||
| + | [[File:formula5.png|x50px]] | ||
| + | |||
| + | <ref name="bolt"></ref> | ||
| + | |||
| + | == Charakteristiky rozdělení == | ||
| + | Pro odvození střední hodnoty opět využijeme intuitivního příkladu: | ||
| + | Jak nám je již známo, pravděpodobnost mít krevní skupinu typu B je 0,1. Nebo tedy jinými slovy, zhruba 10 % populace má krevní skupinu B. | ||
| + | Předpokládejme, že náhodně vybereme 120 lidí. Kolik lidí můžeme očekávat, že bude mít krevní skupinu typu B? | ||
| + | Odpověď, 12, se zdá být zřejmá. Automaticky jsme vynásobili počet lidí - 120, pravděpodobností výskytu krevního typu B – 0,1. | ||
| + | Z toho jednoduchého příkladu můžeme začít odvozovat. | ||
| + | <ref name="bolt"></ref> | ||
| + | |||
| + | === Střední hodnota === | ||
| + | Pokud je [[File:X.png|x15px]] binomická náhodná veličina s parametry [[File:n.png|x12px]] a [[File:P2.png|x15px]], pak střední hodnota (očekávaná hodnota) [[File:X.png|x15px]] je: | ||
| + | |||
| + | [[File:formula6.png|x30px]] | ||
| + | === Rozptyl === | ||
| + | Rozptyl je na odvození méně intuitivní, ale ne nemožný. Nicméně je tato problematika odvození mimo rámec této kapitoly, a proto ho uvedeme jenom jako vzorec: | ||
| + | |||
| + | [[File:formula7.png|x30px]] | ||
| + | |||
| + | Pro příklad s krví by to tedy znamenalo: | ||
| + | |||
| + | [[File:formula8.png|x30px]] | ||
| + | |||
| + | V náhodném vzorku 120 lidí bychom očekávali přibližně 12 osob s krevním typem B, s odchylkou přibližně 3,3. | ||
= Citace = | = Citace = | ||
<references/> | <references/> | ||
Revision as of 22:39, 1 June 2023
Přemýšleli jste někdy o tom, jak předpovědět počet úspěchů v sérii nezávislých pokusů? Nebo jste možná zvědaví na pravděpodobnost dosažení konkrétního výsledku v sekvenci otázek s odpověďmi ano/ne? Pokud ano, hovoříme v podstatě o binomickém rozdělení, které se vztahuje k binomickým experimentům (tj. s binárními výsledky). Binomické rozdělení je důležitým konceptem v oblasti datové vědy a často se používá v rámci podnikových aplikací.
Úvod
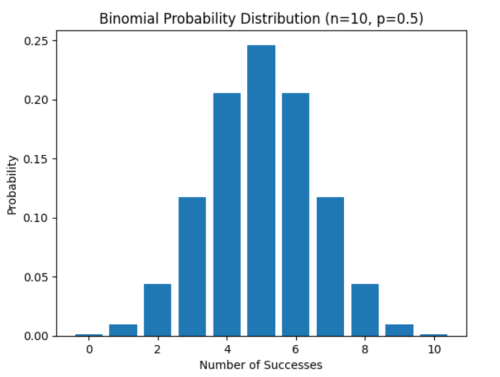
Přemýšlejme o následujících experimentech a náhodných veličinách:
- Házíme 10krát mincí. Označme
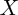 počet kolikrát padne orel.
počet kolikrát padne orel. - Stroj vyrábí díly a některé z nich jsou vadné. Označme
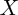 jako počet vadných dílů ze 100 z nich náhodně vybraných.
jako počet vadných dílů ze 100 z nich náhodně vybraných. - Z celkového počtu pacientů trpících konkrétním onemocněním 35 % zažije zlepšení díky určitému léku. U následujících 1000 pacientů, kterým je podán ten samý lék, označme
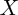 jako počet pacientů, kteří zpozorují zlepšení.
jako počet pacientů, kteří zpozorují zlepšení. - Test obsahuje 10 otázek s více možnými odpověďmi, každá s čtyřmi možnostmi, a vy hádáte u každé otázky. Označme
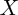 jako počet správně zodpovězených otázek.
jako počet správně zodpovězených otázek.
Každý z těchto náhodných experimentů si lze představit jako soubor opakovaných náhodných pokusů: 10 hodů mincí nebo třeba 1000 pacientů užívajících lék. Náhodná veličina ![]() je počet pokusů, které splňují určité kritérium. Výsledek každého pokusu buď splňuje kritérium, nebo ne; proto lze každý pokus shrnout jako „úspěch“ nebo „neúspěch“. Například v experimentu s testem je pro každou otázku pouze jedna kombinace možností, která je správná, a tedy považována za úspěch.
je počet pokusů, které splňují určité kritérium. Výsledek každého pokusu buď splňuje kritérium, nebo ne; proto lze každý pokus shrnout jako „úspěch“ nebo „neúspěch“. Například v experimentu s testem je pro každou otázku pouze jedna kombinace možností, která je správná, a tedy považována za úspěch.
Termíny „úspěch“ a „neúspěch“ jsou pouze označení. V případě experimentu 2 je vyrobení vadného dílu označováno jako „úspěch“, protože ![]() počítá vadné díly. Stejně dobře můžeme použít označení „A“ a „B“ nebo „0“ a „1“. [1] [2]
počítá vadné díly. Stejně dobře můžeme použít označení „A“ a „B“ nebo „0“ a „1“. [1] [2]
Terminologie
Binomický experiment
Nebo také Bernoulliho experiment/Bernoulliho schéma jsme si v úvodu představili, pojďme si ho nadefinovat a formalizovat.
Požadavky
Požadavky pro to, aby náhodný experiment byl binomickým experimentem, jsou následující:
- Pevný počet (
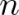 ) pokusů.
) pokusů. - Každý pokus musí být nezávislý na ostatních. (výsledek jednoho pokusu nemá žádný vliv na výsledek ostatních pokusů.)
- Každý pokus má právě dva možné výsledky, nazývané "úspěch" (výsledek, který nás zajímá) a "neúspěch".
- Existuje konstantní pravděpodobnost (pravděpodobnost, že pokus skončí „úspěchem“, je stejná v každém z pokusů) (
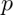 ) úspěchu pro každý pokus, přičemž doplňkem této pravděpodobnosti je pravděpodobnost „neúspěchu“, která se někdy označuje jako
) úspěchu pro každý pokus, přičemž doplňkem této pravděpodobnosti je pravděpodobnost „neúspěchu“, která se někdy označuje jako 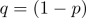 .
.
Náhodná veličina
Pro definici binomického rozdělení začneme s definicí náhodné veličiny ![]() . Tu lze jednoduše definovat jako číselné vyjádření výsledku náhodného jevu.
. Tu lze jednoduše definovat jako číselné vyjádření výsledku náhodného jevu.
Binomická náhodná veličina
V binomických náhodných experimentech je počet „úspěchů“ v n pokusech náhodný. Může nabývat celočíselných hodnot od 0, pokud všechny pokusy skončí „neúspěchem“, nebo může být tak vysoký jako je ![]() , pokud všechny pokusy skončí „úspěchem“.
Náhodná proměnná
, pokud všechny pokusy skončí „úspěchem“.
Náhodná proměnná ![]() , která reprezentuje počet „úspěchů“ v těchto
, která reprezentuje počet „úspěchů“ v těchto ![]() pokusech, se nazývá binomická náhodná veličina a je určena hodnotami
pokusech, se nazývá binomická náhodná veličina a je určena hodnotami ![]() a
a ![]() .
.
Definice
Binomická náhodná veličina ![]() je definována jako počet výskytu události (úspěchů) v
je definována jako počet výskytu události (úspěchů) v ![]() Bernoulliho pokusech.
To, že má náhodná veličina binomické rozdělení zapisujeme: [4]
Bernoulliho pokusech.
To, že má náhodná veličina binomické rozdělení zapisujeme: [4]
Příklad: Binomické nebo ne?
Zvažme ještě několik náhodných experimentů.
U každého z nich rozhodneme, zda je náhodná proměnná binomická. Pokud je, určíme hodnoty pro ![]() a
a ![]() . Pokud není, vysvětlíme proč.
. Pokud není, vysvětlíme proč.
- Příklad A
- Házíme spravedlivou kostkou 50krát;
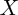 je počet krát, kdy padla šestka.
je počet krát, kdy padla šestka. 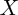 je binomická s
je binomická s 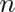 = 50 a
= 50 a 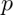 = 1/6.
= 1/6.- Příklad B
- Opět házíme spravedlivou kostkou,
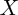 je počet hodů potřebných k dosažení šestky.
je počet hodů potřebných k dosažení šestky. 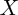 není binomická, protože počet pokusů není pevně stanovený.
není binomická, protože počet pokusů není pevně stanovený.- Příklad C
- Vybíráme náhodně 3 karty jednu po druhé, nevracíme je zpátky do balíčku, z klasické sady obsahující 4 druhy karet.
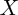 je počet vybraných karet se znakem srdce.
je počet vybraných karet se znakem srdce. 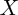 není binomická, protože výběry nejsou nezávislé. (Pravděpodobnost úspěchu (
není binomická, protože výběry nejsou nezávislé. (Pravděpodobnost úspěchu (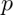 ) není konstantní, protože je ovlivněna předchozími výběry.)
) není konstantní, protože je ovlivněna předchozími výběry.)- Příklad D
- Odpovídáme na 10 testových otázek zcela náhodně, prvních pět otázek je ano/ne a druhých pět otázek má čtyři možnosti, ze kterých je jedna správná.
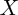 představuje počet správných odpovědí.
představuje počet správných odpovědí. 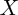 není binomická, protože pravděpodobnost
není binomická, protože pravděpodobnost 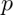 se mění z 1/2 na 1/4.
se mění z 1/2 na 1/4.- Příklad E
- Pravděpodobnost mít krevní skupinu B je 0,1. Vybíráme 4 náhodné osoby.
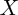 je počet osob s krevní skupinou B.
je počet osob s krevní skupinou B. 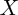 je binomická s
je binomická s 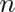 = 4 a
= 4 a 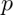 = 0,1.
= 0,1.- Komentář: Při výběru relativně malé náhodné vzorky (4 osoby) z velké populace, i když se odběr provádí bez „náhrady“, můžeme předpokládat nezávislost, protože matematický vliv odstranění jednoho jedince z velké populace na další výběr je zanedbatelný.
Binomické pravděpodobnostní rozdělení
Nyní je čas diskutovat o pravděpodobnostním rozdělení binomické náhodné veličiny. Začneme jednoduchým příkladem a poté se přesuneme k obecnému vzorci.
Příklad Přenosový kanál
Mějme digitální přenosový kanál, který přenáší 4 bitový signál. Pokusy o přenos jsou nezávislé. Šance, že se jeden bit, který je přenesen přes kanál, přenese s chybou je 0,1. Nechť je ![]() označuje počet bitů s chybou. Určeme
označuje počet bitů s chybou. Určeme ![]() .
.
- Použijme písmeno E pro označení bitu s chybou a písmeno O pro označení bitu bez chyby, tedy přijatého správně. Výsledky tohoto můžeme reprezentovat jako seznam čtyř písmen, která označují bity s chybou a bity bez chyby. Například výsledek OEOE znamená, že druhý a čtvrtý bit jsou s chybou a ostatní dva bity jsou bez chyby. Příslušné hodnoty tedy jsou:
| Výsledek přenosu | x | Výsledek přenosu | x |
|---|---|---|---|
| OOOO | 0 | OEOE | 2 |
| OOOE | 1 | EOEO | 2 |
| OOEO | 1 | EOOE | 2 |
| OEOO | 1 | OEEE | 3 |
| EOOO | 1 | EOEE | 3 |
| OOEE | 2 | EEEO | 3 |
| OEEO | 2 | EEOE | 3 |
| EEOO | 2 | EEEE | 4 |
- Pro
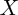 = 2 je tedy možných 6 výsledků přenosu: {OOEE, OEEO, EEOO, OEOE, EOEO, EOOE}
= 2 je tedy možných 6 výsledků přenosu: {OOEE, OEEO, EEOO, OEOE, EOEO, EOOE} - Za předpokladu, že jsou pokusy o přenos jednoho bitu nezávislé, je pravděpodobnost možnosti {EEOO}:
Nebo všeobecně:
![]() = počet možných „úspěšných“ výsledků pro x chyb * pravděpodobnost každé „úspěšné“ možnosti s výsledkem x chyb a délkou 4
= počet možných „úspěšných“ výsledků pro x chyb * pravděpodobnost každé „úspěšné“ možnosti s výsledkem x chyb a délkou 4
- Pro jednoduší odvození můžeme vytvořit tabulku pravděpodobností:
- Všimneme si vlastnosti v tabulce:
Můžeme zevšeobecnit na:
pravděpodobnost každé „úspěšné“ možnosti s výsledkem ![]()
- Ještě nám zbývá odvodit část počet možných „úspěšných“ výsledků pro x, která není na první pohled tak intuitivní. Po krátkém zamyšlení je ale jasné, že se jedná o jednoduchou kombinaci, kdy z množiny
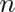 objektů vybíráme počet objektů (x), přičemž nám nezáleží na pořadí. Tedy:
objektů vybíráme počet objektů (x), přičemž nám nezáleží na pořadí. Tedy:
Definice
Formalizujme tedy uvedené informace do definice binomického rozdělení:
Podmínky
Náhodný experiment se skládá z ![]() Bernoulliho experimentů tak, že:
Bernoulliho experimentů tak, že:
- Každý experiment je nezávislý
- Každý experiment má právě dva možné výsledky – „úspěch“ a „neúspěch“
- Pravděpodobnost „úspěchu“, označována
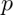 , pro každý pokus, zůstává konstantní
, pro každý pokus, zůstává konstantní
Vzorec
Náhodná proměnná ![]() , která udává počet pokusů s „úspěchem“, má binomické rozdělení s parametry 0<
, která udává počet pokusů s „úspěchem“, má binomické rozdělení s parametry 0<![]() <1 a
<1 a ![]() = 1, 2, … Pravděpodobnostní funkce proměnné
= 1, 2, … Pravděpodobnostní funkce proměnné ![]() je dána následovně:
je dána následovně:
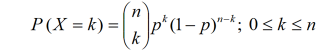
Charakteristiky rozdělení
Pro odvození střední hodnoty opět využijeme intuitivního příkladu: Jak nám je již známo, pravděpodobnost mít krevní skupinu typu B je 0,1. Nebo tedy jinými slovy, zhruba 10 % populace má krevní skupinu B. Předpokládejme, že náhodně vybereme 120 lidí. Kolik lidí můžeme očekávat, že bude mít krevní skupinu typu B? Odpověď, 12, se zdá být zřejmá. Automaticky jsme vynásobili počet lidí - 120, pravděpodobností výskytu krevního typu B – 0,1. Z toho jednoduchého příkladu můžeme začít odvozovat. [3]
Střední hodnota
Pokud je ![]() binomická náhodná veličina s parametry
binomická náhodná veličina s parametry ![]() a
a ![]() , pak střední hodnota (očekávaná hodnota)
, pak střední hodnota (očekávaná hodnota) ![]() je:
je:
Rozptyl
Rozptyl je na odvození méně intuitivní, ale ne nemožný. Nicméně je tato problematika odvození mimo rámec této kapitoly, a proto ho uvedeme jenom jako vzorec:
Pro příklad s krví by to tedy znamenalo:
V náhodném vzorku 120 lidí bychom očekávali přibližně 12 osob s krevním typem B, s odchylkou přibližně 3,3.
Citace
- ↑ 1.0 1.1 1.2 KUMAR, Ajitesh Binomial Distribution Explained with Examples [online]. 2023 [cit. 2023-06-01] Dostupné z: https://vitalflux.com/binomial-distribution-defined-with-10-examples/
- ↑ 2.0 2.1 MONTGOMERY, Douglas C. Applied Statistics and Probability for Engineers [online]. 2011 [cit. 2023-06-01] Dostupné z: https://industri.fatek.unpatti.ac.id/wp-content/uploads/2019/03/088-Applied-Statistics-and-Probability-for-Engineers-Douglas-C.-Montgomery-George-C.-Runger-Edisi-5-2011.pdf
- ↑ 3.0 3.1 3.2 3.3 3.4 UF Health Binomial Random Variables [online]. 2014 [cit. 2023-06-01] Dostupné z: https://bolt.mph.ufl.edu/6050-6052/unit-3b/binomial-random-variables/
- ↑ VŠB DISKRÉTNÍ ROZDĚLENÍ PRAVDĚPODOBNOSTI [online].[cit. 2023-06-01] Dostupné z: https://homel.vsb.cz/~dom033/predmety/statistika/ucebni_text/7DNV.pdf