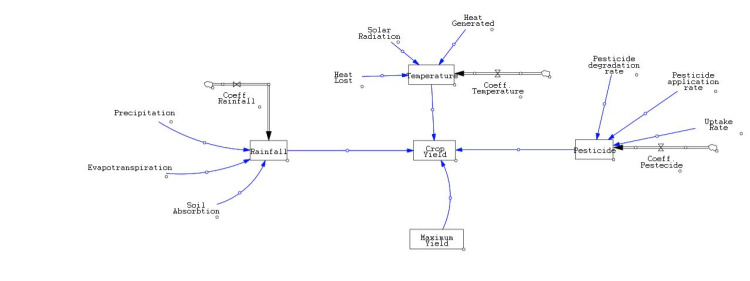
Cropyield
Introduction Crop growth and development simulations and yield forecasting will be performed using variables such as crop type, planting date, soil type, soil texture, and climate data (temperature, rainfall, etc.) Problem definition Arable land is increasingly limited, while the world's population has steadily been increasing over the years. To meet rapidly rising demand, production must be increased while natural resources must be protected. Predicting crop yield under different conditions, such as changing temperature, varying rainfall, use of pesticides and maximum yield of the specific farmland, has become critical for farmers and other stakeholders who use these predictions to make more informed decisions about how to allocate resources, such as labor, equipment, and inputs, to maximize yield and productivity. Model This simulation was conducted using Vensim. I used the following stock variables, and equations;
- Crop yield:
The expected yield per hectare of crops planted during the planting season. (Rainfall*Pesticide)+(Temperature*Maximum Yield)
- Rainfall:
The rate of change of rainfall which is equal to the precipitation received by the crops (P) minus the evapotranspiration of the crops (ET) minus the infiltration rate of water into the soil (Inf). The infiltration rate of water into the soil is a measure of how much water is able to enter the soil "Coeff. Rainfall"*(Precipitation-Evapotranspiration-Soil Absorption)
- Temperature:
The rate of change of temperature which is equal to the solar radiation received by the crops (S) minus the heat lost by the crops through evapotranspiration and radiation plus the heat generated by the crop growth and respiration. "Coeff. Temperature"*(Heat Generated+(Solar Radiation-Heat Lost))
- Pesticide:
the rate of change of pesticide concentration in the soil is equal to the rate at which the pesticide is being added to the soil (R) minus the rate at which it is being taken up by the crops (U) and the rate at which it is degrading in the soil (D). "Coeff. Pestecide"*(Pesticide application rate-Uptake Rate-Pesticide degradation rate)
- Maximum yield:
The historic maximum amount of crop yield in tons per hectare of a specific planting area which is a constant between 5 to 10 tons/hectares
Results Based on the model, we can see that rainfall, temperature and pesticides have a direct impact on crop yield. When I simulated low temperature, the crop yield dropped, and vice-versa, when high or low levels of rainfall were simulated, the crop yield rose and dropped accordingly. Equally the use of pesticides has a direct impact on the yield of the crop, as its absorption by the plants drastically increase the yield of the crop.
Conclusion This simulation clearly shows that when any one of the stock variables are reduced, this affects the yield of the crop for that planting season. Therefore, when we have low rainfall, stakeholders can take measures to increase the use of pesticides, or employ other methods like irrigation to simulate rainfall and increase crop yield. In situations where there is abundant rainfall, less pesticides can be used