Teorie her/cs
Contents
Úvod
Teorie her je jedna z disciplín aplikované matematiky zabývající se komplexními systémy. Těmi jsou konfliktní situace (“hry”) mezi několika různými stranami (“hráči”) [1].
K popisu rozhodovacího procesu několika osob během jedné hry je převážně využíván matematický aparát, avšak v některých situacích se kvůli komplexnosti těchto systémů musíme spolehnout pouze na empirické (simulační) řešení, neboť ne vždy musí analytické řešení být k dispozici [1].
Co je to “hra”?
Základním myšlenkou hry je tatáž, či velmi podobná té, jakou si představíme u společenských her [2].
Po vypuknutí hry můžeme definovat posloupnosti kroků/tahů, kterými hráči hrají danou hru [2]. V rámci každého tahu hráči vybírají, jakými kroky ze všech jim dostupných se budou ubírat [2]. Tato volba může být v některých problémech omezena či upravena náhodou (hodem kostky, zamícháním balíčku karet atd.). Klasickým příkladem her jsou šachy, ve kterých náhoda nehraje žádnou roli (kromě rozlosování toho, kdo začne jako první), bridge, ve kterém náhoda sice již ovlivňuje hru, ale zkušenosti a um jsou stále důležité, a ruleta, při které jde jen o náhodu a umění v ní nehraje žádnou roli [2].
Na rozdílu šachů a bridge můžeme popsat ještě jeden z důležitých faktorů her [2]. V šachách všichni hráči vědí, jaké všechny kroky předcházeli aktuálnímu stavu hry, zatímco u bridge tuto znalost nemáme. Tedy v některých hrách může nastat situace, že nevíme, jaký z možných tahů soupeř zahrál [2]. Pokud chce hráč zakládat rozhodování na hře ostatních hráčů, ne vždy může mít k dispozici všechny informace, a tedy nemusí vědět, v jakém přesném stavu se hra právě nachází [2]. Na základě kompletnosti dostupných informací hráčů dělíme hry na hry s úplnými a neúplnými informacemi.
Na konci hry ještě běžné probíhá nějaké vyhodnocení. Vítězný hráč bývá odměněn, ať už ve formě peněz, prestiže, nebo zadostiučinění [2].
Co je to “strategie”?
Strategií se v teorii her myslí samotný algoritmus, podle kterého se v každém stavu hry rozhodneme, jaký krok provedeme [3][4], proto se také těmto strategiím přidává přívlastek rozhodovací.
Rozhodovací strategie dále můžeme dělit dle toho, jak pracují se ziskem v dané hře. Pokud se hráč bude rozhodovat podle strategie, která maximalizuje očekávaný zisk, tak této strategii říkáme optimální [4]. Pokud pro daného hráče v dané hře existuje strategie, která je optimální nehledě na tahy ostatních hráčů, říkáme této strategii dominantní, popř. ryzí [5].
V některých typech her však může být významným prvkem náhoda, popř. nedostatek informací, pak velmi často nastává situace, že dominantní strategie neexistuje (kámen-nůšky-papír). V těchto případech se využívá pravděpodobnostního ohodnocení jednotlivých možných stavů a následných odměn. Těmto strategiím se pak říká pravděpodobnostní nebo také smíšené [1].
O strategii více pojednává článek Rozhodovací strategie.
Historie
Starověk
První příklad z teorie her se dá najít již ve starověké Babylonii, a to v Babylonském Talmudu [6]. Babylonský Talmud byl soupisem starověkého práva a obyčejů, sepsaný během prvních pár století našeho letopočtu, a slouží jako základ Židovského náboženství, trestního a občanského práva. V něm je popsán tzv. “marriage contract problem”, který udává příklady rozdělení jmění muže mezi zbývající ženy po jeho smrti. Mnoha vzdělancům se závěry tohoto problému, popsané v Babylonském Talmudu, zdály nesmyslné a dokázány byly jako možné až v roce 1985, kdy vyšly jako výsledky adekvátně definovaných her [6].
Novověk
Další významná známka o principech teorie her se neobjevuje až do 13. listopadu 1713, kdy James Waldergrave poslal Pierre-Remond de Montmortovi první známé řešení hry dvou hráčů za použití minimax smíšené strategie [6]. Bohužel tuto strategii neaplikoval na žádné další problémy, protože si myslel, že jsou smíšené strategie pro běžné hry pravděpodobně neaplikovatelné [6].
V 19. století se objevuje první náznak Nashova equilibria v práci Augustina Cournota, Mathematical Principles of the Theory of Wealth [6].
Na začátku 20. století se objevují první teorie Teorie her. Tou úplně první je pravděpodobně Zermanova teorie z roku 1913 popisující hru šachy [6].
V letech 1921 a 1927 pracoval Emile Borel na poznání strategických her a definoval první myšlenky smíšených strategií [6].
Konečně, v roce 1928, John von Neumann publikoval článek “Zur Theorie der Gesselschaftsspiele” a tím položil první základy celému oboru matematiky Teorie Her [6] [7].
Typy her
Hry se často dělí na statické/dynamické a s neúplnými/úplnými informacemi.
Statické hry / Jednorázové hry
V rámci statických her zvolí všichni hráči svoji strategii a následně je zjištěno, jaký je výsledek hry [8]. Tyto hry se dají popsat dvěma kroky:
- krok: Všichni hráči si naráz, nezávisle, bez jakékoli komunikace zvolí svůj tah dle své strategie,
- krok: Všichni hráči se zachovají dle své zvolené strategie, je posouzen výsledek hry a rozděleny odměny [8].
Příkladem by mohla být ideální hra kámen-nůšky-papír , kdy hráči naráz zvolí a zahrají svojí strategii (kámen/nůžky/papír), hra je vyhodnocena a vítěz je znám hned.
Samostatný článek o statických hrách
Dynamické hry / Opakované hry
Dynamickými hrami jsou hry, kde probíhá opakované střetnutí strategií hráčů [8]. V podstatě se jedná o mnohokolové statické hry, kde se v 2.kole posoudí pouze dílčí výsledky a jsou rozděleny dílčí odměny, a tyto hry se opakují, dokud není naplněn jejich cíl [8].
Jedná se například o většinu deskových her (Monopoly, Dostihy a sázky, Člověče nezlob se a další).
Samostatný článek o dynamických hrách
Hry s úplnými informacemi
V tomto typu her mají všichni hráči k dispozici stejné znalosti o:
- všech možných krocích ostatních hráčů,
- všech možných výsledcích dané hry,
- co mají všechny možné kombinace možných kroků všech hráčů za výsledek,
- preference zvolení kroků ostatními hráči.
Statické hry s úplnými informaci jsou těmi nejjednoduššími hrami. V praxi se s nimi příliš nepotkáme, ale umožňují nám položit první základy tohoto oboru [8].
Hry s neúplnými informacemi
Hrami s neúplnými informacemi myslíme hry, kde hráči nemají stejné znalosti alespoň o jedné z informací o hře (viz hry s úplnými informacemi).
Například na aukci mají všichni hráči informaci o vyvolávající ceně a minimálním příhozu, ale nevědí, jaké možnosti mají ostatní hráči, kolik mají financí, ani jaký je jejich cíl. [9]
Další dělení
Dalšími možnými děleními jsou dělení na základě počtu hráčů, počtu možných strategií, součtu zisku všech hráčů, dle počtu ekvilibrií a zda hráči spolupracují, či ne.
Zápisy her
Normální forma
Normální forma je maticovým zápisem hry [5]. K použití tohoto zápisu musíme znát množinu všech hráčů, jejich tahů a preferencí [5]. Je vhodný k převážně k zápisu her dvou hráčů (první hráč má strategie ve sloupcích, druhý v řádcích), při větším počtu hráčů se ztrácí přehlednost matic [5]. Výhodou oproti rozšířené formě je snadnost nalezení ekvilibrií [5].
Samostatný článek o normální formě
Rozšířená forma
Rozšířená forma je stromový zápis hry ([[1]] je souvislý, acyklický graf) [5]. Na rozdíl od normální formy umožňuje i zápis her s nekompletními informacemi [5]. Jednotliví hráči jsou rozděleny do různých vrstev grafu [5].
Samostatný článek o rozšířené formě
Pojmenované problémy
Cournotův model
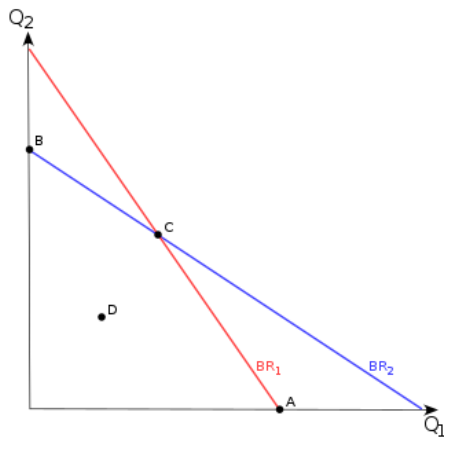
Cournotův model je ekonomický model popisující duopol [5]. V rámci teorie her bychom ji zařadili to statických her s úplnými informacemi (firmy mají stejnou lin. funkci mezních nákladů) [5]. Jedná se o model, kde si firmy konkurují množstvím vyrobených produktů. Pokud všechny firmy správně odhadnou strategii ostatních konkurentů, vzniká v něm tzv. Cournotova rovnováha (podmnožina rovnovah později známých jako Nashovy rovnováhy ) [5].
Grafické znázornění Cournotovy rovnováhy v bodě C (v průsečíku reakčních křivek).
Matching pennies
Jedná se o hru dvou hráčů, ve které hráči 1 a 2 mají minci a tajně na ni zvolí “panna”, nebo “orel”, poté naráz ukáží svůj výběr. Pokud zvolili rozdílné strany, získává obě mince hráč 1, pokud stejné získává je hráč 2[8].
Maticový zápis hry:
Je vidět, že hra nemá ryzí Nashovo ekvilibrium (neexistuje ryzí strategie na nejlepší reakci, nejlepší reakce)[8].
Avšak hra má Nashovo ekvilibrium ve smíšené strategii: kdy každý hráč zvolí každou stranu mince se stejnou pravděpodobností, tím vznikne celkové ekvilibrium, při kterém celkový zisk každého z hráčů je 0[8].
Kámen-nůžky-papír
Jedná se v rámci teorie her o velmi podobou hru k matching pennies , jen s tou změnou, že hra má 3 strategie na místo 2 [8].
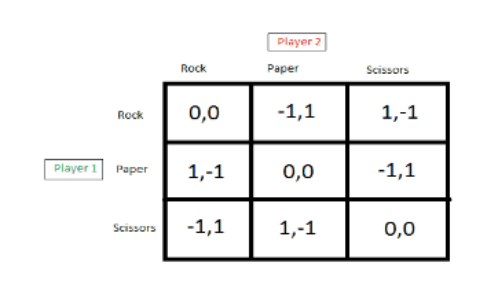
Maticový zápis:
Je opět vidět, že tato hra nemá žádné ryzí Nashovo ekvilibrium.
Nashovo ekvilibrium pro smíšené strategie nastane znovu v případě, že každý z hráčů bude hrát všechny strategie se stejnou pravděpodobností (1/3)[8].
Vězňovo dilema
Hra kuře
Bitva pohlaví
Vickreyova aukce
Článek na téma Vickreyova aukce
Vězňovo dilema (více hráčů)
Článek na téma Vězňovo dilema více hráčů
Literatura
- ↑ 1.0 1.1 1.2 Dlouhý, Martin; Fiala, Petr Úvod do teorie her Oeconomica, 2007. [Cit. 29-05-2022]. ISBN 978-80-245-1273-0
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Owen, Guillermon. Game Theory. Emerald Group Publishing, 2013. [Cit. 29-05-2022]
- ↑ Frieb J, 2007. [online] https://web.archive.org/web/20070221142004/http://www2.ef.jcu.cz/~jfrieb/rmp/data/teorie_oa/TEORIE%20HER.pdf [Cit. 29-05-2022].[Arch. 21-02-2007].
- ↑ 4.0 4.1 Nust.na. 2022. [online] https://www.nust.na/sites/default/files/documents/MEN311S-2016-UNIT%207%20(GAME%20THEORY%20AND%20STRATEGIC%20DECISION%20MAKING).pdf [Cit. 29-05-2022]
- ↑ 5.00 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 Fudenberg, Drew; Tirole, Jean. Game Theory. MIT Press, 1991. [Cit. 29-05-2022]
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 Walker, Paul. An Outline of the History of Game Theory. 1995. Doi: 10.22004/ag.econ.263767
- ↑ Tucker, William Albert; Luce, Duncan Robert. Contributions to the Theory of Games. Volume 4. Princeton University Press, 1959. [Cit. 29-05-2022]
- ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9 Tadelis, Steven. Game Theory: An Introduction. Princeton University Press, 2013. [Cit. 29-05-2022]
- ↑ Levin, Jonathan. Games of Incomplete Information. 2002. [online] https://web.stanford.edu/~jdlevin/Econ%20203/Bayesian.pdf [Cit. 29-05-2022]