Nash equilibrium
Nash equilibrium is a fundamental concept in the game theory defined by John Nash in 1950s and it is highly used method of predicting the outcome of a strategic interaction in the social sciences. [1]
Contents
Games in strategic form
To define Nash equilibrium, we have to define one of the most widely used mathematical model of game theory, game in strategic (also called normal) form. Game in the strategic form is a model of interacting decision-makers. In the game theory, the decision-makers are very often called players. Each player in the strategic game has a set of possible actions and preferences about the action profile, which is list of all possible actions of all players. You can find more about strategic or normal form at Normal form page.
To define it more precisely, strategic game consist of:[2]
- a set of players Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
- for each player, a set of actions (or strategies) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
- for each player, preferences Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i} (or payoffs) over the set of action profiles Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a}
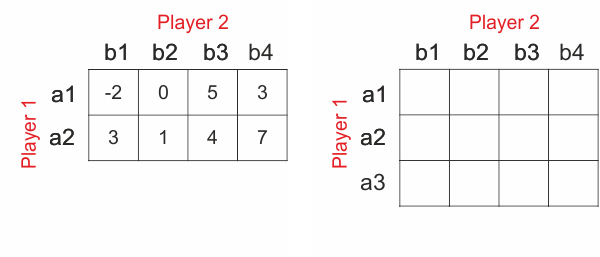
Games in strategic form are very often represented by payoff (or we can say table) like this one below.
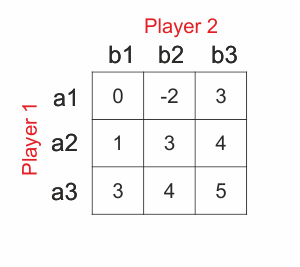
In this matrix Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} are actions of player 1 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_i} are actions of player 2. Numbers inside the matrix are payoffs of player 1 in case of selected actions. Now we can show, how both players will progress in case of searching best action (strategy).
Dominant strategies
If we look at the matrix above, we can see that player one will never choose action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1}
(of course in case, he is rational, which is expected). This is because all payoffs in first row are smaller than payoffs in second row. Also player two won´t choose action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_3}
because all payoffs in this column are smaller than in other two columns.(Payoffs of Player 2 are -(payoffs) of Player 1). So we can delete it with clear conscience.[3] This situation is showed in the picture below.
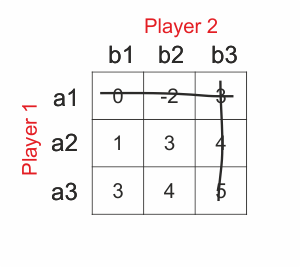
Now only two strategies left for both players. If we look precisely at the strategy of Player 1 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2}
, we can see, that payoffs are smaller again than in strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_3}
. The same situation is with Player 2 and his Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_2}
strategy. So we can delete strategies again.
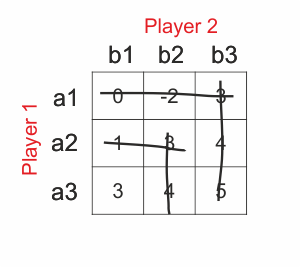
Dominant strategy is strategy where all payoffs are higher than equivalent payoffs in other strategy of one player.[4]
In our case, we found solution by gradual elimination of dominated strategies. But what to do, when we can´t find solution this way? We can use Nash equilibrium.
But before we use Nash equilibrium, let´s practice dominant and dominated strategies.
Exercise 0
- Try to find solution in the first matrix using gradual elimination of dominated strategies
- Fill in the second matrix such payoffs to rational Player 1 choose strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1}
and Player 2 strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_4}
Definition of Nash equilibrium
Now We can define Nash equilibrium as an action profile Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a*} with the property that no player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} can do better by choosing an action different from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a*_i} , given that every other player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j} adheres to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a^*_j} .[2]
Or to be absolutely exact:
Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a}
be an action profile, in which the action of
each player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a'_i}
be any action of player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
(either equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
, or different from it). Then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a'_i , a_-_i)}
denotes the action profile in which every player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j}
except
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
chooses her action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_j}
as specified by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a}
, whereas player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
chooses Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a'i}
. (The Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -i}
subscript on a stands for except Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
.) That is, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a'_i , a_-_i)}
is the action profile in which
all the players other than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
adhere to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a}
while Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
deviates to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a'_i}
. (If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a'_i = a_i}
then
of course Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a'_i , a_-_i) = (a_i, a_-_i) = a}
).
The action profile Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a^*}
in a strategic game with ordinal preferences is a Nash equilibrium
if, for every player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
and every action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
of player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a*}
is at least as good according
to player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
's preferences as the action profile (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a^*_i}
) in which player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
chooses Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
while every other player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle j}
chooses Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_j}
.
Equivalently, for every player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i(a^*)>= u_i(a_i , a^*_-_i)}
for every action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i}
of player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
,
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i}
is a payoff function that represents player i's preferences.[2]
In own words, Nash equilibrium is such solution, that you cannot do any better by choosing different one, when other player remains faithful to this solution.
Now we know, what Nash equilibrium is, so let´s find out, how to find it.
Nash equilibrium and zero sum games
| Who was Jonh F. Nash |
|---|

|
| John Forbes Nash was born on June 13, 1928 in Bluefield as a son of electrical engineer (father) and teacher (mother). He attended standard schools in Bluefield. His parents bought him an encyclopedia, which started his interest in science. By the time he was student at the high school, he was reading Men of Mathematics by E.T.Bell and he also did some chemistry and electrical experiments. He prepared for career of electrical engineer like his father, but finally he became a chemistry student at Carnegie University in Pittsburgh. But he was ´t satisfied with his studies, because as he said, it was more about how well one could handle pipette, than how well one understand and leatn facts. So he moved to the mathematics faculty and studied and graduated there. After his graduation, he had been offered to study at either Harvard or Princeton. And it was Princeton, which became his next study location. It was Princeton, where he wrote his dissertation thesis about game theory an determined some properties, which was subsequently called Nash equilibrium.
After that, he worked as instructor at M.I.T. at the mathematics faculty, where he studied problems involving partial differential equations. He entered to the marriage in 1957 and in 1959 he was psychiatrically diagnosed as schizophrenic. As a consequence, he left M.I.T and after 50 days in hospital, he traveled to Europe and tried to gain status there as a refugee. After that he was hospitalized in New Jersey. But he recovered and now, as he said, he thinking rationally again. In 1994 he received Nobel Memorial Prize in Economic Sciences as a result of his dissertation on Princeton. [5] |
Zero sum games are games in the game theory, where one player loses what second wins or vice versa. It is one of the simplest game model. As was said, it could be represented by payoff matrix.
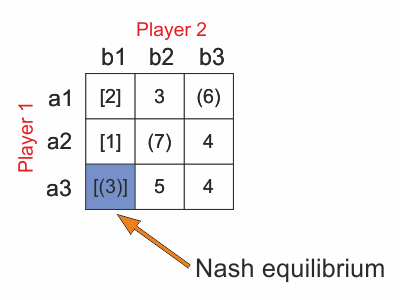
To find Nash equilibrium, we have to find steady state first. In zero sum games, the steady state is the element in the payoff matrix, which is the highest in the column and also the smallest in the row. This is because second player tries to minimize payoff of player 1, because first player payoff is -(payoff ) of second player. [3]
In our matrix, we found the steady state (element 3). It means that this game represented by payoff matrix has pure Nash equilibrium, which is action pair (a3,b1). So the Player 1 will choose action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_3} and Player 2 action Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_1} . There could be more steady states in the game represented by matrix, or none. Does it mean, that there is no Nash equilibrium? Not really. If there is not steady state, than the game doesn´t have pure Nash equilibrium but Nash equilibrium is in mixed strategies. In case of more steady states than one with same value, the game has alternative Nash equilibria. [3]
We will find out more about mixed strategies after a while. Now let´s do some practise.
exercise 1
- Find steady state and pure Nash equilibrium if there is any.
- Fill in the payoffs into the matrix
- so as game has one steady state and pure Nash equilibrium
- so as game has more than one steady state and has alternative Nash equilibria
Mixed strategies
As mentioned above if we cannot determine steady state, than there is no pure Nash equilibrium but Nash equilibrium is in mixed strategies. That means that we cannot precisely determine which actions will players choose but we can identify probability distribution over player´s actions (strategies). [3]
| To get Nash equilibrium in mixed strategies, we can also solve dual linear task, which is related to the maximization task listed above. Because results are equivalent and to solve dual task is more complicated, only primal task is demonstrated.
If you are interested, you can find more about linear programming at [1] |
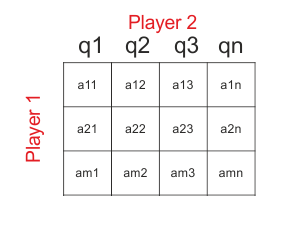
Generally speaking, we can define probability, that player one or two will choose the action. To determine this probability distribution is more complicated. We have to solve maximization task using linear programming methods:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle maximize:}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q_1 + q_2+.....+q_n}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle s.t.:}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1_1*q_1+a_1_2*q_2+.....+a_1_n*q_n <= 1}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ...}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ...}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_m_1*q_1+a_m_2*q_2+.....+a_m_n*q_n <= 1}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q_j>=0; j=1,2,....,n}
where q1...qn are variables and a11...amn are individual payoffs for combination of actions. This task can be solved using Excel, Lingo or manually by simplex method.
Nash equilibrium and non zero sum games
Non zero sum game are little bit more complex than zero sum games. Unlike the zero sum games, payoffs of one player are not dependent on second player´s payoffs. That means Players try to maximize their own profit. As a mathematical representation of this kind of game, we can also use matrix. But this matrix is little bit different, because there are payoffs of both players in it.
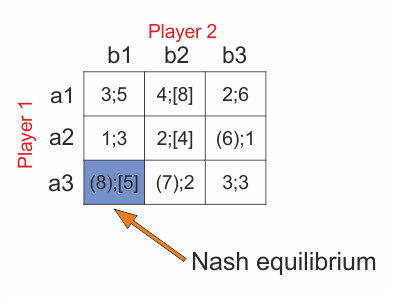
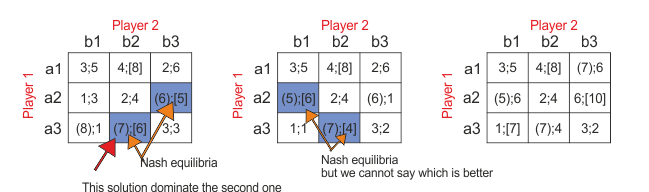
The first number in the cell is payoff of Player 1 and the second one is payoff of Player 2. To determine Nash equilibrium, we have to find maximum value in the columns for first player and maximum value in the rows for second player. This is because both players try to maximize their profit based on second player´s choice.[3]
In this matrix, we can find one pure Nash equilibrium, which is action pair (a3, b1).
As same as in zero sum game, there are three possibilities, that may occur. We can determine one pure Nash equilibrium, more than one or none. If there is more than one Nash equilibrium and one of them dominates (either payoffs are higher (or one payoff is the same) then payoffs in other Nash equilibrium) others, than players will choose this solution, because is better for both players. If there is more than one Nash equilibrium and no one of them dominates others, than we can´t determine solution to choose. The last possibility is that there is no pure Nash equilibrium in the game. In this case, we have to find Nash equilibrium in mixed strategies.
exercise 2
- Find pure Nash equilibrium if there is any.
Nash Equilibrium decision problems
Sometimes things aren't so clear and Nash equilibrium didn't ´t get sufficient solution in strategic games, so let´s show some examples of well-known games in strategic form.
Prisoner´s dilemma
The Prisoner's dilemma is one of the most well-known strategic games. It was researched many times and many ways due to huge variety of situations in real life which is similar to this problem.
The definition of Prisoner´s dilemma
There are two suspects in a major crime situated in separate cells. We have enough evidence to convict each of them of a minor offense, but we can´t convict either of them of the major crime unless one of them pleads guilty and tells information that help to find the second one guilty. If they both say nothing (cooperate), each will be convicted of the minor offense and spend one year in jail. If one and only one of them betrays other, than he will be set free and used as a witness. The other one will spend four years in jail. If they both betray, they will spend three years in jail. [2]
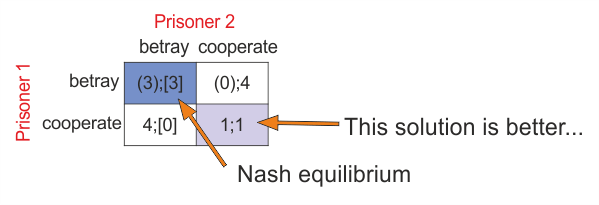
We can demonstrate this situation as shown above. Payoffs in the matrix represent years in prison (higher values are worse). When we try to find Nash equilibrium, we get pair of action (betray,betray), but as we can see that isn´t the best solution. The Best solution is (cooperate, cooperate). This example shows, that Nash equilibrium is not always Pareto-effective.
Bach or Stravinsky (also known as battle of sexes)
Two people decided to go out together to a concert of music by either Bach or Stravinsky. However, one person prefers Stravinsky and the other person prefers Bach. [4]
The situation is represented using payoff matrix below.
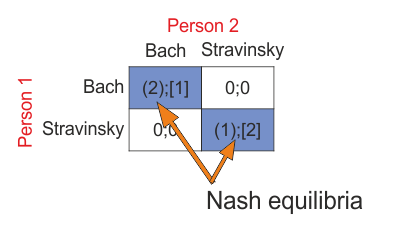
Battle of sexes represent situation, when two people want to spend time together, but they have different preferences. In this case we found two Nash equilibria, but we still don´t know how to play. Either of them will have to yield.
Coordination game
Now imagine almost same situation as above, but they both prefer Bach to Stravinsky. Situation is listed below.
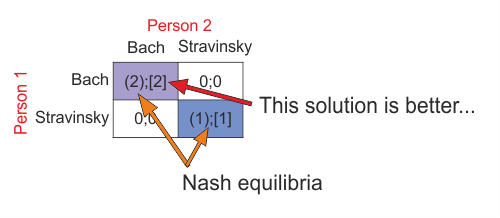
In this situation we get also two Nash equilibria. However one (Bach, Bach) is noticeably better than other, notion of Nash equilibrium doesn´t eliminate the second one (Stravinsky, Stravinsky) . [4]
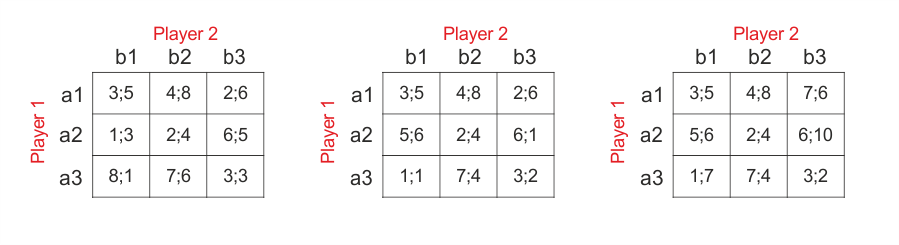
Solutions to the exercises
Exercise 0
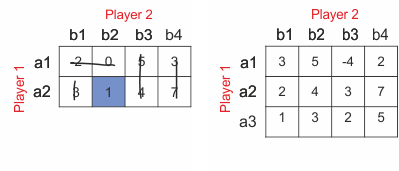
Exercise 1a
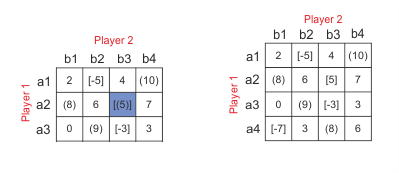
Exercise 1a
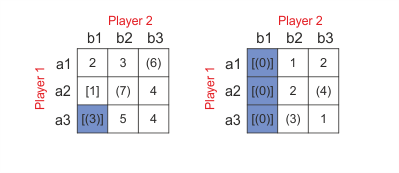
Exercise 2
references
- ↑ [DARITY, William A. International encyclopedia of the social sciences [online] http://www.columbia.edu/~rs328/NashEquilibrium.pdf. 2008. vyd. Detroit: Macmillan Reference USA, 2008, s. 540-542 [cit. 2013-01-25]. ISBN 9780080430768.]
- ↑ 2.0 2.1 2.2 2.3 [OSBORNE, Martin J. Draft chapter from An introduction to game theory [online] http://www.economics.utoronto.ca/osborne/igt/nash.pdf. Version: 2002/7/23. s. 11-52 [cit. 2013-01-25].]
- ↑ 3.0 3.1 3.2 3.3 3.4 [DLOUHÝ, Martin. Úvod do teorie her. 2., přeprac. vyd. Praha: Oeconomica, 2009, 119 s. ISBN 978-80-245-1609-7.]
- ↑ 4.0 4.1 4.2 [ROSEN, Alon a Ran CANETTI. Cryptography and Game Theory: Lecture 6: Basics of Game Theory. [online] http://www.cs.tau.ac.il/~canetti/f09-materials/f09-scribe6.pdf [cit. 2013-01-25]. ]
- ↑ [NASH, John F. Nobelprize.org: John F. Nash autobiography. [online] http://www.nobelprize.org/nobel_prizes/economics/laureates/1994/nash-autobio.html 1994 [cit. 2013-01-25].]