Poissonovo rozdělení
Contents
Úvod
Poissonovo rozdělení pravděpodobnosti patří mezi diskrétní pravděpodobnostní rozdělení. Mezi diskrétní rozdělení pravděpodobnosti také patří alternativní, rovnoměrné, binomické a hypergeometrické rozdělení. Poissonovo rozdělení udává buď počet událostí, které nastanou za daný časový úsek, nebo počet výskytů daného objektu v dané geometrické oblasti. Jevy musí nastat nezávisle na sobě a se stejnou pravděpodobností výskytu. [1]Poissonovo rozdělení se též nazývá jako tzv. zákon malých čísel, který značí výskyt jevů, jenž se vyskytují zřídka, ale mají mnoho příležitostí nastat.[2]
Jako jednoduchý příklad Poissonova rozdělení lze uvést situaci v obchodě - lze vypočítat pravděpodobnost, že prodavačka obslouží tři zákazníky za 30 minut, když víme že běžně za hodinu obslouží šest zákazníků. Takovýto typ příkladu je naprosto typický pro Poissonovo rozdělení.
Definice
Náhodná veličina X má Poissonovo rozdělení Po(Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda}
) právě tehdy, když má pravděpodobnostní funkce tvar:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(x) = \frac{\lambda^x}{x!}\mathrm{e}^{-\lambda},pro\,x_i =0,1,2,..., \; \lambda_i>0}
Případně Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(x) = \frac{l \lambda^x}{x!}\mathrm{e}^{-l \lambda}, pro\,x_i =0,1,2,..., \; \lambda_i>0}
v úseku délky l (v l-násobku délky jednotkového úseku).
Charakteristika
Poissonovo rozdělení pracuje s proměnnými v určitém čase. Má čtyři základní vlastnosti:
- proměnná Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} označuje průměrný počet vyskytlých jevů v ohraničeném úseku,
- pro každý časový okamžik je pravděpodobnost jevu v malém časovém intervalu stejná (totéž platí v prostoru),
- neexistuje případ, že by nastaly dva jevy přesně v jednom časovém okamžiku nebo místě v prostoru,
- jednotlivé jevy jsou na sobě nezávislé. [3]
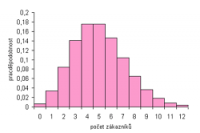
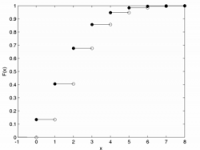
Vpravo je zobrazena pravděpodobnostní a distribuční funkce tohoto rozdělení. Na horizontální ose vyskytuje proměnná k, která značí počet výskytů daného jevu, v tomto případě počet zákazníků. Svislou osou je hodnota pravděpodobnosti průměrného výskytu daného jevu, tedy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} .
Vztah Poissonovo a binomického rozdělení
Pokud má náhodná veličina binomické rozdělení, tvar jejího rozložení se blíží k Poissonovu s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda = n \cdot p} , jestliže n je velké a p se blíží k nule. Je tedy možné aproximativně binomické rozdělení s velkým n a malou hodnotou p nahradit Poissonovým rozdělením. [3]
Vzorce
- Pravděpodobnostní funkce: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(x) = \frac{\lambda^x}{x!}\mathrm{e}^{-\lambda}, pro\,x_i =0,1,2,..., \; \lambda_i>0} [3]
- Distribuční funkce: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad \sum_{x_i \le x}i \frac{\lambda^x}{x!}\mathrm{e}^{-\lambda}} [5]
- Střední hodnota: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad \operatorname{E}(X)=\lambda} [3]
- Rozptyl: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad \operatorname{D}(X)=\lambda} [3]
- Směrodatná odchylka: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma = \sqrt{\lambda}} [3]
- Koeficient šikmosti: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad \gamma_1 = \frac{1}{\sqrt{\lambda}}} [3]
- Koeficient špičatosti: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad \gamma_2 = \frac{1}{\lambda}} [3]
Modelový příklad
Poissonovo rozdělení je užitečné především v případě, kde měříme velikost proměnné v určitém časovém intervalu. Zde jen je uvedeno několik obecných příkladů použití:
- Predikce prodeje určitého výrobku
- Počet ošetřených pacientů během dopolední špičky
- Počet uchazečů o práci v oddělení managementu
Zadání: Během jedné hodiny spojí sekretářka řediteli v průměru 6 hovorů. Potřebujeme sledovat zatížení sekretářky ve 20-ti minutových intervalech. Popište náhodnou veličinu udávající počet spojených telefonních hovorů během 20 minut pomocí pravděpodobnostní funkce. Dále s využitím distribuční nebo pravděpodobnostní funkce určete, že během 20 minut sekretářka spojí:
- Více než tři hovory
- Jeden nebo dva hovory[4]
- Nejprve určíme parametr Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda }
, tedy střední hodnotu. Jelikož víme, že za hodinu sekretářka vyřídí 6 hovorů, střední hodnota jsou 2 telefonáty. Z toho vyplývá tvar pravděpodobnostní funkce:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad P(x) = \frac{2^x}{x!}\mathrm{e}^{-2}} - Nyní spočítáme, že během 20 minut sekretářka spojí
- Více než tři hovory
K tomu, abychom zjistili tuto pravděpodobnost, nejprve spočítáme hodnotu distribuční funkce pro tři hovory. Tuto hodnotu poté odečteme od jedničky a zjistíme tu, která značí více jak tři hovory.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X>3)=1-P(X \le 3)=1-F(3)=1-{\qquad \sum_{x=0 }^3 \frac{2^x}{x!}\mathrm{e}^{-2}}=0,8571=86%} - Jeden nebo dva hovory
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X=1 \or X=2)=p(1)+p(2)=0,2707 + 0,2707 = 0,541 = 54%}
Funkce v Excelu
Poissonovo rozdělení lze také počítat v programu Excel. Tam je k tomu určená přímo funkce, která má tvar POISSON. DIST(x, střední, kumulativní) a má tyto parametry:
- X = počet výskytů, povinný údaj
- Střed_hn = střední hodnota, povinný údaj
- Kumulativní = tato hodnota rozhoduje, v kterém typu rozdělení se má vrátit daná pravděpodobnost, přičemž se rozhoduje skrz hodnota PRAVDA, která vrátí kumulativní rozdělení, či NEPRAVDA, která vrátí hromadné rozdělení pravděpodobnosti. [6]
Příklad
Zadání: Kuchařka v jídelně nandá průměrně 5 porcí za 5 minut. Zjistěte jaká je pravděpodobnost, že počet porcí za 5 minut bude větší než 4.
Náhodná veličina X - počet zákazníků přesně splňuje kritéria pro Poissonovo rozdělení. Pravděpodobnostní funkce počtu zákazníků má tedy tvar:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \qquad P(x) = \frac{5^x}{x!}\mathrm{e}^{-5}}
Úlohu nejlépe vyřešíme pomocí opačného jevu – zjistíme pravděpodobnost toho, že počet porcí za 5 minut bude menší než 4. Poté tuto hodnotu odečteme a získáme pravděpodobnost, která nás zajímá – tedy počet porcí větší než 4:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X>4)=1-P(X \le 4)=1-p(0)-p(1)-p(2)-p(3)-p(4)=1-0,44=0,56}
Nyní toto vyjádříme v excelu pomocí funkce POISSON.DIST. Počet výskytů jsou čtyři, jelikož zjišťujeme pravděpodobnost tohoto údaje. Jako střední hodnotu dosadíme číslo pět, jelikož je to průměrná hodnota. A jelikož se ptáme na pravděpodobnost za daný časový úsek, tak poslední hodnota je PRAVDA – ptáme se na distribuční funkci. Do excelu zadáme tento vzorec:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle POISSON.DIST(4;5;PRAVDA)=0,44}
Tuto hodnotu odečteme od 1 a dostaneme kýženou pravděpodobnost – 1 - 0,44 = 0,56.
Fakta související s problémem
Poissonovo rozdělení pracuje s výskytem jevů za daný časový interval, jak již bylo zmíněno výše. S tím souvisí dva důležité koncepty – teorie hromadné obsluhy a teorie obnovy.
Teorie hromadné obsluhy
S Poissonovým rozdělením úzce souvisí i teorie hromadné obsluhy - obojí je úzce spojeno s pravděpodobností a časovou jednotkou. Jde o model, když požadavky prochází zařízeními, od kterých očekávají obsluhu. Vlivem omezené kapacity poté může docházet k frontám, proto se této teorii také alternativně říká ,,teorie front“. [7]
V souvislosti s Poissonovým rozdělením je potřeba vysvětlit dva pojmy – intenzitu příchodů a intenzitu obsluhy. Intenzita příchodů (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda}
) je průměrná hodnota příchodu určitých jednotek – např. průměrně přichází do obchodu 5 zákazníků za minutu - Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda=5 \text{ zákazníků za minutu}}
. Jakmile je jednotka v systému, lze vypočítat průměrnou hodnotu, za jakou bude jednotka obsloužena – tomu se říká intenzita obsluhy(µ). Jako příklad lze uvést opět situaci v obchodě – prodavačka obslouží průměrně 100 zákazníků za hodinu -Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu =100 \text{ zákazníků za hodinu}}
.[7]
Příchod vstupů může být buď pravidelný nebo nepravidelný. Pokud například v obchodě vstupují zákazníky nepravidelně, zde už teorie front souvisí s pravděpodobností – a to buď s Poissonovým rozdělením nebo exponenciálním. Pokud bychom chtěli znát například počet zákazníků vstupujících do supermarketu za určitý časový interval, použijeme právě Poissonovo rozdělení. Pokud bychom naopak chtěli vypočítat dobu, za kterou přijde jeden zákazník za druhým, tak bychom museli zvolit exponenciální rozdělení. [8]
Teorie obnovy
Teorie obnovy zkoumá závislosti prvků, které selhávají a v závislosti na to jsou nahrazovány novými prvky. Je nejen zobecněním Poissonova procesu, ale také je přímo napojena na teorii spolehlivosti. To, kdy prvky selžou, je náhodná veličina, a pomocí Poissonova rozdělení zde vypočítat pravděpodobnost selhání v určitém časovém úseku. Jednoduchý příklad takového prvku je žárovka – v jejím případě je selháním to, že praskne. [9] Proces obnovy lze dělit na dva typy – proces s okamžitou obnovou a proces s konečnou dobou obnovy. Proces s okamžitou dobou obnovy je ta situace, když je doba obnovy daného prvku zanedbatelná vůči době bezporuchovosti. Jako příklad lze uvést opět onu žárovku. Když máme dáno, že dokáže svítit 1000 hodin a vyměňujeme žárovku pouze 30 minut, je to hodnota velmi malá a zanedbatelná. Proces může být ale i s konečnou dobou obnovy, kde se také vyskytuje Poissonovo rozdělení, jelikož pracuje s náhodnou veličinou. Doba bezporuchovosti je stejně náhodná jako doba veličiny. Teorie obnovy je velmi náročná část matematiky a vyžadovala by vlastní samostatnou kapitolu, je tu tudíž zmíněna pouze teoreticky. [9]
Příklady k procvičení
Řešení k níže uvedeným příkladům je v tomto souboru.
- Při provozu balícího automatu dochází během dne k náhodným poruchám.Ze zkušenosti víme, že během jedné směny dojde v průměru ke dvou poruchám. Jaká je pravděpodobnost, že během 24 hodin (třísměnný provoz) nedojde k žádné poruše? [1]
- K automatu přijde v průměru 30 zákazníků za 1/2 hodiny. Jaká je pravděpodobnost, že během příštích pěti minut přijde k automatu právě jeden zákazník? Vypočítejte také střední hodnotu, rozptyl a směrodatnou odchylku.[1]
Reference
- ↑ 1.0 1.1 1.2 NEUBAUER, Jiří, Marek SEDLAČÍK a Oldřich KŘÍŽ. Základy statistiky: Aplikace v technických a ekonomických oborech. 2. rozšířené vydání. Praha: Grada Publishing, 2016. ISBN 978-80-247-5786-5
- ↑ CHARPENTIER, Arthur. The law of small numbers . Freakonometrics, 2013 [online]. [cit. 2021-04-21]. Dostupné z: https://freakonometrics.hypotheses.org/1416
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 OTIPKA, Petr a Vladislav ŠMAJSTRLA. Pravděpodobnost a statistika. Ostrava: Vysoká škola báňská - Technická univerzita Ostrava, 2006. [online]. [cit. 2021-04-23]. Dostupné z: https://homel.vsb.cz/~oti73/cdpast1/
- ↑ 4.0 4.1 NEUBAUER,Jiří. Modely diskrétní náhodné veličiny . Katedra ekonometrie, FVL, UO Brno, nedatováno [cit. 2021-4-29]. Dostupné z: https://k101.unob.cz/~neubauer/pdf/diskretni_modely.pdf
- ↑ BUDÍKOVÁ, RNDr. Marie. Poissonovo rozdělení. Brno: Přírodovědecká fakulta Masarykovy univerzity, 2016 [online]. [cit. 2021-04-29]. Dostupné z: https://is.muni.cz/do/rect/el/estud/prif/ps15/statistika/web/pages/poissonovo-rozd.html
- ↑ Microsoft Support POISSON.DIST (funkce). Microsoft, 2019 [online]. [cit. 2021-04-21]. Dostupné z: https://support.microsoft.com/cs-cz/office/poisson-dist-funkce-8fe148ff-39a2-46cb-abf3-7772695d9636
- ↑ 7.0 7.1 SEKNIČKOVÁ, Jana. Modely hromadné obsluhy [přednáška]. Praha: VŠE Fakulta informatiky a statistiky, 2020. Dostupné z: http://jana.kalcev.cz/vyuka/kestazeni/4EK212-KVAM/KVAM-dist/S11%20-%204EK212%20KVAM%20-%20web.pdf
- ↑ ŽIŽKA,Miroslav.Teorie front.Nedatováno [online]. [cit. 2021-04-25]. Dostupné z: http://multiedu.tul.cz/~miroslav.zizka/multiedu/Teorie_front_1.pdf
- ↑ 9.0 9.1 RIS, Radim. Systémy údržby. Ostrava: Vysoká škola báňská - Technická univerzita Ostrava, 2007 [online]. [cit. 2021-04-30]. Dostupné z: http://www.elearn.vsb.cz/archivcd/FS/TU/TU/