Bank branch checkout optimalization
Contents
Information
• Project name: Bank branch checkout optimalization
• Class: 4IT496 (WS 2016/2017)
• Author: Bc. Josef Zeman
• Model type: Discrete-event simulation
• Software used: SimProcess, trial version
Problem definition
This simulation is going to be focused on optimalization of open check-outs (counters) at the bank branch. Given the fact these simulations should be relatable to the real world, I chose branch of Česká spořitelná on the street Na příkopech, where I got the numbers from the call-out system. This system distributes visitors accordingly to the capacity of the branch as well as to selected issue visitiors want to solve (there are only 2 services – cash services and account services). These data should vary during week. Every counter can serve just one of the issue mentioned above.
Goal of the simulation: Main point is to ideally and optimally assign human resources to counters accordingly given the daytime and the period of week.
I was given data from 28.11.2016 through to 2.12.2016 and I believe that these information are valid through all year.
Aggregated real data
The number of customers was most often very similar therefore I decided to ease myself the work and unified it through the days. Mondays and Fridays were very similar to each other so I combined them together as well as the other 3 work days that were combined together as well. Following lines should give the basic idea what was the distribution like.
First service
Monday/Friday
9:00:00 - 10:30:00 40 per hour
10:30:00 - 12:00:00 25 per hour
12:00:00 - 13:30:00 35 per hour
13:30:00 - 16:30:00 28 per hour
16:30:00 - 18:15:00 35 per hour
18:15:00 - 19:00:00 15 per hour
Thursday/Wednesday/Thursday
9:00:00 - 10:30:00 35 per hour
10:30:00 - 12:00:00 20 per hour
12:00:00 - 13:30:00 31 per hour
13:30:00 - 16:30:00 25 per hour
16:30:00 - 18:15:00 32 per hour
18:15:00 - 19:00:00 12 per hour
Second service
Monday/Friday
9:00:00 - 10:30:00 11 per hour
10:30:00 - 12:00:00 8 per hour
12:00:00 - 13:30:00 11 per hour
13:30:00 - 16:30:00 9 per hour
16:30:00 - 18:15:00 12 per hour
18:15:00 - 19:00:00 5 per hour
Thursday/Wednesday/Thursday
9:00:00 - 10:30:00 10 per hour
10:30:00 - 12:00:00 7 per hour
12:00:00 - 13:30:00 10 per hour
13:30:00 - 16:30:00 7 per hour
16:30:00 - 18:15:00 10 per hour
18:15:00 - 19:00:00 5 per hour
Model
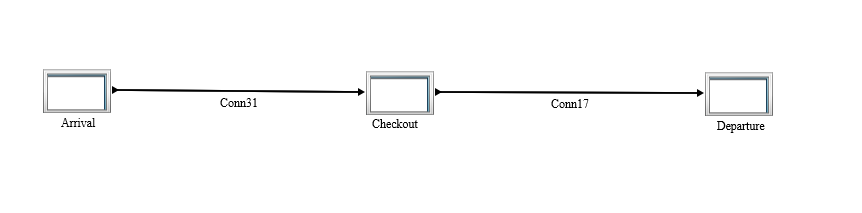
The model itself is really easy since there are no extra activities involved. Therefore there are just 3 main processes like in the picture below:
Arrival – generator of customers for each service
Checkout – delay activity that represents the checkout
Departure – dispose activity of served customers
This covers 2 kinds of service:
Service 1 – cash services (average time spent on the checkout are 4 minutes)
Service 2 – account services (average time – 10 minutes)
Entities
There are only 2 entities in this model – customers of 1st (cash service) and 2nd service (account service)
Resources There are 4 resources in total – 2 different checkout counters and 2 different kinds of clerks. For the first service there are 4 counters and 4 cashiers at max and for the second service it is 3 counters and 3 cashiers at max.
Processes
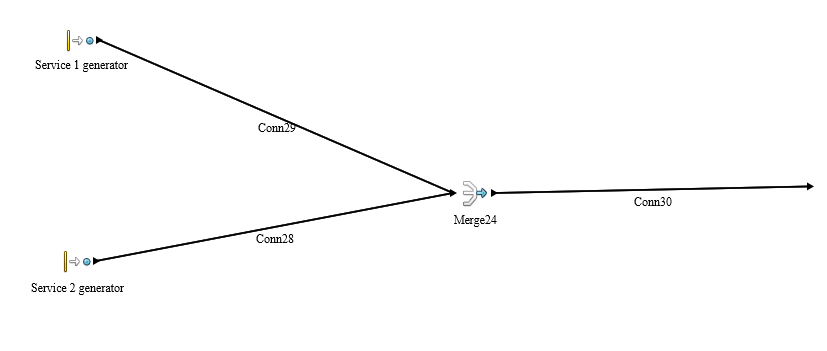
Arrival
Simple process with 2 generator activities for each service, these 2 merge together for the downstreaming the meaning and similarity of process.
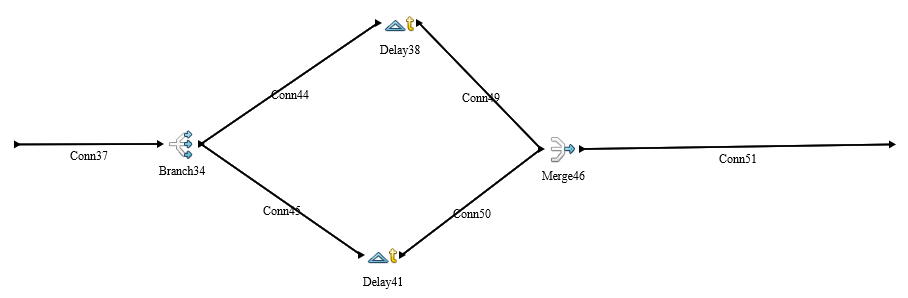
Checkout
Branch activity divides the customers according to the Entity type and distributes them to correct checkout counter. Customers for each counter willing to wait for different amount of time. For first service it is 10 minutes and for the second service it is 20 minutes.
Departure
Simple process where the served customers are disposed.
Optimal model
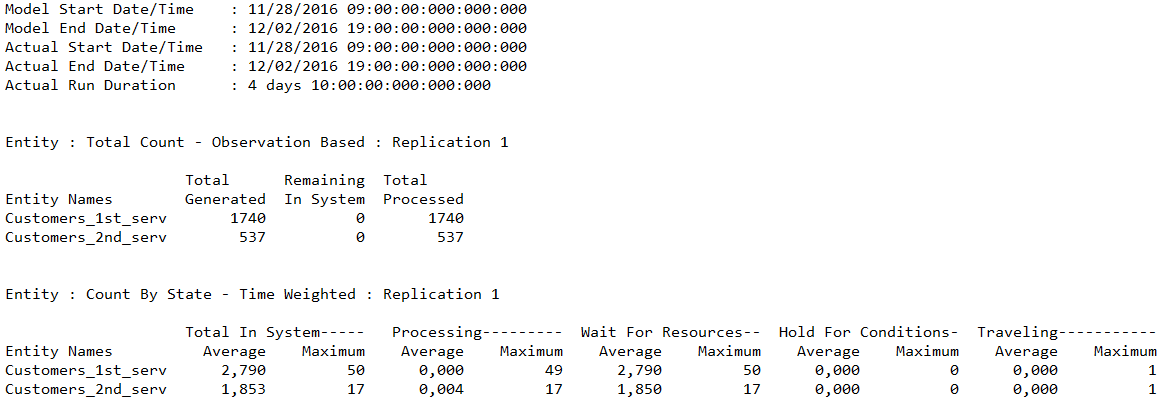
From the first look at the presented data from the call-out system it is very well visible that the branch has much larger capacity than is needed. From simple calculations I got to optimal number of open counters quite easily within each day. From the downtime is visible that all checkouts have never been opened, since it wasnt necessary. During most of the day very n-1 checkouts open and the number lovered within the last hour of open to n-2.
As it is visible from the results, the average wait time was just a fraction of the time before the would start to leave so this milestone was met.