Kooperativní hry
Kooperativní hra, spadající do oblasti teorie her označuje takovou hru, ve které mají hráči možnost vzájemné kooperace, tedy spolupráce. Toto rozšíření, respektive možnost jim umožnňuje volit svoji strategii na základně ostatních. Tím je myšleno, před volbou své strategie vyjednat a uzavřít úmluvu s jinými hráči, jakou strategii zahrají oni. Cílem tvorby těchto úmluv (dohod) je zvýšení zisku, nebo výhry kombinací strategií v dané hře. Při uzavření úmluvy je povinností hráče dodržet dané podmínky. Avšak koncept spolupráce není povinný. Ke spolupráci dojde pouze, když souhlasí obě strany. A podmínka souhlasu je většinou jasná, pokud spolupráce přinese hráči větší užitek (výhodu), než když by hrál sám. Jinak řečeno, kooperací získám víc, než kdybych hrál na vlastní triko.
Základní příklad: Hráči Alice a Bob hrají hru, kde rozvíjejí své město. Alicino okolí tvoří z 90 procent lesy a z 10 procent železnými doly. Naopak okolí Bobova města tvoří z 90 procent železné doly a z 10 procent lesy. Alice má dostatek dřeva na stavbu nových domů, ale nedostatek železa pro tvorbu oceli na zbraně. Bob je na tom opačně, disponuje železem na výrobu zbraní, ale má nedostatek dřeva. Hra poskytuje směnu surovin, ovšem s příplatkem zlata a v nevýhodném kurzu. Alice a Bob se mohou domluvit (kooperovat), že každý nebude draze měnit suroviny s hrou, ale vymění je navzájem. Vytvoří úmluvu (dohodu), ve které si specifikují směnný poměr surovin a dle tohoto poměru si vzájemně vymění suroviny, aby dosáhli vyššího zisku. Navíc ušetří zlato, které bylo jako poplatek za směnu.
| Před čtením tohoto učebního textu je ideální seznámit se s tématy teorie her, Nashovy rovnováhy případně jednorázové hry. |
Contents
Kooperativní hry dvou hráčů
Kooperativní hry dvou hráčů jsou zvláštní tím, že pokud dojde ke vzájemné spolupráci, kooperují všichni (oba) hráči. Narozdíl od kooperace více hráčů, kde se všichni hráči nemusí zapojit a některý může hrát bez využití spolupráce. U totoho druhu hry platí taktéž pravidlo, že spolupráce mezi dvěma hráči se uskuteční pouze, pokud to přinese oběma hráči stejný vyšší zisk (výhru), než kdyby nespolupracovali. Pokud jeden z hráčů nezíská na kooperaci více, než při nekooperativní hře, nemá důvod tvořit dohodu s druhým hráčem.
Teorie
Posléze maximální celkovou částka, kterou mohou hráči získat dohromady kooperací je vyjádřena následujícím vztahem:
kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f_1} vyjadřuje výplatní funkci prvního hráče, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f_2} výplatní funkci druhého hráče, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} vyjadřuje zvolenou strategii prvního hráče a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} zvolenou strategii druhého hráče.
Pokud platí podmínka Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) > v(1) + v(2)} , čili celková částka (výhra) získaná kooperací je větší, než součet rovnovážných zaručených výher obou hráčů, tak je pro hráče výhodné utvořit dohodu a ve hře kooperovat. Posléze tedy optimální strategie, kterou by měli hráči zahrát, odpovídá hodnotě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2)} . Tuto hodnotu nalezneme tak, že provedeme součet výplatních matich jednotlivých hráčů a najdeme maximální hodnotu v této nové matici.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = v(1,2)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 \geq v(1)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)}
Slovním popisem:
- výhra kooperací hráče 1 sečteno s výhrou kooperací hráče 2 se musí rovnat maximální celkové částce kooperace
- výhra kooperací hráče 1 musí být větší nebo rovna rovnovážné zaručené výhře hráče 1
- výhra kooperací hráče 2 musí být větší nebo rovna rovnovážné zaručené výhře hráče 2
Tuto množinu rozdělení parametrů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2} , splňující předchozí podmínky, nazýváme jádro hry.
Jádro hry
Jádro hry je tedy množinou kombinací výher jednotlivých hráčů při kooperativní hře. Není však přesně popsáno, jak rozdělit celkový zisk, respektive kolik si který hráč vezme z celkové výhry.[1]
- Každý hráč dostane polovinu celkové výhry kooperací, pokud takovéto rozdělení splňuje podmínky jádra hry.
- Každý hráč dostane zaručenou výhru a polovinu z části, co hráči získali kooperací navíc.
- Rozdělení celkové výhry v poměru, například dle rovnovážných zaručených výher, či předem dohodnutém poměru.
Vzorce pro typy výher jsou následující:
- Každý hráč dostane polovinu celkové výhry kooperací:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = a_2 = \frac{v(1,2)}{2}}
- Každý hráč dostane zaručenou výhru a polovinu ze zbytku po kooperaci:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1* = v(1) + \frac{[v(1,2) - v(1) - v(2)]}{2}}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2* = v(2) + \frac{[v(1,2) - v(1) - v(2)]}{2}}
- Rozdělení výhry v poměru ke společné výhře:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 : a_2 = [v(1,2) - v(2)] : [v(1,2) - v(1)]}
Kooperativní hry s přenosnou výhrou
Jedná se o situaci, kdy je výhra přenosná, tudíž hráči mohou určitým způsobem celkovou výhru kooperace přerozdělit mezi sebe. Byť při této hře může dojít k situaci, že by jeden hráč při kooperaci dostal menší výhru, než svou zaručenou při nekooperaci, tak tím, že je výhra přenosná, sdílení a rozdělení výhry dostane chvilkově znevýhodněného hráče do lepší pozice, než při nekooperaci. [2]
Kooperativní hry s nepřenosnou výhrou
Jedná se o situaci, pokud je výhra nepřenosná, každý hráč získá výhru ze své výplatní matice a nedostane podíl z celkové části. To znamená, že nedochází k možnostem dělení celkového zisku mezi hráče, ale výhra je vyplacena v poměru, který udává výplatní matice dané kombinaci strategií. Nepřenosná výhra se tedy může stát pro jednoho hráče extrémně výhodnou, naopak pro druhého hráče extrémně nevýhodnou. Posléze se tedy stává, že druhý hráč do kooperace nevstoupí, respektive nemá zájem, jelikož jeho zaručená výhra je větší, než výhra při kooperativní hře s nepřenosnou výhrou. Ovšem mohou nastat situace, kdy kooperace bude výhodná pro oba hráče, poté by mělo ke kooperaci dojít. [2]
Příklady
V následující části jsou dva příklady, jeden na bližší porozumnění přenosné a nepřenosné výhry. Druhý, konkrétní příklad kooperativní hry pro dva hráče s rozdělením celkové výhry.
Příklad kooperativní hry s přenosnou a nepřenosnou výhrou
Vezměme příklad, kdy je zadána hra pro dva hráče s následující výplatní maticí pro dva hráče:
| X | Y | |
|---|---|---|
| A | 3,5 | 11,3 |
| B | 5,6 | 7,4 |
Jelikož jde o kooperační hru, sečteme hodnoty v daných buňkách (sečteme výplatní matice každého hráče) a vyjde nám celková výhra dané kombinace strategií, která se rovná maximální hodnotě tabulky. Součet výplatních matic ukazuje tabulka č.2:
| X | Y | |
|---|---|---|
| A | 8 | 14 |
| B | 11 | 11 |
Nyní určíme základní parametry. Rovnovážným řešením při nekooperaci je strategie (B,X), které mají výhry (5,6). Z toho určíme, že zaručená výhra hráče 1 je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1) = 5} a zaručená výhra hráče 2 je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(2) = 6} . Rovnovážným řešením při kooperaci je strategie (A,Y) s celkovou výhrou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) = 11 + 3 = 14} .
Přenosná výhra: Hráči mohou sdílet výhru! Byť hráč 2 má zaručenou výhru při nekooperaci Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(2) = 6} a při kooperaci dostane v základu výhru 3 (dle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) = (11,3)} ), tak se mu stále vyplatí spolupracovat, jelikož hráč 1 se s ním o svou výhru 11 podělí. Ve finále, pokud by si dělili celkovou výhru kooperace na půl, tak by každý z hráčů obdržel výhru 7. Z toho vyplývá Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = a_2 = 7} .
Současně jsou splněny podmínky výher:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7 + 7 = 14} - podmínka součtu výher se rovná celkové výhře kooperace
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7 \geq 5} - podmínka hráče 1, výhra při kooperaci je větší než rovnovážná zaručená výhra při nekooperaci
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7 \geq 6} - podmínka hráče 2, výhra při kooperaci je větší než rovnovážná zaručená výhra při nekooperaci
Nepřenosná výhra: Hráči nemohou sdílet výhru! Rovnovážná zaručená výhra hráče 2 při nekooperaci je 6. Při kooperaci by v tuto chvíli obdržel hráč 1 výhru 11 a hráč 2 výhru 3. Tyto výhry se stanou finálními, nedojde k žádnému sdílení. Kooperace se tudíž stává pro hráče 2 nevýhodná a hráč 2 spolupracovat nebude, protože nekooperace mu přinese větší výhru, než kooperace.
Z toho důvodu není splněna podmínka Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3 \geq 6} - výhra při kooperaci je větší než rovnovážná zaručená výhra při nekooperaci.
Příklad kooperativní hry pro dva hráče
| 3 | -3 |
| 4 | 1 |
| 5 | -1 |
| 1 | 4 |
| 8 | -4 |
| 5 | 5 |
Pokud bychom spojili matici A a B dohromady a chtěli určit Nashovu rovnovážnou strategii, byla by to strategie(2,2), v pravé dolní buňce, se zaručenými výhrami (1,4). Z toho tedy vyplývá, že rovnovážná zaručená výhra hráče 1 je 1 a rovnovážná zaručená výhra hráče 2 je 4.
Pro vyhledání ideální strategie kooperace hledáme v tabulce č.5 největší hodnotu. Tu nalezneme v levé horní buňce, strategie (1,1) a její hodnota je 8. Tato hodnota je taktéž maximální celková výhra kooperace.
Doposud známé parametry:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1) = 1}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(2) = 4 }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) = 8 }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = 8 }
Při kooperační hře s nepřenosnou výhrou by se Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = 3} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 = 5 } a všechny podmínky by byly splněny:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) > v(1) + v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8 > 1 + 4}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = v(1,2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3 + 5 = 8}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 \geq v(1)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3 \geq 1}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5 \geq 4}
Při kooperační hře s přenosnou výhrou spočítáme možnosti výhry dle možností dělení celkové výhry:
- Každý hráč dostane polovinu celkové výhry kooperací:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = a_2 = \frac{8}{2} = 4}
- Každý hráč dostane zaručenou výhru a polovinu ze zbytku po kooperaci:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1* = 1 + \frac{[8 - 1 - 4]}{2} = 2,5}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2* = 4 + \frac{[8 - 1 - 4]}{2} = 5,5}
- Rozdělení výhry v poměru ke společné výhře:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 : a_2 = [8 - 4] : [8 - 1] = 4 : 7}
Ve výsledku všechny kombinace rozdělení výher splňují podmínky, proto se vyplatí oběma hráčům kombinovat.
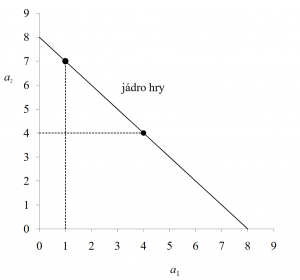
Jádro hry v grafu
Na grafu lze vidět vyobrazení jádra hry. V tomto případě má jádro podobu úsečky mezi vyznačenými body. Přerušované čáry vyznačují právě tyto body a jsou to minima výhry pro daného hráče. Tím je myšleno, hráč 2 musí mít výhru větší jak 4, aby se mu kooperace vyplatila. To samé platí pro hráče 1, akorát u něj je minimální výhra 1. Pokud bychom se tedy pohybovali po přímce, nalezneme mnoho možností, jak rozdělit výhru mezi hráče. Například 2, 6 nebo 3, 5 a podobně (samozřejmě lze zajít i do desetinných míst). Nesmíme se však dostat u hráče 1 pod hodnotu 1 a u hráče 2 pod hodnotu 4.
Zajímavost
U tohoto druhu hry je možný alternativní způsob stanovení zaručené výhry. Jedná se totiž o stav, kdy by protihráč (hráč 2) volil pro hráče 1 nejhorší možnou strategii. Čili hráč jedna by hrál svou optimální strategii a hráč 2 nejhorší možnou strategii pro hráče 1. Pro odlišení výše definované zaručené výhry se tato nazývá maximinová zaručená výhra. Tato výhra se určí tak, že v prvním kroku určíme pro hráče 1 řádková minima a pro hráče 2 sloupcová minima. Z těchto nazelených minim následně vybereme maximální hodnoty.[1]
Pokud bychom tuto metodu aplikovali na příklad rozebraný výše, tak pro prvního hráče jsou řádková minima -3 a 1, pro druhého hráče jsou sloupcová minima 1 a -1. Dle pravidel tedy z těchto minim vybereme maximální hodnotu a ve výsledku lze konstatovat, že maximonová zaručená výhra má pro oba hráče hodnotu 1.
Tento postup se používá u dvoumaticových her s více než jedním Nashovým rovnovážným řešením, protože u těchto her je obtížné určit rovnovážnou zaručenou výhru.
Kooperativní hry více hráčů
V předchozím části jsme se zabývali pouze možností, že máme dva hráče a ti spolu buď kooperují, nebo jdou proti sobě, nekooperují. U her s více hráčů, kde rozumějmě nastává situace počtu hráčů > 2, nastává situace, kdy někteří hráči spolu mohou kooperovat, někteří nemusí. Otázkou ale zůstává, s kým spolupracovat a proti komu. Skupinu hráčů, kteří spolupracují při volbě strategií nazýváme koalicí, z toho odvozeno koaliční hry.
Koaliční hry
Definice
„Nechť N = {1, 2, 3, ..., N) je množina hráčů, potom koalicí hráčů rozumíme každou podmnožinu S množiny hráčů N. V případě, že S se shoduje s N, jsou v koalici všichni hráči a hovoříme o velké koalici.“[3] |
Není radno opomenout, že pokud hráč nevstoupí do žádné koalice, sám tvoří jednoprvkovou koalici. To znamená, že velká koalice existuje jen tehdy, jsou-li všichni hráči v jedné koalici. Hra více hráčů taktéž otevírá nové možnosti kombinací kooperací. S růstem počtu hráčů roste množství kombinací koalic, které lze vytvořit. Ve hře s N hráči lze vytvořit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2^N - 1} koalic a jeden hráč může být členem v Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2^{N-1} - 1} různých koalic. Pro ukázku, v koaliční hře s třemi hráči se naskýtá již pět možných řešení koalic:
- Všichni hráči hrají samostatně (každý tvoří jednoprvkovou koalici).
- Všichni hráči spolupracují (tvoří velkou koalici).
- První a druhý hráč spolupracují proti třetímu, který tvoří jednoprvkovou koalici.
- První a třetí hráč spolupracují proti druhému, který tvoří jednoprvkovou koalici.
- Druhý a třetí hráč spolupracují proti prvnímu, který tvoří jednoprvkovou koalici.
Množina všech utvořených koalic v rámci jedné hry se nazývá koaliční struktura. Ve hře sedmi hráčů je koaliční struktura definována například takto: ({1, 3, 5},{4, 2},{6},{7}). Ve hře tedy vznikly čtyři koalice. V první koalici spolupracují hráči 1, 3 a 5, ve druhé hráči 4 a 2 a na konec existují dvě jednoprvkové koalice, jedna obsahuje hráče 6 a druhá hráče 7. Tito hráči s nikým nespolupracují. Pro typické konfliktní situace je předpokladem hra s volnou disjunktivní koaliční strukturou. Tato koaliční struktura udává, že jsou přípustné jakékoli koalice a hráč může být členem pouze jedné koalice. Počet možných koaličních struktur při volné disjunktivní koaliční struktuře lze vypočítat podle následujícího vzorce:[3]
Ve výsledku dostáváme počet všech možných koaličních struktur při daném počtu hráčů. Pro ukázku, zde je pár hodnot: R(2)=2, R(3)=5, R(4)=52 a počet možných koalicí se s počtem hráčů rapidně zvyšuje.
Charakteristická funkce
„Charakteristickou funkcí hry s množinou hráčů N nazveme takovou funkci v, která je definována pro všechny podmnožiny S, to jest pro všechny koalice, kterých je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2^N - 1} . Každé koalici charakteristická funkce přiřazuje hodnotu v(S), což je výhra koalice S.“[3] |
Charakteristickou funkci lze přirovnat k výplatní funkci, která se objevuje například u výše zmíněných kooperací dvou hráčů. Rozdílem je, že charakteristická funkce určuje výpaty koalicím, nikoliv hráčům. Hodnotu charakteristické funkce pro koalici S lze určit na základě dvou předpokladů:
- Hráči mimo koalici S volí své rovnovážné strategie. Poté říkáme, že se jedná o rovnovážnou charakteristickou funkci.
- Hráči mimo koalici S volí své nejhorší možné strategie z pohledu koalice S, aby ji záměrně poškodily. Poté říkáme, že se jedná o maximinovou charakteristickou funkci.
Pokud jsou hráči smysluplní, tak zvolí rozhodně rovnovážnou charakteristickou funkci, jelikož hráči mimo koalici S by měli chtít také maximalizovat svou výhru, než trestat koalici S a zároveň sebe.
Superaditivita
Říkáme, že charakteristická funkce je superaditivní, pokud pro každou dvojici koalic platí:[3]
kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_1, S_2 } jsou disjunktivní podmnožiny množiny N. Slovně řečeno, v případě vytvoření vyšší (větší) koalice je výhra větší nebo rovna součtu výher menších koalic. Ovšem v praktických příkladech ne vždy toto pravidlo platí. Například při hře tří hráčů může být pro dva spolupracující hráče výhodnější spolupracovat pouze ve dvou a nechat třetího v jednoprvkové koalici, než vytvořit koalici tří hráčů.
Rozdělení výhry
Předpoklady rozdělení výher jsou následující:[3]
- Jde o přenosnou výhru! To znamená, že celkový zisk koalice lze rozdělit mezi její členy.
- Neexistují žádné překážky pro uzavření dohody o jakémkoliv přerozdělení výhry koalice.
- Pro jednodušší představu výhry ve hře si ji představme jako finanční částku.
- Výhra hráče se odvíjí od celkové výhry koalice jejímž je členem a od přerozdělení výhry uvnitř koalice.
Princip kolektivní racionality
Princip kolektivní racionality je zájem hráčů na maximalizaci výhry koalice. Dle tohoto principu bychom měli:[3]
- V prvním kroku sestavit koalici s nejvyšší celkovou výhrou. Pokud by takto nově vytvořená koalice obsahovala všechny hráče, postup končí a je vytvořena koaliční struktura.
- V druhém kroku sestavit opět koalici s nejvyšší výhrou, avšak za využití hráčů, kteří netvoří koalici z prvního kroku.
- Takto se pokračuje do té doby, než je ustavena úplná koaliční struktura hry!
Princip skupinové stability
Princip skupinové stability je zájem na maximalizaci výhry hráče či podskupiny hráčů při přerozdělení výhry v rámci koalice. Pro tento princip platí:[3]
- Celá výhra koalice je rozdělena mezi hráče, kteří v ní jsou.
- Každá podkoalice L musí mít při dělení výhry koalice K zajištěn minimálně takový podíl, který by si podkoalice L mohla zajistit vystoupením z koalice K.
Pro zajištění skupinové stability musí pro každou koalici K platit:
Pokud nastane situace, že některá z koalic není skupinově stabilní, je nutné se vrátit do bodu principu kolektivní racionality a utvořit novou koaliční strukturu. Tam místo nevyhovující koalice s nejvyšší výhrou zvolíme koalici s druhou nejvyšší výhrou a celý postup zopakujeme.
Jádro hry
Jádrem hry nazýváme množinu všech přípustných rozdělení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a_1, a_2, a_3, ..., a_n)} , které splňují podmínky skupinové stability. Pokud by došlo k situaci, že koaliční struktura není jednoznačně definována (charakteristická funkce by nabývala stejných hodnot pro více koalicí) a jádra daná těmito koaličními strukturami splňovala podmínky skupinové stability, měla by hra více jader. Pokud by podmínky skupinové stability nesplňovalo ani jedno rozdělení, je jádro prázdné.[3]
Shapleyův vektor - Shapleyova hodnota
Americký matematik a ekonom, Lloyd Stowell Shapley navrhl v roce 1953 Shapleyův vektor. Tato metoda slouží k odhadu síly hráče z pohledu mezního přínosu hráe ke všem koalicím, ve kterých může být členem. Následně jako Shapleyovy heodnoty se označují jednotlivé složky Shapleyova vektoru. N- rozměrný Shapleyův vektor je pro hru definován jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h = (h_1, h_2, ..., h_N)} a každá hodnota vektoru označuje střední hodnotu přínosu i-tého hráče ke všem koalicím, ve kterých může být členem. Přínos hráče ke koalici S vypočteme podle vzorce:[3]
V praktickém zápisu to může vypadat následovně: v(2, 3, 4) - v(3, 4). A tento vzorec představuje přínos hráče 2 pro koalici, do níž patří, tedy (2, 3, 4). Shapleyovu hodnotu pro i-tého hráče vypočítáme dle následujícího vzorce (vážený součet mezních přínosů daného hráče):
kde symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left|S\right|} značí počet členů koalice S a sumace probíhá pro všechny koalice, pro které platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i \in S} .
Příklad výpočtu Shapleyovy hodnoty
Počítání Shapleyovi hodnoty přes výše zmíněný vzorec by bylo matoucí, proto si ukážeme aplikaci vzorce ukážeme na lépe zapamatovatelné technice.
Existuje koaliční hra, kde N = 3, tudíž hra tří hráčů. Charakteristické funkce hry jsou zadány následovně:[3]
v({1}) = 1; v({2}) = 2; v({3}) = 3;
v({1,2}) = 2; v({1,3}) = 3; v({2,3}) = 6;
v({1,2,3}) = 6
Při výpočtu Shapleyovy hodnoty předpokládáme, že hráči přichází na místo, kde uzavírají koaliční dohody, postupně. To znamená jeden po druhém. Máme-li zadánu hru s třemi hráči, je celkem šest možností, jak mohou za sebou přijít. Tyto možnosti jsou zasenené v tabulce. Například zápis 1-2-3 značí, že nejprve přijde první hráč, posléze přijde druhý hráč, který vytvoří s prvním koalici (1,2) a následně přijde třetí a spolu vytvoří koalici (1,2,3). Teď ale přijde na řadu ohodnocení právě přínosů hráčů pro dané koalice. Přínos i-tého hráče pro danou koalici označuje logicky průsečík dané koalice a daného hráče.
Vezměme si první možnost příchodů a to 1-2-3. Jako první tedy přijde hráč 1, který má sám o sobě přínos v({1}) = 1, čili do průsečíku řádku 1-2-3 a sloupce hráč 1 píšeme hodnotu 1. Následně přichází hráč číslo 2 a uzavírá koalici s hráčem 1. Přínos druhého hráče vypočítáme tím, že vezmeme přínos koalice 1-2 a odečteme od něj přínos hráče 1, čili v({1,2}) - v({1}), čili 2 - 1, takže píšeme přínos hráče 2 hodnotu 1. Jako poslední přichází hráč 3, společně vytvoří koalici 1-2-3. Přínos třetího hráče vypočteme analogicky v({1,2,3}) - v({1,2}) čili 6 - 2, takže přínos hráče 3 ke koalici 1-2-3 je 4. A takto uděláme i ostatní řádky. Je nutné dbát na pořadí příchodů.
Pro zopakování ještě jeden řádek, tentokrát pro koalici 2-1-3. Jako první přichází hráč 2 a jeho přínos je 2. Po něm přichází hráč 1 a tvoří koalici (1,2), čili přínos koalice (1,2) 2 mínus přínos hráče 2, který je 2 dává přínos hráče 1 nula. Jako třetí přichází hráč číslo 3. Společně tvoří koalici 1-2-3, která má přínos 6 mínus přínos koalice (1,2) nám dá přínos hráče 3 roven 4.
Následně již jenom zprůměrujeme hodnoty pro dané koalice a zjistíme, který hráč má ve hře největší přínos. V tabulce jsou vypsány oba způsoby zápisu, zlomek a desetinné číslo, což je výsledek dělení zlomku.
| Postup tvorby koalice | Hráč 1 | Hráč 2 | Hráč 3 |
|---|---|---|---|
| 1-2-3 | 1 | 1 | 4 |
| 1-3-2 | 1 | 3 | 2 |
| 2-1-3 | 0 | 2 | 4 |
| 2-3-1 | 0 | 2 | 4 |
| 3-1-2 | 0 | 3 | 3 |
| 3-2-1 | 0 | 3 | 3 |
| Shapleyova hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i} | 2/6 (0,333) | 14/6 (2,333) | 20/6 (3,333) |
Po prozkoumání Shapleyových hodnot můžeme konstatovat, že nejsilnějším hráčem v naší hře je hráč číslo 3. Jeho Shapleyova hodnota je nejvyšší. Naopak nejslabší pozici při vyjednávání zastává hráč jedna, který nepřináší skoro žádný přínos, lze tedy usoudit, že by v tomto případě tvořil jednoprvkovou koalici. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i = (2/6, 14/6, 20/6)} .
Hlasovací hry
Definice
„Nechť N = {1, 2, 3, ..., N) je množina politických stran v parlamentu. Počet poslanců i-té strany bude označován jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} a celkový počet zástupců v parlamentu lze vyjádřit ve tvaru: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_0 = \sum_{i=1}^N a_i} “[3] |
kde symbol int vyjadřuje celou část součinu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha a_0} . Například: v českém politickém systému je potřeba nadpoloviční většina, aby prošel návrh zákona. Ve sněmovně je 200 poslanců. Aby hlasování prošlo, je tedy třeba Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle int(0,5 * 200) + 1 = 101} hlasů.
Pokud je hlasovací pravidlo respektováno, pak pro vítěznou m-člennou koalici Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1 \leq m \leq N)} platí:
Pokud výše uvedený vztah neplatí, tak se jedná o poraženou koalici, která nemá v současné chvíli šanci prosadit své zákony/návrhy v parlamentu.
Pro měření síly koalic ve hře N hráčů je možno použít koncepci charakteristické funkce. Pokud pro všechny koalice S hry ve tvaru charakteristické funkce platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S) = 0} nebo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S) = 1} , tak tuto hru označujeme jako prostá hra se zápisem (N,v). Vítězná koalice S má charakteristickou funkci Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S) = 1} , naopak funkci Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S) = 0} má poražená koalice S. Pokud ovšem rozšíříme prostý zápis hry o hlasovací pravidlo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N, v, \alpha)} , je pak takto definovaná charakteristická funkce označována jako hlasovací hra.[3]
Pro vysvětlení principu hlasovacích her je nutné brát v potaz následující tři předpoklady:
- Všichni zástupci jedné strany hlasují vždy jednotně.
- Vytvoří-li se v určité fázi hlasovacího procesu nějaká koalice stran, pak stejně jako v bodu 1, hlasují všichni členové této koalice jednotně.
- Je možné vytvořit libovolné koalice stran a všechny koalice jsou stejně pravděpodobné.
Řešením volebních her je Shapleyův-Shubikův index síly, který vypočítá index síly jednotlivých politických stran.
Shapley-Shubikův index síly
Tato modifikace původního Shapleyova vektoru/hodnoty vychází ze skutečnosti, že počet členů dané politické strany není dostatečným ukazatelem hlasovací síly, respektive jejich vlivu. Záleží na tom, jakou sílu (potenciál) má strana k vytvoření vítězné koalice. Tento index síly vyjadřuje přínos politické strany vzhledem ke všem koalicím, jejíchž může být členem. Jelikož charakteristická funkce hlasovacích her může nabývat hodnot 0 nebo 1, je vztah zjednodušen oproti původní verzi na:[3]
kde sumace probíhá přes všechny vítězné koalice S takové, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i \in S} a S-{i} je poražená koalice. Pro Shapleyovy hodnoty platí, že součet všech hodnot je roven jedné a zároveň je to nezáporné číslo. A jelikož je součet roven jedné, je možné využít Shapleyho index jako pravděpodobnost. A tato pravděpodobnost vyjadřuje, jak moc bude politická strana i nepostradatelná při tvorbě vítězných koalicí (všech teoreticky možných).
Příklad na Shapley-Shubikův index
Počítání Shapley-Shubikova indexu přes výše zmíněný vzorec znovu funguje, ale opět si ukážeme aplikaci vzorce na lépe zapamatovatelné technice.
Zadání příkladu: Předpokládejme český parlamentní systém, kde je celkem 200 poslanců a hlasovací pravidlo je rovno 0,5 tedy nadpoloviční většina. Ve hře existují tři politické strany, strana A má 95 poslanců, strana B má 85 poslanců a strana C má 20 zástupců. Nyní určíme, která strana má nepostradatelnou pozici při tvorbě koalic.[3]
Znovu si určíme všechny možnosti, jak se budou tvořit koalice v pořadí příchodů stran k jednání. Stejně jako u příkladu na Shapleyho hodnotu.
Postup určování Shapleyho indexu je zde trošku jiný, než u předchozího příkladu. Zde budeme hledat takzvaný pivotní bod, respektive pivotní politickou stranu. Tato strana určuje, jak jsou důležití při tvorbě dané koalice. Pivotní strana bude tedy ta, která pomůže přenést hlasování z neúspěšného na úspěšné. Ukažme si to na příkladu. Koalice A-B-C. Přichází strana A, která má 95 poslanců. To jim bohužel nestačí na schválení hlasování, proto přichází strana B. Ta přinese 85 poslanců a součet poslanců strany A a B je 180! Tato koalice je úspěšná, hlasování projde, tudíž pivotní stranou této koalice je strana B. Proto na průsečík této koalice a strany B zaneseme hodnotu 1, k ostatním hodnotu 0.
K procvičení projdeme ještě další řádek. Tentokrát se jedná a koalici A-C-B. Přijde strana A, přinese 95 poslanců. Jelikož to nestačí, přichází strana C. Ta přinese sice 20 poslanců, ale to stačí k tomu, aby hlasování prošlo. Proto v této koalici je pivotní strana strana C. Jedničku píšeme na průsečík strany C a dané koalice A-C-B. Toto provedeme i pro ostatní koalice, posléze spočítáme součet, kolikrát je strana pivotním bodem a podělíme tento počet počtem možných koalicí (příchodů stran).
| Postup tvorby koalice | Strana A | Strana B | Strana C |
|---|---|---|---|
| A-B-C | 0 | 1 | 0 |
| A-C-B | 0 | 0 | 1 |
| B-A-C | 1 | 0 | 0 |
| B-C-A | 0 | 0 | 1 |
| C-A-B | 1 | 0 | 0 |
| C-B-A | 0 | 1 | 0 |
| Shapleyův index Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i} | 2/6 (0,333) | 2/6 (0,333) | 2/6 (0,333) |
Pro všechny strany nám vyšel Shapleyho index stejný, tudíž v této hře jsou strany stejně nepostradatelné. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i = (2/6, 2/6, 2/6)} . Následně můžeme vypsat, jak dopadnou politické strany ve hře, pokud by tvořily různé koalice.
v({A}) = v({B}) = v({C}) = 0;
v({A,B}) = v({A,C}) = v({B,C}) = 1;
v({A,B,C}) = 1.
Slovním shrnutím, pokud by politické strany tvořily jednoprvkové koalice, ani jeden by neuspěl v hlasování. Pokud by dvě strany vytvořily koalici, hlasování bude úspěšné. To samé platí i pro koalici všech tří stran.
Informace o Shapleyho indexu
Dle řady vhodně zvolených experimentů se skutečné výsledky vyznačovaly značnou variabilitou a navíc se objevovaly těžce zdůvodnitelné rozdíly v konečných výhrách hráčů, kteří mají ve hře jinak naprosto symetrické postavení. Taktéž se stává, že hráč, který má dle Shapleyho indexu nejsilnější pozici, se slabším hráčům značně znelíbí a ve výsledku se dostane mimo všechny koalice a je možné, že by ho slabší jedinci, kteří jednají kolektivně přehlasovali.
Banzhafův index síly
Stojí za ním J. F. Banzhaf a použil ho v roce 1965. Značí se Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b = (\beta_1, \beta_2, ..., \beta_n)} . Jeho jednotlivé složky pro hráče 1, 2, ..., N jsou definovány vztahem:[3]
kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle e_i} značí počet koalic S, ve kterých je daná strana i nepostradatelná. Pro Banzhafův index platí to stejné, jako pro Shapleyho index a to, že jeho hodnota je nezáporná, součet všech Banzhafových indexů se rovná jedné a tento index lze použít jako pravděpodobnost.
Následně tedy koeficient Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta_i} vyjadřuje pravděpnost situace, kdy strana i může svým odstoupením anulovat vítězné postavení koalice.
Příklad na Banzhafův index síly
Při řešení příkladu na tento index, postupuje se obdobně, jako u Shapleyho indexu. Jako první a klíčová věc je nalézt všechny možné úspěšné koalice. Jinak řečeno, najít všechny kombinace politických stran v koalicích, které by uspěli v hlasování, při daném hlasovacím pravidlu.
Následně si vypíšeme všechny tyto koalice a začneme hledat kritické hráče dané koalice. Pro zrychlení jsou v následujícím příkladě již vybrány vítězné koalice. Zadání je následující: Existují čtyři politické strany, strana A má 12 členů, strana B má 6 členů, strana C má 4 členy a strana D má 2 členy. Hlasovací pravidlo není uvedeno, nýbrž je stanovena přesná hodnota 16 hlasů k úspěšnému hlasování.
Pokud chceme zjistit, jestli je daná politická strana kritickým hráčem, od součtu hlasů koalice odečteme počet hlasů jeho politické strany. Pokud po odečtení koalice nesplní počet hlasů nutných pro vítězství, je tato strana kritický hráč a na průsečíku koalice a hráče napíšeme jedničku. V číslech, pro první vítěznou koalici, která je složena ze stran A a B je celkový počet hlasů 18. Pokud chceme zjistit, zdali je strana A kritický hráč, odečteme od 18 počet hlasů strany A, tedy 12. Vyjde nám hodnota 6, která nesplňuje hlasovací kritérium, tudíž hlasování by neprošlo a strana A je kritický hráč. To samé provedeme i pro stranu B a zjistíme, že je na tom úplně stejně. Proto tedy mají v tabulce, v prvním řádku hodnoty jedna, které indikují, že jsou kritickými hráči. To samé provedeme i pro ostatní vítězné koalice.
| Vítězné koalice | Strana A | Strana B | Strana C | Strana D |
|---|---|---|---|---|
| A-B | 1 | 1 | - | - |
| A-C | 1 | - | 1 | - |
| A-B-C | 1 | 0 | 0 | - |
| A-B-D | 1 | 1 | - | 0 |
| A-C-D | 1 | - | 1 | 0 |
| A-B-C-D | 1 | 0 | 0 | 0 |
| Banzhafův index Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \beta_i} | 6/10 (0,6) | 2/10 (0,2) | 2/10 (0,2) | 0/10 (0,0) |
Z výsledků tedy můžeme tvrdit, že nejkritičtějším hráčem je strana A, která by v 60 procentech sabotovala hlasování a koalici by hlasování neprošlo. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b = (6/10, 2/10, 2/10, 0/10)} .
Příklady na procvičení
Kooperativní hra pro dva hráče
Existuje kooperativní hra dvou hráčů, jejíž výplatní matice je níže v tabulce 1i. Zjistěte celkovou maximální výhru při kooperaci, zkontrolujte jestli hra splňuje podmínky a vypočítejte výhru hráčů při:
Počítejte s tím, že je výhra přenosná! Dodatek: Zkuste zjistit, zdali by se hráčům vyplatila kooperace, pokud by výhra byla nepřenosná. |
| X | Y | |
|---|---|---|
| A | 3,-1 | -3,-2 |
| B | 7,2 | 1,5 |
Shapleyova hodnota
Existuje hra o třech hráčích. Jejich charakteristické funkce jsou následující: v({1}) = 80; v({2}) = 56; v({3}) = 70; Určete Shapleyovu hodnotu každého hráče. |
Shapley-Shubikův index síly
Banzhafův index síly
Existuje hlasovací hra se čtyřmi hráči. Strana A má 6 hlasů, strana B 4 hlasy, strana C 2 hlasy a strana D 1 hlas. Hlasovací kritérium pro úspěch hlasování je 9 hlasů. Vypočítejte Banzahafův index síly pro všechny čtyři strany. |
Výsledky příkladů
Kooperativní hra pro dva hráče
| X | Y | |
|---|---|---|
| A | 2 | -5 |
| B | 9 | 6 |
Maximální celková výhra kooperace je při strategii (B,X) a má hodnotu 9. Rovnovážná zaručená výhra je ve strategii (B,Y) s hodnotami (1, 5).
Doposud známé parametry:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1) = 1}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(2) = 5 }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) = 9 }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = 9 }
Při kooperační hře s přenosnou výhrou spočítáme možnosti výhry dle možností dělení celkové výhry:
- Každý hráč dostane polovinu celkové výhry kooperací:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = a_2 = \frac{9}{2} = 4,5}
- Každý hráč dostane zaručenou výhru a polovinu ze zbytku po kooperaci:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1* = 1 + \frac{[9 - 1 - 5]}{2} = 2,5}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2* = 5 + \frac{[9 - 1 - 5]}{2} = 6,5}
Z hlediska podmínek:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) > v(1) + v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 9 > 1 + 5} OK
- Každý hráč dostane polovinu celkové výhry kooperací:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = v(1,2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 4,5 + 4,5 = 9} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 \geq v(1)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 4,5 \geq 1} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 4,5 \geq 5} KO
- Každý hráč dostane zaručenou výhru a polovinu ze zbytku po kooperaci:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = v(1,2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,5 + 6,5 = 9} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 \geq v(1)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,5 \geq 1} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 6,5 \geq 5} OK
Ve výsledku hráč 2 by hru s přenosnou výhrou hrál za podmínky, že by se výhra dělila druhým způsobem, tedy zaručená výhra plus polovinu ze zbytku. Dělení celkové výhry na půl je pro něj nevýhodné!
Při kooperační hře s nepřenosnou výhrou by se Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 = 7} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 = 2 } a z hlediska podmínek:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(1,2) > v(1) + v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 9 > 1 + 5} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 + a_2 = v(1,2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3 + 5 = 8} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1 \geq v(1)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7 \geq 1} OK
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_2 \geq v(2)} čili Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2 \geq 5} KO
Hráč 2 by při nepřenosné výhře nehrál, jelikož by ho to znevýhodnilo.
Shapleyova hodnota
| Postup tvorby koalice | Hráč 1 | Hráč 2 | Hráč 3 |
|---|---|---|---|
| 1-2-3 | 80 | 0 | 10 |
| 1-3-2 | 80 | 5 | 5 |
| 2-1-3 | 24 | 56 | 10 |
| 2-3-1 | 18 | 56 | 16 |
| 3-1-2 | 15 | 5 | 70 |
| 3-2-1 | 18 | 2 | 70 |
| Shapleyova hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h_i} | 235/6 (39,166) | 124/6 (20,666) | 181/6 (30,166) |
Shapley-Shubikův index síly
K úspěšnému hlasování by bylo potřeba 121 hlasů. Proto by nastala změna v druhém, čtvrtém, pátém a šestém řádku. Ve druhém by nestačil součet strany A a C, to je pouze 115. Proto by se změnil pivotní bod na stranu B. To samé ve čtvrtém řádku, součet strany B a C by nestačil k úspěšnému hlasování, proto by pivotním bodem byla strana A. Taktéž u posledních dvou řádků. Ve výsledku by se změnil Shapleyho index, strana A a B by měly index 0,5 a strana C by v této hře byla naprosto zbytečná.
v({A}) = v({B}) = v({C}) = 0;
v({A,C}) = v({B,C}) = 0;
v({A,B}) = 1;
v({A,B,C}) = 1.
Banzhafův index síly
Vítězné koalice jsou následující: AB, ABC, ABD, ACD, ABCD. V nichž je strana A 5x kritický hráč, strana B 3x, strana C jednou a strana D taktéž jednou. Banzhafovy indexy jsou tedy b = (5/10, 3/10, 1/10, 1/10).
Reference
- ↑ 1.0 1.1 1.2 1.3 1.4 DLOUHÝ, Martin; FIALA, Petr. Úvod do teorie her. Praha : Nakladatelství Oeconomica, 2009. 119 s. ISBN 978-80-245-1609-7. S. 35-37.
- ↑ 2.0 2.1 Friebelová Jana: Teorie her, str. 15 [online]. Ekonomická fakulta Jihočeské univerzity [cit. 2016-06-11]. Dostupné z: http://www2.ef.jcu.cz/~jfrieb/rmp/data/teorie_oa/TEORIE%20HER.pdf
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 3.16 DLOUHÝ, Martin; FIALA, Petr. Úvod do teorie her. Praha : Nakladatelství Oeconomica, 2009. 119 s. ISBN 978-80-245-1609-7. S. 57-70.
Učební videa
Game theory: Coalitional games
Yale university: Game theory - cooperative games
Game theory: Cooperative games and Shapley value