Extensive form
Contents
Introduction
The normal form games give a representation of players that make decisions simultaneously. However, in these games, players do not have any information about the other players’ strategies when they make their own choice. However, in lots of different situations, players make their decisions depending of the past choices of other players (e.g. chess game, auctions, negotiation, etc.). To represent this kind of games, we can use the extensive form by implementing game trees. In this paper, we will first define the concept of extensive form game. After illustrating it with some concrete examples, we will describe the typology and the different variants that can exist in this kind of games. Fourth, we will analyze more in detail the notion of strategy. Finally, we will study how we can solve this kind of games by introducing the concept of backward induction.
Definition
An extensive form game will be composed by several main components:
- Players: more often we consider games with two players.
- Procedure: who moves when and what are the possible choices are questions that have to be defined in the game.
- Information: it is important to know if we are in a situation with perfect and complete information or not.
- History: is the sequence of actions taken by the players up to some decision point. A terminal history is a history that contains the action choices of all the players up until the point where the payoff is distributed.
- Payoffs: finally, it is crucial to determine the different payoffs in function of the decisions made.
Here, we use the game trees in order to represent the extensive form games. The decisions are made at the nodes included in the set X. There is also an initial node at which the game begins. Then, the game evolves from node to node depending on the players’ decisions. The game ends when a terminal node is reached (set Z). At this point, players receive a payoff corresponding to the terminal node. The preferences of players (i = 1…I) are represented by utility functions ui. When a player has to decide, he might not know exactly at which of the nodes it’s located. There are thus information sets (set of nodes that all belong to the same player and at all of which the same set of action is available). We can thus observe that this kind of games can be divided into smaller sub-games that represent sub-trees according to the different information sets.
Now that the background is set, let us express the extensive form games in a formal notation. Here, the methodology of Levin (2002) will be used:
- A set of players i = 1, …, I
- A finite set X of nodes that form the game tree, with Z ⊂ X being the terminal nodes.
- A set of functions that describe for each x ∉ Z,
- The player i(x) who moves at x.
- The set A(x) of possible actions at x.
- The successor node n(x, a) resulting from action a.
- Payoff functions ui : Z → ℜ assigning payoffs to players as a function of the terminal node reached.
- An information partition: for each x, let h(x) denote the set of nodes that are possible given what player i(x) knows. Thus, if x′ ∈ h(x), then i(x′) = i(x), A(x′) = A(x) and h(x′) = h(x).
We can also use the notation i(h) or A(h) to denote the player who moves at information set h and his set of possible actions.
Concrete examples
Entry game
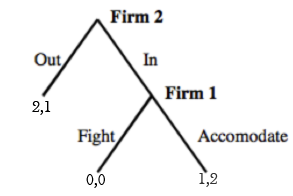
There is a firm M that has a monopoly on the market. Another firm E can decide to enter or not this market. If the firm E decides to enter the market, the monopoly firm can decide either to fight or to accommodate. The payoffs are the following: (2,0) if E does not enter; (-1, -1) if E enters and M fights and finally (1, 1) if E enters and M accommodates. The following game tree can represent it:
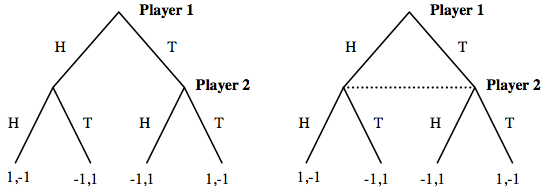
Matching pennies
We can also consider the matching pennies game. Here, the first player either chooses head or tail. The second player then also chooses head or tail. If both pennies have the same face, the second player wins; if not, the player 1 wins. A variant of this game can be that both players choose at the same time. The second player thus chooses without knowing the result of the first player (it is represented on the second graph). It is important to notice that the resulting payoffs are the same in both cases.
Typology
Perfect and complete information
It exists different types of extensive form games. Indeed, in some games, all the players know exactly each move of the others. The information is thus perfect and they can base their decision on the past moves of others. Moreover, if every player is aware of the entire tree (nothing is hidden or related to the chance), the game will be complete. For example, the chess game is perfect and complete. Indeed, each player knows the moves of the opponent and everyone knows all the possible moves they can achieve. It is also the case of the entry game explained above. In conclusion, all the information sets here is a singleton.
Imperfect information
Sometimes, it happens that one or several players do not get the perfect information. Indeed, it is possible that when a player has to decide, he does not know the past decision of the other player. In other words, a player sometimes cannot observe the choice of another player. Therefore, it means that moves can be simultaneous or a move could be hidden. The information set here will not be a singleton anymore. Graphically, it is represented by a dotted line connecting all the nodes of the information set (as on the tree of the variant of the matching pennies game). In conclusion, if a game is composed from at least one information set with more than one node, the game has imperfect information.
Incomplete information
In some games, it is also possible that some information is missing. For example, it is possible that a player does not know all the payoffs of the game. Some other information can also be missing: available nodes or decisions, the type or number of other players, the decision order, etc. In order to determine the type of the players, a so-called “nature” can be used (represented by a non-filled node) using a probability distribution. Here, each player observes his type but the other players do not. In conclusion, as we know that the payoff of the terminal node depends of the type of the player, nobody is sure about the payoff matrix. The game has thus incomplete information. An example of this is the auction game.
Finite or infinite games
A last typology can distinguish finite and infinite games. In the first case, there is a finite set of actions at each decision node. In the latter case, it can arise that at a decision node, there is an infinite number of possible actions. For example, if we have a Stackelberg competition, we can imagine that the decision node will be to define the quantity to produce. However, these quantities can take infinite value.
Strategies
A strategy is a complete contingent plan explaining what a player will do in every situation. Thus, for all the information sets, we can express the strategies as the different possible decision that the player can make.
Pure strategy
If we continue with the formal notation, we can define a pure strategy for a player i as a function si: Hi → Ai such that si(h) ∈ A(h) for each h ∈ Hi. Let Si denote the set of pure strategies available to player i, and S = S1 × ... × SI denote the set of pure strategy profiles. As before, we will let s = (s1, ..., sI ) denote a strategy profile, and s−i the strategies of i’s opponents. For example, if we take the entry game, here are the strategies of both players:
- S1=[out-fight; out-accommodate; in-fight; in-accommodate]
- S2=[in-out]
We can notice here that if we make a list of all players and their pure strategies, we can represent the extensive form game with its associated normal form.
Mixed strategy
A mixed strategy for player i in an extensive form game is a probability distribution over pure strategies, i.e. some σi ∈ ∆(Si). In a mixed strategy, the player randomly chooses at the beginning a pure strategy that he will use afterwards. When this strategy is chosen, he continues by following this deterministic rule of decisions.
Behavioural strategy
A behavioural strategy for player i in an extensive form game is a function σi : Hi → ∆(Ai) such that support(σi(h)) ⊂ A(h) for all h ∈ Hi. On the opposite, a behavioural strategy can be seen as stochastic. Indeed, here a random decision will be made at each decision node. Here, the hazard is focused on the next action and not on a global rule of behaviour as for mixed strategy.
There is a theorem linking these two types of strategies: the Kuhn’s Theorem. It says that if we have a game with perfect recall (i.e. players always remember past decision and information they had while making those decisions), mixed and behavioural strategies are equivalent. It means that there is an equivalent behavioural strategy for any mixed strategy.
Strategic form of extensive form games
In order to solve extensive form games, we can also use the concept of Nash equilibrium of the normal form, as explained above. We will also show in the next sections that it allows providing more detailed predictions (e.g. sub-game perfect equilibrium). Let us take again the entry game example. Gathering all the strategies, we can build the associated normal form as follow:
| Allow | Fight | |
| In | (2,1) | (0,0) |
| Out | (1,2) | (1,2) |
Therefore, now that we transformed the extensive form game, we can analyse it and see that there are two pure Nash equilibria (Challenge-Accommodate and Stay out-Fight). However, this is not completely right. Indeed, using the normal form, the Nash equilibria do not take into account the sequential structure of that game. It treats strategies as choices that are decided in one time and forever. Thus, we need an equilibrium that gives optimal strategies for all players not only at start but also at every moment of history. To do this, we first need to define the concept of sub-game.
Sub-game
A sub-game is a part of the game that can be seen as a game itself. It owns a single initial node and includes all the successive nodes starting from there. In other words, when the initial node of a sub-game is reached, players can focus only on it and forget the past history of the game. Again, we can give the formal notation of a sub-game: Let G be an extensive form game, a sub-game G′ of G consists of (i) a subset Y of the nodes X consisting of a single non-terminal node x and all of its successors, which has the property that if y ∈ Y, y′ ∈ h(y) then y′ ∈ Y , and (ii) information sets, feasible moves, and payoffs at terminal nodes as in G. Let us illustrate it with an example:
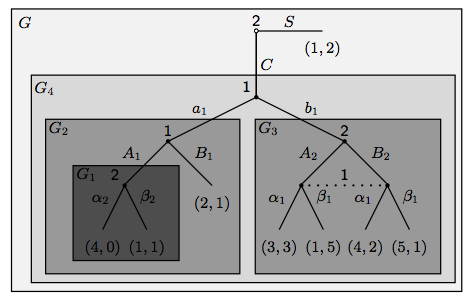
Here we can see that there are five different sub-games. First, there is the game itself (G). Second, we have a sub-game starting when C is selected at the first step (G4). Then, we have two different sub-games, depending of the decision of player 1 (G2 and G3). Finally, we have a last sub-game that includes the last decision of player 2. Doing this, we can refine the model and analyse if there is any sub-game perfect equilibrium. We can define a sub-game perfect equilibrium as follow (Selten, 1965): A sub-game perfect Nash equilibrium (SPNE) is a profile of strategies such that in each sub-game the induced strategy profile is a Nash equilibrium of that sub-game. Moreover, we can add that in every extensive form game there is at least one sub-game perfect equilibrium. Now we are therefore able to refine the Nash equilibria in order to define the more precise equilibria. To achieve this, we can use the backward induction methodology, describe in the following section.
Backward induction
Basically, the backward induction process is an iterative method in order to find the optimal strategies and Nash equilibria in extensive form or sequential games. The principle is quite simple: we first start by defining the optimal strategy of the player that makes the last move. Regarding this decision, we analyse the optimal strategy for the player that makes the previous move. In other words, what would he do knowing the optimal strategy of the other player. Finally, we continue this process till we reach the initial node. Doing this, we can determine the Nash equilibria of each sub-game of the original game. At the end, we will be able to define the sub-game perfect equilibrium.
Let us illustrate this with a new example. Consider the following game:
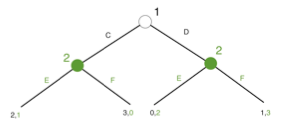
In this extensive form game, the first player chooses one action (C or D). Depending of this, the second player chooses his final action (E or F). The different payoffs are at the bottom of the graph. Here, we can see that we have three sub-games (the game itself and the two sub-games, depending on the player 1’s decision.
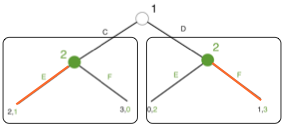
We start by analysing the two different sub-games. In the first one, if player 1 chooses action C, the second player will automatically choose the action E because it gives a better payoff (1 > 0). In the other sub-game on the opposite, if player 1 chooses D, the player 2 will choose action F for the same reason as the previously (3 > 2). Now that we have the optimal strategies for the last move, we can go upstream in order to find the optimal strategy of player 1. To do this, we compare his payoff in both situations. If he chooses the action C, the player 1 will get a utility of 2. In the other case, he will receive only 1. Player 1 will thus decide to take the action C because he knows that doing this, the second player will choose E and then he will get a better payoff. The strategy (C-E) is therefore the sub-game perfect equilibrium. In this case, it is the only sub-game perfect equilibrium. However the backward induction cannot be applied to every extensive form games. Indeed, sometimes if the game is infinitely long, it will be impossible to determine the sub-game perfect equilibria. However, it is possible to apply this methodology even if we have an imperfect information game.
Chance moves
A last concept that is important to stress out is that sometimes it is possible that chance nodes appear in the extensive form game. Indeed, depending on a choice, it is possible to reach different path according to a probability function.
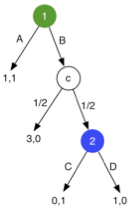
We can observe in this game that if the first player chooses the action B, we reach the chance node. There is 50% of chance that the game stops with a certain payoff (3,0) and 50% of chance that the second player has to make a final decision. Here, we can also apply the backward induction to find the sub-game perfect equilibrium. Let us start with the final sub-game. The second player will automatically choose action C because it gives a better payoff. Knowing this, the first player has two possibilities. First, he can choose action A and the game end with the payoff (1,1). Second, he can decide to go on the chance node. In this case, he has 50% chance to get a utility of 3 but 50% chance to receive nothing. The total utility is thus 50% of 3 + 50% of 0 = 1,5. This payoff is better than 1 if he chooses action A and will thus decide to take action B. The perfect equilibrium here is thus (A-C).
Exercises
- 1. Consider the following extensive form game:
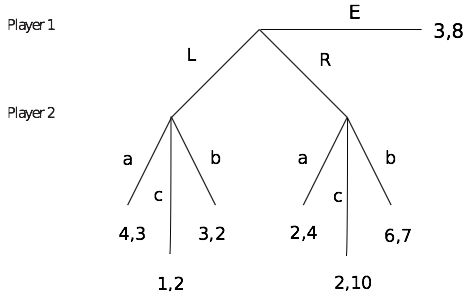
- a) Find all the Nash equilibria of the game
- b) Find all the sub-game perfect equilibria of the game
- 2. In an extensive form game two nodes are in the same information set whenever
- (a) They belong to different players and players cannot differentiate between them.
- (b) They belong to the same player and that player cannot differentiate be- tween them.
- (c) They belong to different players and players can differentiate between them.
- (d) They belong to the same player and that player can differentiate between them.
- (e) None of the above.
- 3. If we solve the following game with backwards induction, what is the resulting payoff?

References
- Lenaerts, T. (2012). Learning Dynamics, seen on http://ai.vub.ac.be/sites/default/files/Extensive%20form.pdf the 5th of January
- Levin, J. (2002). Extensive form games, seen on http://www.stanford.edu/~jdlevin/Econ%20203/ExtensiveForm.pdf the 4th of January
- Ratliff, J. (1997). Strategies in Extensive-Form Games, seen on http://www.virtualperfection.com/gametheory/4.2.StrategiesInExtensiveFormGames.1.0.pdf the 4th of January
- Von Stengel, B., Van Den Elzen, A., Talman D. (2002). Computing normal form perfect equilibria for extensive two-person games, Econometrica, Vol. 70, No. 2 (March), pp.693-715