Markov decision process/cs
Contents
Úvod
Nejistota je velice častým rysem obrovského množství modelů v různých oborech, od počítačové vědy, inženýrství a operačního výzkumu až po ekonomie. Často je nutné řešit problémy nebo přijímat rozhodnutí bez komplexních znalosti všech relevantních faktorů a bez znalosti jejich možného budoucího chování. Ve spoustě situacích výsledek částečně závisí na náhodnosti a částečně na rozhodování agenta. Proto je velice užitečné vytvořit rámec pro modelování toho, jak rozhodovat ve stochastickém prostředí. Příkladem takových modelů jsou Markovské procesy. Tyto procesy mají důležitou charakteristiku, která se spočívá v tom, že způsob, jakým se budou v budoucnu vyvíjet, závisí pouze na jejich současném stavu. To znamená, že každý proces je nezávislý na událostech z minulosti. Pomocí Markovských procesů lze modelovat celou řadu důležitých náhodných systémů, včetně biologických systémů a epidemiologie, finančních a fyzických systémů.[1]
Markovův rozhodovací proces (v angličtině Markov decision process nebo MDP) je matematický model pro rozhodování za nejistoty. Model se používá v situacích, kdy jsou výsledky částečně náhodné a zároveň částečně záleží na rozhodnutích [2]. MDP je obecnějším modelem (rozšířením) Markovských řetězců.[3] Hlavní rozdíl je v přidání do modelu užitků a akcí. V MDP agent provádí posloupnost akcí, které transformují stav systému do jednoho z několika možných následných stavů. Každý možný následný stav má určitou míru pravděpodobnosti přechodu.[4] Postup obsahuje zkoumání současného stavu a vykonaní akce. K řešení se obvykle používají algoritmy dynamického programování.[5] Avšak nevýhodou metod dynamického programování je ten fakt, že prohledávají celý prostor stavů. Takový přistup může být velice náročným vzhledem k času a zdrojům. Dalším problémem je “Short-term vs. long-term problem” – to, co je vhodné z krátkodobého hlediska, může být nevhodné z dlouhodobého hlediska.[2] Jedna z prvních publikací je “A Markovian Decision Process” z roku 1957, autorem je Richard Bellman. V současnosti MDP našlo uplatnění v různých disciplínách – robotika, automatické řízení, ekonomika, výroba atd.
Definice
V této časti se soustředíme na konkrétnější definici a matematický vzore. Nutné zmínit, že existují různé formulace pro MDP, avšak klíčové aspekty jsou stejné. V MDP existuje “tvůrce rozhodnutí“, který se nazývá agent. Agent interaguje s prostředím, ve kterém je umístěn. K těmto interakcím dochází postupně. V každém kroku agent získává určitou reprezentaci stavu prostředí. Vzhledem k této reprezentaci agent vybere akci, kterou má provést. Prostředí je poté převedeno do nového stavu a agent dostává odměnu v důsledku předchozí akce.
Komponenty MDP:
- Agent
- Prostředí
- Stav
- Akce
- Odměna
Proces výběru akce z daného stavu, přechodu do nového stavu a získání odměny se děje postupně znovu a znovu. Výsledkem je trajektorie/mapa, která ukazuje posloupnost stavů, akcí a odměn. V průběhu tohoto procesu je cílem agenta maximalizovat celkové množství odměn, které získává za provádění akcí. To znamená, že agent chce maximalizovat nejen okamžitou odměnu, ale kumulativní odměny, které dostává v průběhu času. Posledním nezbytným bodem je tranzitní (přechodová) funkce, která označuje pravděpodobnost přechodu z jednoho stavu do jiného při volbě určité akce.
Markovův rozhodovací proces pak může být definován jako uspořádaná čtveřice prvků {S, A, T, R}, kde
- S – značí konečnou množinu stavů.
- A – značí konečnou množinu akcí, pro každý stav je možno určit určitou množinu akcí.
- T – značí tranzitní (přechodovou) funkci nebo model, ve kterém T (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_t, a, S_{t+1}} ) je pravděpodobnost přechodu do stavu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{t+1}} při aplikaci akce na stav Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_t} .
- R – značí okamžitý užitek dosažený po přechodu ze stavu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_t} na stav Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_{t+1}} s pravděpodobností přechodu T (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_t , S_{t+1}} )
Agenti jen zřídka učiní jenom jedno rozhodnutí. Každé rozhodnutí má obvykle nějaké důsledky, vedoucí k dalším rozhodnutím, která vedou k dalším rozhodnutím atd. Cílem je vybrat strategii, která bude maximalizovat kumulativní funkci náhodných užitků. Metoda identifikující optimální strategii závisí na formě účelové funkce, tj. na optimalizačním kritériu. Volba vhodného kritéria závisí na povaze prostředí (např. jsou rozdílné při nekonečném nebo konečném horizontu)[5]
Algoritmy
Jelikož cílem MDP je poskytnout tvůrci rozhodnutí optimální politiku, která bude maximalizovat určitou kumulativní funkci odměn, v průběhu let vznikla řada metod. Avšak nejběžnějšími metodami, jak řešit Markovské rozhodovací procesy, jsou metody lineárního a dynamického programování. Právě metodám dynamického programování bude věnován následující text.
Přesné metody: Dynamické programování
Nejprve je třeba zavést několik předpokladů. Nechť je známa funkce přechodu a funkce odměny, takže cílem je získat politiku, která maximalizuje očekávanou diskontovanou odměnu. Algoritmus má jen dva druhy kroků, které jsou opakovány v určitém pořadí pro všechny stavy:
Iterace hodnot
Tento přistup navrhl Bellman v roce 1957 [4], přístup iterace hodnot, nazývaný také zpětná indukce. Algoritmus vypočítává očekávanou hodnotu každého stavu pomocí hodnoty sousedních stavů až do konvergence.
Iterace strategie
V této metodě se pracuje se vzorcem daném iterací hodnoty, pak se umožní strategii aktualizovat tak, že v akce provedená v každém stavu poskytuje minimální hodnotu pro nově vypočítané hodnoty sousedů tohoto stavu. Tento proces pokračuje, dokud existuje rozdíl mezi novou strategií a předcházející.[5]
Zpracování nejistoty: POMDP a přibližné metody
Hlavním předpokladem předchozích metod bylo to, že stavy jsou známé, stejně jako funkce distribuce akce. V reálném životě tomu tak často není. Zvláštní třída MDP – částečně pozorovatelný Markovův rozhodovací proces (POMDP) se zabývá případy, kdy aktuální stav není vždy znám.
Jiný druh nejistoty vzniká, když pravděpodobnosti nebo odměny nejsou známé. Populární oblastí, která se zabývá takovýmto problémem (zejména v oblasti umělé inteligence) je oblast zpětnovazebního učení. Síla zpětnovazebního učení leží v jeho schopnosti řešit Markovský rozhodovací proces bez výpočtu pravděpodobností přechodu.
Aplikace MDP
White, D.J. v článku Real Applications of Markov Decision Processes uvádí velký seznam aplikací:
- Zemědělství: kolik pěstovat na základě počasí a stavu půdy.
- Vodní zdroje: jak udržovat správnou hladinu vody v nádržích.
- Kontrola, údržba a opravy: kdy vyměnit/zkontrolovat na základě věku, stavu atd.
- Nákup a výroba: kolik vyrobit na základě poptávky.
- Fronty: zkrátit čekací dobu.
- atd.
Další příklady je možné najít v následujících publikacích: Markov Decision Processes with Applications to Finance, Have we met? MDP Based Speaker ID for Robot Dialogue, Training and evaluation of an MDP model for social multi-user human-robot interaction, Autonomous Exploration For Navigating In MDPs, The optimal game in 2048 with the help of the Markov decision-making process
V rámci tohoto článku bych chtěl uvést dva následující řešení. První příklad je z přednášek, ale má složitější formu než na stránkách prezentace.
Příklad 1
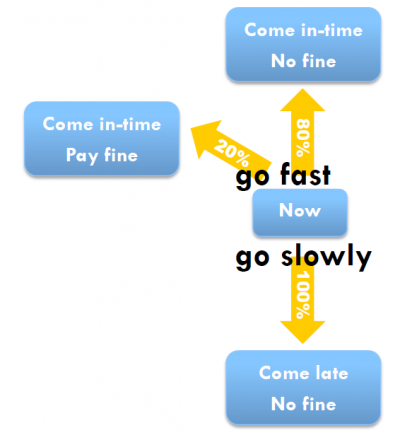
V původní verzi agent musí rozhodnou mezi 3 možnostmi (obrázek zprava grafické znázorňuje toto zadaní):
- jet pomalu, nedostat pokutu a přijet pozdě
- jet rychle, nedostat pokutu a přijet včas
- jet rychle, dostat pokutu a přijet včas (zanedbáváme v tomto případě časem, který agent ztratí při zastavení a placení pokuty; pokuta je důsledkem změření rychlosti)
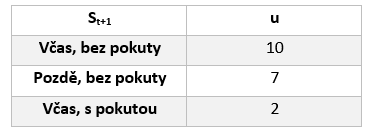
Užitky, které agent může dostat, ukazuje následující tabulka:
Nyní stačí rozhodnout, jak by měl agent jet – rychle nebo pomalu:
Pomalu: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {7*1}=7} (užitek je 7 a pravděpodobnost je 1)
Rychle: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {2*0.2+10*0.8=8.4}} (2 a 10 jsou užitky, 0.2 a 0.8 jsou pravděpodobnosti)
Jelikož Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8.4>7}
, agent by měl jet rychle.
Rozšířený příklad
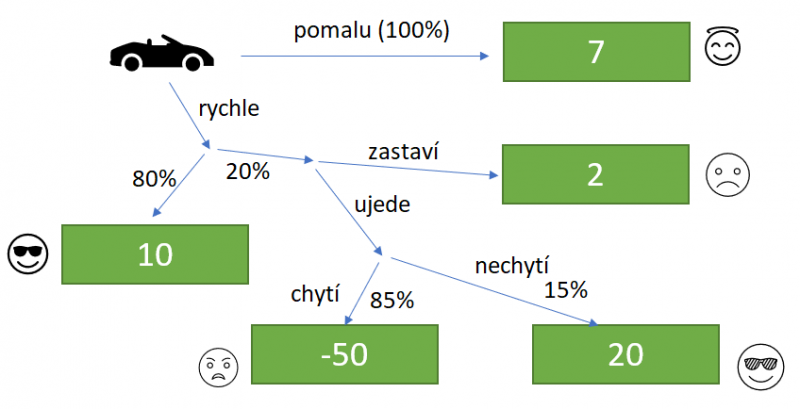
Do minulého zadaní můžeme přidat další rozhodnuti. Když agent bude jet rychle a bude změřen, bude mít dvě možnosti na výběr – zastavit se nebo ujet. V případě, že se pokusí ujet, mohou nastat dvě situace – chytí ho nebo nechytí. Následující schematický obrázek ukazuje základní body tohoto zadaní.
A{pomalu; rychle-zastaví; rychle-ujede} – seznam akcí.
O{pozdě-bez pokuty; včas-s pokutou; rychle-bez pokuty; rychle-bez pokuty-ujede; rychle-bez pokuty-chytí} – seznam stavů.
Pro každou akcí provedeme výpočty:
A(pomalu): Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7*1 = 7}
A(rychle-zastaví): Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2*0.2+10*0.8=8,4}
A(rychle-ujede): Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0.2*(0.15*20+0.85*(-50))+0.8*10=0.1}
Znovu správná strategie pro agenta jet rychle a v případě, že bude vyžádán – zastavit se.
Příklad 2
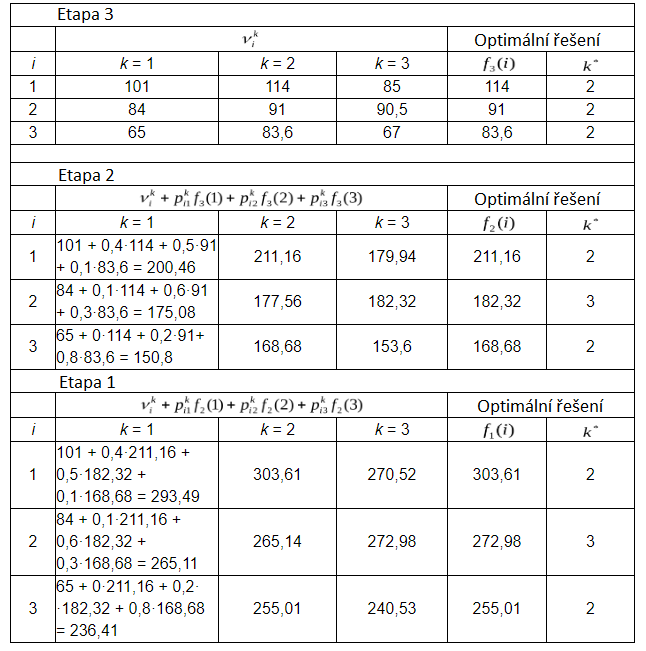
Obchod plánuje svou práci na tři měsíce, ředitel obchodu musí rozhodnout: jaká opatření mohou stimulovat poptávku. Má na výběr následující možnosti: sleva 3 % na příští objednávku, doprava zdarma nebo nedělat nic. Kromě toho společnost oceňuje měsíční tržby: výborně, velmi dobře, dobře.
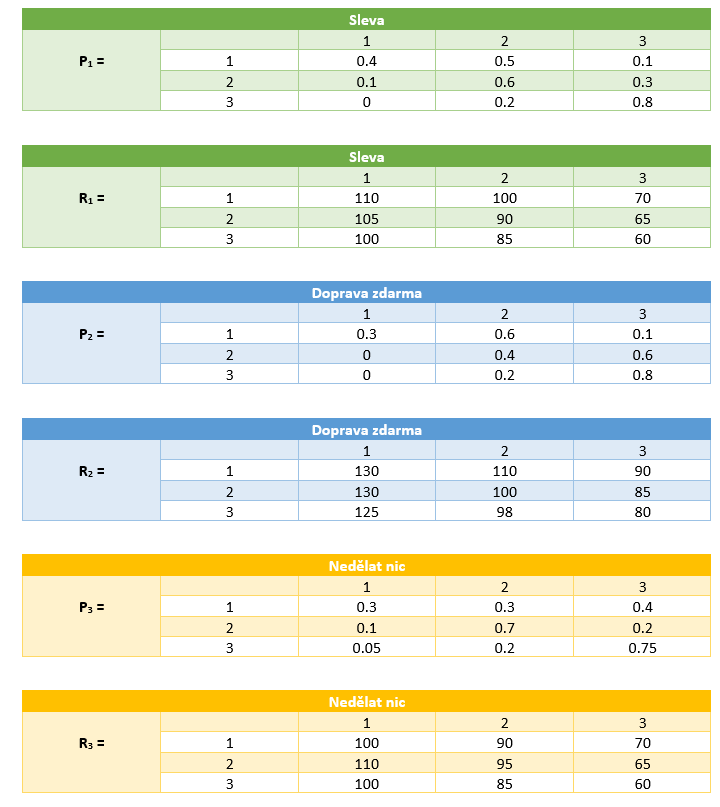
Jsou známé přechodné pravděpodobnosti a odpovídající měsíční příjmy pro každou možnost:
Cílem je najít optimální strategii pro stimulaci poptávky. V našem případě máme 3 měsíce a 3 úrovní poptávky (výborně, velmi dobře, dobře).
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_1^1=0.4*110+0.5*100+0.1*70=101}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_2^1=0.1*105+0.6*90+0.3*65=84}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_3^1=0*100+0.2*85+0.8*60=65}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_1^2=0.3*130+0.6*110+0.1*90=114}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_2^2=0*130+0.4*100+0.6*85=91}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_3^2=0*125+0.2*98+0.8*80=83.6}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_1^3=0.3*100+0.3*90+0.4*70=85}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_2^3=0.1*110+0.7*95+0.2*65=90.5}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \nu_3^3=0.05*100+0.2*85+0.75*60=67}
S ohledem na náklady každé strategie (10, 20, 0):
Optimální řešení ukazuje, že v prvním a druhém měsíci by společnost měla stimulovat poptávku pomocí bezplatného doručení (pokud poptávka bude “výborná” nebo “velmi dobrá”). Pokud je poptávka jen “dobrá“, nemělo by se nic dělat. Ve třetím měsíci by měl obchod zajistit dodání zdarma bez ohledu na stav systému.
Závěr
MDP je zajímavá a přínosná metoda, kterou je možné používat v obrovském množství situací. Avšak musím zmínit to, že pro dostačující pochopení základů a různorodých metod, člověk musí věnovat tomu hodně času.
Zdroje
Reference
- ↑ 1.0 1.1 1.2 ZANINI, Elena. Markov Decision Processes. [online] [cit. 2020-06-01] Dostupné z: https://www.lancaster.ac.uk/postgrad/zaninie/MDP.pdf/
- ↑ 2.0 2.1 ŠALAMON, Tomáš. Podklady k předmětu 4IT495 - Simulace systémů; VŠE - fakulta informatiky a statistiky. 10-Multiagent_systems_I_.pdf
- ↑ TŮMOVÁ, Jana. Paralelní ověřování kvalitativních vlastností pravděpodobnostních modelů. Brno,2006. Masarykova Univerzita, Fakulta informatiky. Vedoucí práce: Mgr. Jiří Barnat, Ph.D.
- ↑ 4.0 4.1 IBE, Oliver. Markov Processes for Stochastic Modeling. Saint Louis: Elsevier. 2013. ProQuest Ebook Central
- ↑ 5.0 5.1 5.2 STÁREK, Ivo. Plánování cesty robota pomocí dynamického programování. Brno,2009. Vysoké učení technické v Brně, Fakulta strojního inženýrství. Vedoucí práce: RNDr. Jiří Dvořák, CSc.
Doplňující literatura
Piunovskiy, Alexey B. 2012. Examples In Markov Decision Processes. Singapore: World Scientific Publishing Company. ProQuest Ebook Central.
Feinberg E., Shwartz A. 2012. Handbook of Markov decision processes: methods and applications. Springer-Verlag New York Inc.
Videa
Coursera - Markov Decision Processes
Markov Decision Processes (MDPs) - Structuring a Reinforcement Learning Problem

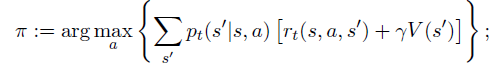
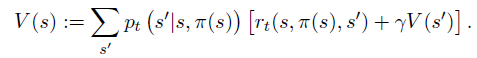
![Algoritmus převzat z článku[1]](/images/IteraceHodnot.PNG)
![Algoritmus převzat z článku[1]](/images/IteraceStrategie.PNG)