Multiagentní simulace ne/platících cestujících MHD skrze kostru PPGwP
Tato stránka je slouží jako Výzkumná zpráva simulace "Multiagentní simulace ne/platících cestujících MHD skrze kostru PPGwP" k semestrálnímu projektu pro předmět 4IT495 Simulace systémů (LS 2012/2013) na VŠE v Praze.
Zadání
- Název simulace: Multiagentní simulace ne/platících cestujících MHD skrze kostru PPGwP
- Předmět: 4IT495 Simulace systémů (LS 2012/2013)
- Autor: Filip Svatoš
- Typ modelu: Multiagentní simulace
- Modelovací nástroj: NetLogo
Detailní zadání viz stránka pod odkazem: User_talk:Xsvaf02
Stručné zadání
Agenti budou "hrát" modifikaci PGGwP aplikovanou na problém černých pasažérů. Návaznost PGGwP na reálnou situaci ČP v MHD vidím následovnou:
- Jedna se o veřejnou 'službu', kterou využívají všichni (platící i neplatící) a všichni z ní mají stejný užitek. Tato vlastnost je obdobná v laboratorní hře i v realitě.
- Výplata z PGG se dá ve realitě chápat jako získání užitku z využité služby (všichni mají z použití MHD stejný užitek - přesun z bodu A do bodu B v určitém čase a v určité kvalitě). Poníženi užitku(výplaty) při nárůstu počtu ČP se dá chápat jako zpomaleni dopravy (přeplněné MHD, více kontrol revizory) nebo zhoršení kvality dopravy (nejsou peníze na údržbu vozů).
- Koeficient násobení veřejného konta bude nastaven jako konstanta 2. Agenti v modelu nejednají za primárním účelem maximalizovat zisk a navíc je rozhodnutí o placení pouze binární (zaplatí/nezaplatí), nelze tedy agenty motivovat k vyšším příspěvkům. Hodnota majetku je zde pouze pro účely porovnávání strategií a efektivity nastaví simulace. Koeficient je tedy potřeba mít > 1, aby mohli být zisky kladné a větší koeficienty pouze snižují škody způsobené ČP. Při množství agentů v simulaci je nežádoucí, jelikož by nebyl jejich nárůst tak dobře vidět v grafech.
- Trestáni je v simulaci placeno agenty - v realitě tento vztah nejde přímo vidět. Můžeme ho ovšem chápat jako ochotu agentů snížit svůj užitek za účelem zvýšení šance na potrestání ČP. Majetek agentu ze kterého se 'platí' tresty koneckonců nejsou jen peníze, ale i užitek získaný používáním MHD - např. časová úspora nebo pohodlí - investice do trestání může být brána jako ochota agentů podstoupit vice kontrol revizorem.
Definice problému
Černý pasažér v MHD
V práci uvažuji o MHD v Praze. Za černého pasažéra považuji cestujícího, který se vědomě a dobrovolně rozhodl nezakoupit jízdenku. Jejich reálné množství v pražské hromadné dopravě se odhaduje na 5 – 10%.
Dostupné odhady počtu černých pasažérů:
| Zdroj | Udávaný počet ČP |
|---|---|
| Eva Markytánová (BP, VŠE)[1] | 3,3 - 4,7% |
| Pavlína Froňková (BP, VŠE)[2] | 4 - 5% |
| Monika Jarolímová (BP, VŠE)[3] | 4 - 5% |
| iDNES.cz[4] | 5 - 7% |
| Trolejbusy v Praze[5] | 5,87% |
| Kraus, Kočí (ČVUT FD)[6] | přibližně 8% |
| Finmag[7] | 10% |
| lidovky.cz (Deloitte[8])[9] | 8 - 11% v metru a 11 - 13% v povrchové dopravě |
Hra na veřejné blaho
Hra na veřejné blaho, neboli public good game, je standardní ekonomická hra[10]. V základní verzi se jedná o skupinovou hru, ve které každý z hráčů dobrovolně vloží částku, kterou si sám zvolí, do společného konta. Tato částka se poté vynásobí číslem větším než 1 a rozdělí rovnoměrně mezi všechny hráče (nehledě na jejich vklad). Jedno z možných rozšíření je zavedení trestání. Po rozdělení částky z veřejného konta se hráči můžou rozhodnout, zda někoho potrestají. Trestají konkrétního hráče a za každý peníz, který na trestání vynaloží, se potrestanému strhne určitá částka z majetku. Další varianty hry zde nezmiňuji ani nepoužívám.
Cíl práce
Cílem práce je porovnat model založený na teorii her s realitou, zjistit zda je schopen věrohodně simulovat realitu, predikovat dopady změn, jeho slabá a silná místa, zanalyzovat chování agentů za různých nastavení a ověřit aplikovatelnost těchto zjištění zpět do reality.
Metoda
Pro simulaci jsem použil multiagentní přístup, zejména proto, že dovoluje tvorbu heterogenních agentů a umožňuje sledovat interakce agentů. Model je realizován v modelovacím multiagentním prostředí NetLogo. Agenti jednají vždy simultánně a v diskrétních časových úsecích (v prostředí NetLogo je tento diskrétní časový úsek nazván tick). Jeden tick znamená jedno celé kolo hry na veřejné blaho, včetně trestání. Ostatní přístupy
Studie o důvodech chování černých pasažérů jsem nenalezl. Vycházím tedy z dostupných popisů dat o černých pasažérech a osobnímu vnímaní problematické situace. Hru na veřejné blaho jsem pro tento problém zvolil z důvodu mnoha podobností mezi hrou a realitou (viz zadání).
Model
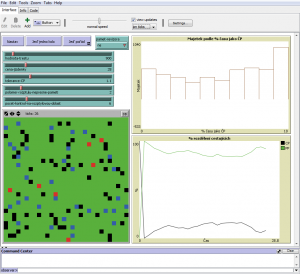
Popis prvků, prostředí a ovládání modelu
Svět modelu, zobrazený na obrázku č. 1, je obdélník o rozměrech 30x30 patches (možné souřadnice 0-29 xcor/ycor s počátkem v levém spodním rohu). Velikost modelu se dá libovolně měnit, příslušné posuvníky pro vstupní parametry se automaticky přizpůsobují velikosti světa. Model je ovšem výpočetně náročný, je tedy potřeba zvážit jak velký svět je příslušný stroj schopen zvládnout.
V prostředí jsou vidět pouze cestující. Jeden agent cestujícího je realizován jako jeden patch. Agent revizora je neviditelný. Agenti cestujících můžou nabýt čtyř stavů:
- ČP – černý pasažér – černá barva agenta
- PČP – potrestaný černý pasažér – červená barva agenta
- PP – platící pasažér – zelená barva agenta
- PPP – zkontrolovaný platící pasažér – modrá barva agenta
V prostředí se dále nachází 3 tlačítka, 5 posuvníků, 1 záložka pro výběr a 2 grafy. Zde je jejich popis:
- Tlačítko Nastav – slouží pro spuštění metody setup, která nastaví prostředí pro běh simulace
- Tlačítko Jeď jedno kolo – slouží pro jednorázové spuštění metody go, která provede jedno kolo běhu simulace
- Tlačítko Jeď pořád – slouží pro opakované spouštění metody go, čímž bude simulace běžet až do opětovného zmáčknutí tlačítka (vypnutí běhu simulace)
- Záložka pro výběr pamet-revizora – slouží k nastavení druhu paměti revizora (žádná, nepřesná, přesná)
- Posuvník hodnota-trestu – slouží k nastavení parametru velikosti trestu (možné hodnoty: 100 – 10000, hodnota inkrementace 10)
- Posuvník cena-jizdenky – slouží k nastavení parametru ceny jízdenky (možné hodnoty: 10 – 100, hodnota inkrementace 1)
- Posuvník tolerance-CP – slouží k nastavení parametru tolerance k černým pasažérům (možné hodnoty: 0,5 – 3, hodnota inkrementace 0,1)
- Posuvník polomer-rozptylu-nepresne-pameti – slouží k nastavení parametru rozptylu nepřesné paměti revizora (možné hodnoty: ( 1 – ( max-pxcor + 1 ) / 4 ), hodnota inkrementace 1)
- Posuvník pocet-kontrol-na-rozptylovou-oblast – slouží k nastavení parametru množství kontrol na jednu oblast nepřesné paměti revizora (možné hodnoty: 1 – ( (polomer-rozptylu-nepresne-pameti * 2 ) + 1 ) * ( (polomer-rozptylu-nepresne-pameti * 2 ) + 1 ), hodnota inkrementace 1)
- Graf Majetek podle % času jako ČP – zobrazuje průměrné množství majetku u skupin agentů rozdělených do decilů podle doby, kterou strávili jako černí pasažéři (sloupec úplně vlevo jsou agenti, kteří strávili ve stavu ČP nejméně času, obdobně sloupec úplně vpravo jsou agenti, kteří strávili ve stavu ČP nejvíce času)
- Graf % rozdělení cestujících – zobrazuje procentuální rozdělení agentů na černé a platící pasažéry v čase.
Popis logiky modelu
Implementovaná verze hry na veřejné blaho je od originální verze odlišná. V použité verzi se agenti rozhodují tajně (informace o tom, kolik který agent vložil do veřejného konta, není známa) a pouze mezi vkladem plné hodnoty jízdenky do veřejného konta nebo vložením ničeho (nezaplacení jízdenky). Z důvodu, že agenti se nerozhodují, kolik do veřejného konta vloží, ale pouze jestli vloží, je multiplikátor nastaven na základní hodnotu 2. Trestání zde není prováděno přímo, ale skrze pomocnou entitu revizora. Agenti se pouze rozhodují, kolik chtějí do trestání přispět ze svého majetku. Nemůžou si vybrat, koho přesně budou trestat, jelikož je hra tajná a neví tedy, kdo byl černý pasažér a kdo ne. Na základě takto vyjádřeného zájmu o trestání poté revizor provádí na základě nastavené strategie kontroly agentů a v případě, že takto odhalí černého pasažéra, potrestá ho. Trestání je tedy nepřímé a nepřesné. Posloupnost akcí, které za jedno kolo agenti simultánně provádějí, je následující:
- Nejprve se agenti rozhodnou, zda budou podvádět, nebo zaplatí jízdenku
- Po zaplacení všemi se částka vynásobí a rozdělí mezi agenty
- Na základě stavu hry se agenti rozhodnou, jestli budou trestat, a případně vloží danou hodnotu do konta revizora
- Revizor na základě obdržené částky provede kontroly a potrestá nalezené černé pasažéry
- Nakonec agenti na základě průběhu kola zaktualizují své tendence k podvádění do příštího kola.
Rozhodnutí agentů o podvádění je dáno pravděpodobnostní hodnotou každého agenta. Tato hodnota se aktualizuje na konci každého kola podle průběhu posledního kola. Na začátku je tato hodnota nastavena na nulu, model se při neextrémním nastavení velice rychle stabilizuje. Pravděpodobnostní hodnota podvádění je u jednotlivých agentů odlišná na základě jejich lokální zkušenosti. Na obrázku č. 2 je zobrazen vzorec pro výpočet pravděpodobnosti podvádění. Je to aritmetický průměr hodnoty podvádění za předchozí kolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho_{0}}
a hodnoty podvádění za současné kolo. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle J}
značí rovnovážnou pravděpodobnost počítanou z ceny jízdenky a hodnoty trestu, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \check{C}}
značí množství černých pasažérů, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P}
značí procento dopadených černých pasažérů, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R}
značí aktivitu revizora v okolí agenta, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Z}
značí osobní zkušenost agenta s revizorem.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho =\frac{{\rho }_{0}+\left(J+\check{C}-P-R+Z\right)}{2}}
Obrázek č.2: Vzorec pro výpočet pravděpodobnosti podvádění
Výpočet hodnoty J je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{\mathit{CJ}+\mathit{CJ}}{\mathit{CJ}+\mathit{CJ}+T}} . Jedná se o rovnovážnou pravděpodobnost založenou na Tsebelisově[11] herně teoretickém přístupu[12]. Hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \check{C}} je procento černých pasažérů ze všech cestujících. Hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} je procento potrestaných černých pasažérů. Hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R} je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left({\mathit{pPP}}_{M}{+\mathit{p\check{C}P}}_{M}\right)\ast \mathrm{0,0625}} . Hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pPP_{M}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p\check{C}P_{M}} značí počet potrestaných platících a černých pasažérů v Moorově sousedství, tedy okolních osm agentů od počítajícího agenta. Hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Z} je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathrm{0,5}} , pakliže je agent nepotrestaný černý pasažér a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle -\mathrm{0,5}} , pakliže je agent potrestaný černý pasažér. Hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Z} jsou hodnoty lokální a „subjektivní“ a jsou kalibrované tak, aby dohromady dávaly maximální možnou změnu 100%, neboli 1 (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8\ast \mathrm{0,0625}+\mathrm{0,5}} ). Agent jimi vnímá blízké okolí a silně z nich čerpá pro své rozhodování a simulují tak dostupnostní heuristiku[13]. Hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle J} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \check{C}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} jsou globální a „objektivní“.
Výpočet trestání je zobrazen na obrázku č. 3. Jedná se opět o aritmetický průměr hodnoty trestání z předchozího kola Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tau_{0}} a hodnoty trestání za současné kolo. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \check{C}P} značí počet černých pasažérů, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle C} značí počet všech cestujících a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} značí toleranci k černým pasažérům. Tolerance k černým pasažérům je vstupní nastavitelná proměnná. Tolerance černých pasažérů v podstatě říká, kolik kontrol bude za jednoho černého pasažéra provedeno. Větší tolerance značí méně kontrol.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \tau =\frac{{\tau }_{0}+{\left(\frac{\mathit{\check{C}P}}{C}\right)}^{T}}{2}}
Obrázek č.3: Vzorec pro výpočet pravděpodobnosti trestání
Agent může trestat i vícekrát, po každém rozhodnutí trestat se mu však snižuje šance na další trestání o 10%. Cena za jedno trestání je čtvrtina hodnoty jízdenky. Jedno agentem zaplacené trestání dá revizorovi jednu šanci ke kontrole.
Entita revizora provede tolik kontrol, kolik šancí mu agenti zaplatili. Revizor funguje ve třech možných nastaveních. První nastavení je revizor bez paměti. V tomto nastavení revizor kontroluje agenty zcela náhodně. V nastavení s přesnou pamětí si revizor pamatuje přesné umístění černých pasažérů nalezených v předchozím kole a tyto kontroluje přednostně. Po zkontrolování všech známých černých pasažérů kontroluje opět náhodně. Třetí nastavení je revizor s nepřesnou pamětí[14]. Zde lze nastavit dva parametry – rozptyl paměti a počet kontrol na oblast. Rozptyl paměti určuje poloměr okruhu od nalezeného černého pasažéra, ve kterém revizor tohoto černého pasažéra náhodně hledá. Vyšší číslo značí horší paměť revizora. Počet kontrol na oblast značí, kolik kontrol v této jedné oblasti revizor provede. Revizor po zkontrolování všech těchto oblastí kontroluje opět náhodně. Pakliže revizor černého pasažéra nalezne, strhne mu z majetku hodnotu trestu.
Vstupní nastavitelné parametry jsou cena jízdenky, hodnota trestu, tolerance ČP, druh paměti revizora, rozptyl nepřesné paměti a počet kontrol v oblasti. V modelu je 900 agentů. Toto číslo je libovolně nastavitelné, ovšem z důvodu výpočetní náročnosti jsem zvolil takto relativně nízké číslo.
Popis procedur
- Procedura vytvor-agenty – vytváří agenty cestujících a nastavuje počáteční hodnoty jejich parametrů.
- Procedura vytvor-revizora – vytváří agenta revizora a nastavuje počáteční hodnotu jeho parametrů
- Procedura aktualizuj-podvadeni – slouží pro výpočet pravděpodobnosti podvádění pro jednotlivé agenty
- Procedura rozhodni-podvadeni – na základě pravděpodobnosti podvádění rozhodne, zda bude konkrétní agent podvádět
- Procedura aktualizuj-trestani – slouží pro výpočet pravděpodobnosti trestání pro jednotlivé agenty
- Procedura rozhodni-trestani – na základě pravděpodobnosti trestání rozhodne, zda bude konkrétní agent trestat a případně rovnou zaplatí za trestání
- Procedura zahraj-kolo – řídí první část jednoho kola hry na veřejné blaho – tedy vložení majetku do veřejného konta a jeho následné rozdělení mezi hráče
- Procedura proved-trestani – zjistí jakou paměť má revizor zapnutou a spustí příslušnou proceduru
- Procedura trestat-nahodne [ pamet? ] – řídí náhodné kontrolování cestujících, vstupní parametr slouží pro vypnutí/zapnutí funkce ukládání nalezených černých pasažérů do paměti
- Procedura trestat-s-pameti [ rozptyl pocet-kontrol-na-oblast ] – řídí kontroly na základě paměti revizora, vstupní parametry slouží pro nastavení rozptylu paměti a počtu kontrol na oblast (pro přesnou paměť revizora jsou vstupní parametry rozptyl: 0, pocet-kontrol-na-oblast:1)
- Procedura zkontroluj [ x-souradnice y-souradnice p ]; - provádí samotné kontrolování, vstupní parametry jsou x/y souřadnice a parametr p, udávající, zda je zapnuta funkce ukládání nalezených černých pasažérů do paměti
- Procedura aktualizuj-barvu – je pomocná funkce pro aktualizaci zobrazovaných barev agentů podle stavů, ve kterém se nacházejí
- Procedura aktualizuj-pomocne-promenne – je pomocná funkce, ve které se dopočítávají pomocné hodnoty pro zobrazování grafu % rozdělení cestujících
- Procedura to-report random-rovnomerne – navrací náhodnou hodnotu 0-1 z rovnoměrného rozložení
Výsledky
Prováděl jsem několik pozorování, hlavní část výsledku však těží z dat vygenerovaných experimentem. Experiment proběhl pro celkem 252 různých nastavení, pro každé nastavení proběhlo 25 opakování, dohromady se jednalo o 6300 celkových opakování a každé opakování běželo 50 kol (ticků)[15]. Nastavení vstupních parametrů pro experimenty bylo následující:
| Jméno parametru | Hodnota parametru |
|---|---|
| cena jízdenky | 20, 30, 40, 50 |
| hodnota trestu | 500, 1000, 2000 |
| tolerance ČP | 0,5, 1, 1,5 |
| druh paměti revizora | bez paměti, s přesnou pamětí, s nepřesnou pamětí |
| rozptyl nepřesné paměti (pouze u nastavení s nepřesnou pamětí) | 2, 4 |
| počet kontrol v oblasti | 5, 20, 50 (pouze u hodnoty rozptylu 4) |
Pro zobrazení vlivů jednotlivých parametrů a srovnání modelu s realitou jsem uvažoval toto nastavení:
| Jméno parametru | Hodnota parametru |
|---|---|
| cena jízdenky | 30 |
| hodnota trestu | 1000 |
| tolerance ČP | 1 |
| druh paměti revizora | s nepřesnou pamětí |
| rozptyl nepřesné paměti (pouze u nastavení s nepřesnou pamětí) | 2 |
| počet kontrol v oblasti | 5 |
Při tomto nastavení je procento černých pasažérů 7,94%. Toto číslo může odpovídat realitě.
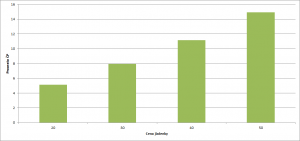
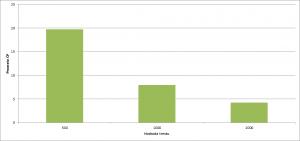
Vliv ceny jízdenky a hodnoty trestu
Vliv ceny jízdenky a hodnoty trestu se podle očekávání ukázal jako významný. Na obrázku č. 4 je vidět vliv ceny jízdenky a na obrázku č. 5 hodnoty trestu na procento černých pasažérů. Je zde je vidět silnější vliv hodnoty trestu na procento černých pasažérů, zejména pro příliš nízké hodnoty trestu (500), kdy je procento černých pasažérů více než dvojnásobné (19,75%) oproti hodnotě trestu 1000 (7,94%).
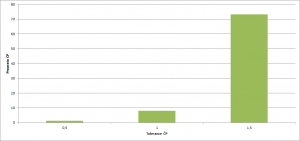
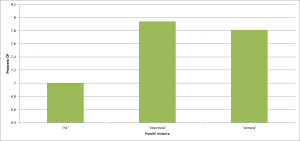
Vliv tolerance ČP
Velmi silný vliv se ukázal u tolerance černých pasažérů. Na obrázku č. 6 je vidět vliv tolerance černých pasažérů. Vliv silné netolerance je silný (1,26% oproti 7,94% černých pasažérů při toleranci 1). Ale vliv silné tolerance je mnohem silnější (73,22% černých pasažérů). Hodnota tolerance 1 může odpovídat realitě.
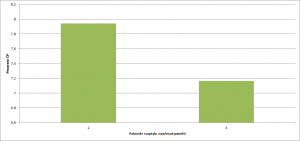
Vliv paměti revizora
Na obrázku č. 7 je vidět vliv paměti revizora. Nejlépe si vedla žádná paměť, ale výsledek není tak silný (7% oproti 7,94% černých pasažérů u nepřesné paměti). Přesná paměť si vedla obdobně jako nepřesná.
Důvodem, proč nepřesná paměť podává tak špatné výsledky, je, že krátkodobě sice vyčistí kontrolovanou oblast od černých pasažérů, ti se ovšem přesunou do nekontrolovaných oblastí, kde se jim daří. Začíná tak hra na kočku a na myš. Tento efekt jde dobře vidět obrázku č. 8 a 9, kde na obrázku č. 8 je pole s žádnou pamětí revizora a na obrázku č. 9 pole s nepřesnou pamětí. Kontroly (modrá a červená políčka) jsou u žádné paměti rozmístěné náhodně a udržují tak agenty mimo stav neplacení. Při nepřesné paměti jsou kontroly cílené na oblasti, kde byli odhalení nějací černí pasažéři. Tato strategie za sebou zanechává oblasti očištěné od černých pasažérů (například oblast nahoře uprostřed), ale černí pasažéři se přesouvají do jiných oblastí, kde se jim nadále daří a jejich celkový počet se tak zvedá. Tato strategie může odhalit největší počet černých pasažérů, ale má negativní dopad na prevenci vzniku černých pasažérů.
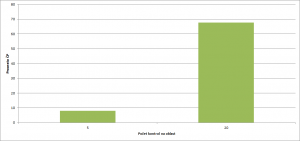
Vliv rozptylu a počtu kontrol na oblast paměti
Na obrázku č. 10 je vidět vliv poloměru rozptylu na efektivnost nepřesné paměti, na obrázku č. 11 je vidět vliv počtu kontrol na jednu oblast nepřesné paměti. Výsledky ukazují, že hlavním zdrojem neefektivity nepřesné paměti je právě počet kontrol v dané oblasti (intenzita kontrol v oblasti s nalezenými černými pasažéry). Klesající procento černých pasažérů při zvyšujícím se rozptylu paměti přisuzuji tomu, že se zvyšujícím se rozptylu nepřesné paměti se metoda kontroly blíží k trestání náhodnému (náhodné trestání se dá popsat jako trestání s nepřesnou pamětí s nekonečným rozptylem a nekonečným počtem kontrol na oblast).
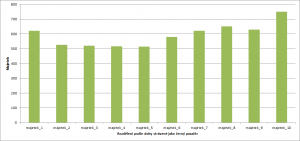
Ekonomická výhodnost černé jízdy
Nyní se podívám na výsledky modelu z pohledu cestujícího. Prosím čtenáře, nechť tyto výsledky bere se značnou rezervou. Model byl tvořen zejména pro simulaci počtu černých pasažérů v populaci. Toto je spíše zajímavý bonus navíc. Na obrázku č. 12 je vidět průměrné množství majetku agentů rozdělených podle doby, jakou strávili jako černí pasažéři. Vlevo je decil s nejmenší dobou (majetek_1) a vpravo s největší dobou (majetek_10) strávenou jako černý pasažér. Jde vidět, že celkově je nejvýhodnější jezdit na černo co nejčastěji. Podle modelu si agenti v decilu s nejdelší dobou strávenou jako černý pasažér vydělali přibližně o 21% více než agenti v decilu s nejkratší dobou strávenou jako černý pasažér. Zajímavé je, že se jízda na černo vyplácela až od sedmého decilu, výrazněji ale až v desátém decilu. Ostatní decily na tom byli hůře, než první decil.
Závěr
Model se ukázal jako schopný simulovat přibližně reálné hodnoty černých pasažérů. Jelikož reálné hodnoty nejsou k dispozici, nemůžu říct, jak přesný je můj model. Při nastavení přibližně odpovídajícímu realitě bylo v modelu okolo 7,94% černých pasažérů. Tato hodnota se může porovnávat s hodnotami z různých průzkumů uvedených v kapitole 2, které se pohybovaly od 5 do 13%. Důležitým výsledkem je také vliv nepřesné paměti revizora na chování černých pasažérů, kteří se přesunovali do oblastí, kde kontroly neprobíhaly. Nejsilnější vliv měly parametry druh paměti a tolerance černých pasažérů.
Velkou slabinou modelu je velké zjednodušení reality, což je prostor pro další rozšiřování a zpřesňování modelu do budoucna. Možným směrem dalšího vývoje je přesun pozornosti při rozhodování o podvádění k subjektivním pocitům agenta. Problém tohoto přístupu je, že je těžké jej exaktně a vědecky uchopit, jelikož je obtížné subjektivní pocity kvantifikovat.
Implikací do reality tedy může být zjištění, že kromě ceny jízdenky a hodnoty pokuty může mít na chování cestujících vliv i způsob, jakým je kontrola agenty vnímaná. Toto zjištění ovšem potřebuje ověření v realitě.
Kód
Zdrojový kód (*.nlogo) modelu: File:Xsvaf02 ppgwp mhd.nlogo
Reference
ANTAR. Trolejbusy v Praze: Návrat turniketů do metra: blbost ekonomická. [online]. 2012, 31. 03. 2012 [cit. 2013-05-19]. Dostupné z: http://www.trolejbusyvpraze.net/blbosti_turnikety2.htm#ztraty_spravne
CAMERER, Colin. Behavioral game theory: experiments in strategic interaction. Princeton, N.J.: Princeton University Press, c2003, xv, 550 p. ISBN 06-910-9039-4.
FROŇKOVÁ, Pavlína. Co ovlivňuje počet černých pasažérů v MHD? [online]. Praha, 2012 [cit. 2013-05-19]. Dostupné z: https://isis.vse.cz/zp/portal_zp.pl?podrobnosti=104131. Bakalářská práce. Vysoká škola ekonomická v Praze. Vedoucí práce Ing. Jiří Lahvička.
NOVÁ, Magdalena a BERNÝ, Aleš. Praha žádá vyšší pokuty pro černé pasažéry, DP váhá. IDNES.cz [online]. 2007, 15. listopadu 2007 [cit. 2013-05-19]. Dostupné z: http://zpravy.idnes.cz/praha-zada-vyssi-pokuty-pro-cerne-pasazery-dp-vaha-fwp-/domaci.aspx?c=A071115_095354_praha_itu
JAROLÍMOVÁ, Monika. Analýza černých pasažérů v pražské MHD [online]. Praha, 2012 [cit. 2013-05-19]. Dostupné z: https://isis.vse.cz/zp/portal_zp.pl?podrobnosti=57475. Bakalářská práce. Vysoká škola ekonomická v Praze. Vedoucí práce Petr Bartoň.
KRAUS, Martin a Martin KOČÍ. Průzkum počtu černých pasažérů v pražské MHD v závislosti na věku respondentů [online]. Praha, 2011 [cit. 2013-05-19]. Dostupné z: http://projekty234.websnadno.cz/kraus_koci.pdf. Semestrální práce. ČVUT.
LIDOVKY.CZ. Návrat turniketů do metra vyjde na 1,5 miliardy. www.lidovky.cz: Doprava [online]. 2011, 30. srpna 2011 [cit. 2013-05-19]. Dostupné z: http://byznys.lidovky.cz/navrat-turniketu-do-metra-vyjde-na-1-5-miliardy-fo5-/doprava.aspx?c=A110830_164306_ln-doprava_nev
LORENC, Václav. Černí pasažéři: Kdo si hraje, neplatí. Zatím!. Finmag.cz [online]. 2011, 23.03.2011 [cit. 2013-05-19]. Dostupné z: http://www.finmag.cz/cs/finmag/penize/byt-cerny-je-hra-zatim/
MARKYTÁNOVÁ, Eva. Opravdu dokážou stále vyšší pokuty v pražské MHD odradit cestující od jízdy na "černo"? [online]. Praha, 2010 [cit. 2013-05-19]. Dostupné z: https://isis.vse.cz/zp/portal_zp.pl?podrobnosti=49281. Bakalářská práce. Vysoká škola ekonomická v Praze. Vedoucí práce Ing. Marek Hudík, Ph.D.
TSEBELIS, George. The abuse of probability in political analysis: The Robinson Crusoe fallacy. The American Political Science Review, 1989, 77-91.
TVERSKY, Amos a Daniel KAHNEMAN. Availability: A heuristic for judging frequency and probability. Cognitive Psychology. 1973, vol. 5, issue 2, s. 207-232. DOI: 10.1016/0010-0285(73)90033-9. Dostupné z: http://linkinghub.elsevier.com/retrieve/pii/0010028573900339
- ↑ Markytánová (2010), str. 19
- ↑ Froňková (2012) str. 13
- ↑ Jarolímová (2012), str. 8
- ↑ Nová, Berný (2007), Praha žádá vyšší pokuty pro černé pasažéry, DP váhá
- ↑ Antar (2012), Návrat turniketů do metra: blbost ekonomická
- ↑ Kraus, Kočí (2011), str. 6
- ↑ Lorenc (2011), Černí pasažéři: Kdo si hraje, neplatí. Zatím!
- ↑ Bohužel původní zdroj se mi nepodařilo dohledat. Kriticky okomentované shrnutí studie je k dispozici na stránkách Pirátské strany, viz http://www.pirati.cz/_media/mo/deloitte-pirati.pdf.
- ↑ Lidovky.cz (2011), Návrat turniketů do metra vyjde na 1,5 miliardy
- ↑ Volně dle Camerer (2003), str. 45
- ↑ Tsebelis (1989), str. 81
- ↑ Žádný z regresních modelů nalezených na téma černých pasažérů bohužel nešlo použít, jelikož tyto modely pracovali s jinými parametry, než zde uvažuji já.
- ↑ Tversky, Kahneman (1973)
- ↑ Krásný příklad nepřesné paměti v realitě je dlouhodobé zaměřování kontrol na určitou oblast – například přestupní stanice metra.
- ↑ Vzhledem k výpočetní náročnosti modelu nebylo v mých silách provést více opakování. Model se naštěstí ustálí zpravidla do deseti kol a nevykazuje příliš mnoho odchylek při jednotlivých bězích, takže data považuji za relevantní i při takto nízkém počtu opakování.