Předmluva

K problematice redukce rozptylu není příliš velké množství českých zdrojů. Jedná se většinou o akademické práce, které citují zahraniční autory. Texty blíže se zabývající tímto tématem jsou primárně v anglickém jazyce a k vysvětlení využívají nástroje statistiky, které nemusí být čtenáři s pouhými základními znalostmi ze statistiky příliš jasné. Jelikož i já, autor tohoto textu, oplývám pouze základními znalostmi z oboru statistiky, budu se snažit v tomto učebním textu popsat metody redukce rozptylu co možná nejjednodušeji, aby si z něj čtenáři, kteří jsou na obdobné úrovni znalostí, odnesli pokud možno jakési základy, které jim pomohou lépe toto téma pochopit. Zároveň tím apeluji na zkušenější čtenáře, aby pomohli s korekcí a rozšířením tohoto textu o hlubší poznatky ze statistiky, které by navazovaly na mnou vytvořený základ.

Náhodná veličina a její rozptyl

Náhodná veličina (též náhodná či stochastická proměnná) je nějaká libovolná veličina mající číselnou hodnotu (např. 1, -150 nebo 18,6) a jednotku (kilogram, metr, litr, ...). Tuto veličinu můžeme měřit u různých objektů, v různém čase, různém místě a pomocí teorie pravděpodobnosti a matematické statistiky s ní různě pracovat. Příkladem náhodné veličiny může být počet ok při hodu kostkou, hmotnost narozených dětí v různých regionech, roční mzda občanů státu apod.^[1]

Náhodná veličina může být buď diskrétního nebo spojitého typu. Oba typy si jsou velmi podobné, což je vidět v následujících podkapitolách.

Diskrétní náhodná veličina

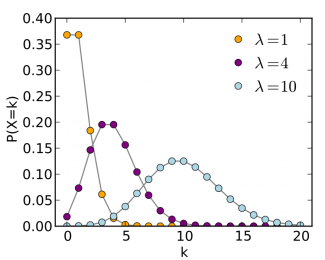
Pravděpodobnostní funkce diskrétního Poissonova rozdělení^[2].

Distribuční funkce diskrétního Poissonova rozdělení^[3].

Diskrétní (též nespojitá) náhodná veličina je taková náhodná veličina, která může nabývat pouze jednotlivých hodnot z konečného nebo nekonečného intervalu. To znanená, že se může měnit jen po skocích^[1]. Příkladem spojité náhodné veličiny může být počet ok při hodu kostkou, který může nabývat pouze hodnot Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \{ 1, 2, 3, 4, 5, 6 \}} .

Zkoumáme-li potom pravděpodobnost, že na hozené kostce padne konkrétní hodnota, můžeme těmto možným hodnotám přiřadíit jejich pravděpodobnost výskytu, čímž získáme pravděpodobnostní funkci diskrétní náhodné veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} . Sestavením tabulky s možnými hodnotami ok na kostce značených Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} a pravděpodobnostmi, že padne právě tento počet ok získáme průběh pravděpodobnostní funkce Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p(x)} , která každému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} přiřazuje jeho pravděpodobnost značenou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(x)} , což můžeme zapsat jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p(x) = P(X = x)} , slovy "pravděpodobnost, že náhodná veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} nabyde hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} ".

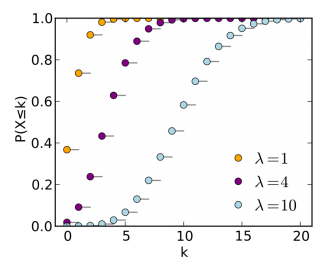
Kromě pravděpodobnostní funkce nás zajímá také distribuční funkce Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)} , a to v případech, kdy chceme určit pravděpodobnost, že veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} nabyde hodnoty menší než Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} , což lze zapsat jako

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x) = P(X < x)}

a v případě diskrétní náhodné veličiny ji lze určit "nasčítáním" všech předchozích pravděpodobností před zvolenou hodnotou, tedy touto sumací:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x) = \sum_{i=1}^{x}P(X = x_{i})} .

Známe-li hodnoty, kterých může náhodná veličina nabývat, a pravděpodobnosti výskytu těchto hodnot, můžeme spočítat střední hodnotu (též označnovanou jako první počáteční moment) jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X) = \sum_{i=1}^{x}x_{i} P(x_{i})}

Pro příklad si můžeme představit obyčejnou šestihrannou kostku. Pravděpodobnost, že padne jedna z 6 možných hodnot na kostce stejná, proto pravděpodobnostní funkci lze zapsat jako

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p(x) = \frac{1}{6}} .

A protože tyto hodnoty pokrývají všechny možné, které mohou nastat, je jejich součet roven jedné. Platí tedy vztah

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^{n}P(x_{i}) = 1} .

Díky tomu, že jsou pravděpodobnosti v tomto případě vždy stejné, zjednodušuje se tím i vzoreček pro výpočet střední hodnoty, který je potom pouze

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X) = \frac{1}{n}\sum_{i=1}^{x}x_{i}} .

Jedná se v podstatě o prostý aritmetický průměr. Kdybychom ale zkoumali náhodnou veličinu, kterou by byl součet ok na dvou hozených kostkách, nebyla by pravděpodobnost vždy stejná, protože například součet 5 můžeme hodit čtyřmi způsoby: (1,4), (2, 3) (3, 2), (4, 1), a tudíž bychom nemohli použít prostého aritmetického průměru^[4].

Spojitá náhodná veličina

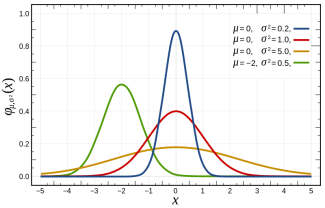
Hustota pravděpodobnosti spojitého Normálního rozdělení^[5].

Distribuční funkce spojitého Normálního rozdělení^[6].

Spojitá náhodná veličina je taková náhodná veličina, která může nabývat všech možných hodnot z konečného nebo nekonečného intervalu, může se tedy měnit bez skoků (spojitě)^[1]. Ekvivalentem diskrétní pravděpodobnostní funkce je zde hustota pravděpodobnosti značená Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} ^[4].

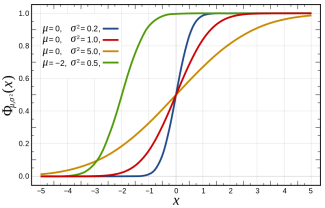
Spojitá náhodná veličina má rovněž distribuční funkci Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(X)} , kterou získáme když budeme integrovat hustotu pravděpodobnosti od mínus nekonečna do Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} : F(X)=\int_{-\infin}^{x}f(t)dt. Chceme-li naopak z distribuční funkce získat hustotu pravděpodobnosti, stačí nám provést inverzní operavi k integrálu, kterou je derivace: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)=F'(x)}

Stejně jako v případě pravděpodobnostní u diskrétní náhodné veličiny, hustota pravděpodobnosti u spojité náhodné veličiny splňuje podmínku

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty}f(x)dx=1}

Střední hodnotu pak dostaneme podobně jako u diskrétní funkce, a to integrováním hustoty pravděpodobnosti násobené hodnotou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(X)=\int_{-\infty}^{\infty}xf(x)dx}

Spojitou veličinu můžeme "převést" na diskrétní tak, že její průběh rozdělíme do dílčích intervalů^[1]. Kdybychom například zkoumali hmotnosti pro zápasy v bojových sporetch a předpokládali, že hmostnosti účastníků budou rozděleny od 60 kg výše, čemuž odpovídá interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 60, \infty ) } a chtěli bychom určit 6 váhových katerogií, rozdělili bychom původní interval například takto^[7]:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 60, 66) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 66, 73) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 73, 81) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 81, 90) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 90, 100) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \langle 100, \infty) }

Pravděpodobnostní rozdělení

Podrobnější informace o pravděpodobnostních rozděleních

Pravděpodobnostní rozdělení (též rozdělení, rozložení nebo distribuce pravděpodobnosti) je pravidlo, podle kterého je každému náhodnému jevu přiřazena určitá (známá) pravděpodobnost. Pravděpodobnostní rozdělení se v závislosti na typu náhodné veličiny dělí na diskrétní (např. Alternativní, Binomické, Nagativní binomické, Poissonovo rozdělění) a spojitá (např. Rovnoměrné, Normální, Exponenciální, Logaritmicko-normální rozdělění).

Rozptyl

Rozptyl (též střední kvadratická odchylka, variance nebo disperze) je jednou z charakteristik náhodné veličiny, konkrétně jde o charakteristiku variability a udává, jak moc jsou hodnoty v našem statistickém souboru rozptýleny^[4].

Uvažujeme-li náhodnou veličinu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} , pak její rozptyl se označuje Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2(X)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S^2(X)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D(X)} nebo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(X)} a spočítá se jako "střední hodnota kvadrátů odchylek od střední hodnoty".

Pro diskrétní náhodnou veličinu tuto větu můžeme vyjádřit vztahem

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2 = \sum_{i=1}^n {\left[x_i - \operatorname{E}(X)\right]}^2 p_i} ,

kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i} jsou hodnoty, kterých může náhodná veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} nabývat (s pravděpodobnostmi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_i} ) a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} je střední hodnota veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} . Chceme-li rozptyl počítat "ručně", je vhodnější použít tzv. výpočetní tvar^[4]

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2 = \sum_{i=1}^n x_i^2 p_i - {[\operatorname{E}(X)]}^2}

Pro spojitou náhodnou veličinu je vztah podobný, jen místo sčítání integrujeme. Vztah vypadá potom takto

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2 = \int_{-\infty}^\infty {\left[x-\operatorname{E}(X)\right]}^2 f(x)\mathrm{d}x} ,

kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)} je hustota pravděpodobnosti veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} .

A obdobně jako u diskrétní náhodné veličiny, i zde můžeme použít jednodušší "výpočetní tvar"^[4]

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2 = \int_{-\infty}^\infty x^2 f(x)\mathrm{d}x - {[\operatorname{E}(X)]}^2}

Zákon velkých čísel a centrální limitní věta

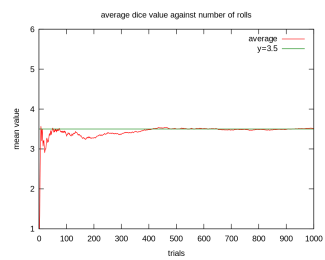
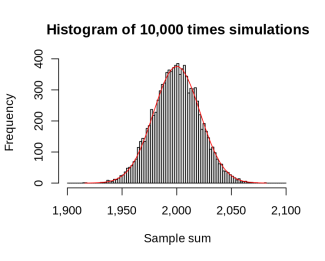
Zákon velkých čísel a konvergence výběrového průměru k teoretiské střední hodnotě při hodu šestihrannou kostkou^[8].

Centrální limitní věta a znázornění obecného diskrétního rozdělení, které se blíží rozdělení normálnímu^[9].

Při použití metody Monte Carlo v podstatě generujeme obrovské množství scénářů, které potom skládáme dohromady průměrováním. V tom nám pomáhá zákon velkých čísel a centrální limitní věta

Zákon velkých čísel lze nejlépe ilustrovat na příkladu s házením kostkou. Budeme-li házet 6hrannou kostkou stále dokola a získané hodnoty, které na kostce padly, průměrovat, tak s rostoucím počtem pokusů náš zaznamenávaný průměr bude asymptoticky kolísat kolem teoretické (vypočtené) střední hodnoty^[10]:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1+2+3+4+5+6}{6} = 3,5.}

Lze tedy říci, že výběrový průměr

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{X}_n=\frac1n(X_1+\cdots+X_n) }

bude konvergovat ke střední hodnotě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}{}\\ \overline{X}_n \, \to \, \mu \qquad\textrm{pro}\qquad n \to \infty \\{}\end{matrix}}

Díky centrální limitní větě potom můžeme využívat toho, že při velkém počtu opakování Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} bude mít libovolná veličina přibližně normální rozdělení se snižujícím se rozptylem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma^2}{n}} ^[11].

Metoda Monte Carlo

Podrobnější informace o metodě Monte Carlo

V simulacích pomocí metody Monte Carlo se snažíme pomocí generování náhodných čísel a mnoha opakování náhodných pokusů získat obecné charakteristiky nějakého modelovaného jevu. To je možné díky platnosti zákona velkých čísel a centrální limitní věty. Pomocí metody Monte Carlo lze získávat relativně jednoduše přibližné výsledky tam, kde by bylo použití analytických modelů složité, ba nemožné. Metody Monte Carlo je využíváno i například v systémech založených na teorii front.

Metody redukce roptylu

Když provádíme simulaci, obvykle v rámci nějaké studie, zajímá nás jedna nebo více sledovaných hodnot nějakého stochastického (nedeterministického) modelu. Například chceme zjistit, dlouhodobou střední (průměrnou) dobu čekání zákazníků ve frontě, kterou budeme značit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W}} . Střední dobu čekání značme například Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(W)} . Abychom odhadli Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(W)} , musíme provést Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{K}} nezávislých simulací. Po provedení těchto simulací a zjištění středních hodnot dob čekání Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(W_i)} lze stanovit estimátor Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(W)} podle vztahu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\overline{W}} = \frac{\sum_{i=1}^K W_i}{K}} . Kdybychom však našli jiný nezkreslený estimátor střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(W)} s menším rozptylem než má Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\overline{W}}} , získali bychom tím estimátor s menším intervalem spolehlivosti, což je pro náš žádoucí. Pro zredukování rozptylu estimátoru Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\overline{W}}} lze použít několik metod, které jsou popsány v následujících kapitolách. I ty jednodšší podávají vcelku dobré výsledky. Je ale třeba dát si pozor, protože nesprávným použitím některých metod může místo snížení rozptylu naopak dojít k jeho zvýšení^[12].

Metoda společných náhodných čísel

Metoda společných náhodných čísel využívá toho, že pokud zkoumáme a porovnáváme dva různé systémy, které obsahují nějaké náhodně se chovající komponenty, je obecně lepší při vyhodnocování takovýchto systémů v nich používat vždy stejně implementované náhodné komponenty. Metoda využívá klíčové vlastnosti dvou náhodných veličin Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} , která je dána vztahem

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(X-Y) = \operatorname{var}(X) + \operatorname{var}(Y) - 2\operatorname{cov}(X,Y)} .

Jestliže jsou náhodné veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} závislé a jsou pozitivně korelovány, tzn. že platí i Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{cov}(X,Y) > 0} , potom bude rozptyl rozdílu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X-Y}} menší než kdyby veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} byly nezávislé. Obecně použití metody společných náhodných čísel vede k tomu, že i výsledky simulace dvou takto zkoumaných systémů budou pozitivně korelovány, proto je při porovnávání dvou systémů lepší použít společná náhodná čísla místo zcela nezávislých náhodných čísel.

Problém by nastal, pokud by byly veličiny negativně korelovány. V takovém případě by došlo naopak ke zvýšení rozptylu, což je ve většině případů nežádoucí^[12].

Příklad užití metody společných náhodných čísel

Pro ilustraci metody společných náhodných čísel použijeme následující příklad zabývající se zpracováním konečného počtu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N}} úkolů, které jsou zpracovávány dvěma identickými stroji. Doby zpracování úkolů na jednotlivých strojích jsou náhodné veličiny z nějakého obecného rozdělení, jehož distribuční funkci označmě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{F}} . Naším úkolem je porovnat čas dokončení posledního úkolu, značený Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{C_{max}}} , za platnosti dvou různých pravidel. Prvním pravidlem je LPTF (Longest Processing Time First), podle něhož si stroj bude vybírat z množiny ještě nezpracovaných úkolů ty úkoly, jejichž doba zpracování je největší. Druhé zkoumané pravidlo SPTF (Shortest Processing Time First) bude stroji říkat, aby si z množiny zbývajících úkolů vybíral nejprve ty nejkratší, čili ty s nejmenší dobou zpracování^[12].

Srovnáme-li výsledky simulace pro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N} = 10} úkolů s délkou z exponenciálního rozdělení s distribuční funkcí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{F} = 1 - e^{-x}} , pak dostaneme jiné estimátory a intervaly spolehlivosti pro střední hodnotu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{SPTF}-C_{max}^{LPTF}})} , když použijeme společná náhodná čísla, než když je nepoužijeme. Srovnání sledovaných hodnot znázorňují následující dvě tabulky, z nichž první ukazuje hodnoty získané bez použití metody nezávislých náhodných čísel, a druhá ukazuje snížení rozptylu právě použitím této metody^[12].

Tabulka 3: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{SPTF}-C_{max}^{LPTF}})} bez použití této metody^[12]
Počet běhů simulace	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8138}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,5745}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,645; 0,973)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8293}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,4976}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,780; 0,878)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 100 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8487}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,4990}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,833; 0,864)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8398}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2,4951}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,835; 0,845)}

Tabulka 4: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{SPTF}-C_{max}^{LPTF}})} s použitím metody společných náhodných čísel^[12]
Počet běhů simulace	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8559}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,5416}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,822; 0,889)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8415}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,5230}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,831; 0,852)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 100 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8394}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,5164}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,836; 0,843)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,8391}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,5168}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,838; 0,840)}

Z hodnot je patrné, že došlo přibližně k 5násobnému snížení směrodatné odcyhlky, a tím i k 5násobnému zúžení intervalu spolehlivosti.

Při použití této metody však existuje riziko vyplývající s nutnosti použití stejných náhodných počátečních čísel při generování náhodných veličin v obou systémech. Tento problém se synchronizací by mohl nastat, kdybychom uvažovali systém front Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G/G/1}} , v němž může server pracovat dvěma různými rychlostmi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{v_1}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{v_2}} . Kdybychom v tomto případě chtěli získat estimátor pro rozdíl v čekacích dobách za použití různých rychlostí, museli bychom v rámci této metody použít stejné mezičasy zpracování a stejně velké požadavky. (Dobu obsluhy bychom získali podílem velikosti požadavku a rychlosti serveru.) Tím bychom narazili na problém synchroznizace, protože při vyšší rychlosti zpracování úkolů by se fronta posouvala rychleji^[12]. Tento problém lze vyřešit dvěma způsoby:

Použitím více oddělených toků náhodných čísel pro různé sekvence náhodných veličin potřebných k provedení simulace.
Zajištěním, že budou náhodné veličiny generovány v přesně stejném pořadí v obou zkoumaných systémech.

Pozn.: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G/G/1}} fronta představuje délku fronty v systému s Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{1}} jediným serverem, kde mají mezičasy nějaké obecné rozdělení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G}} (jako General - obecné) a časy obsluhy jiné obecné rozdělení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G}} ^[13]

Antitetické proměnné

Metoda antitetických proměnných využívá skutečnosti, že pokud je náhodná veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U}} z rozvnoměrného rozdělení nabývajícího hodnot z intervalu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0, 1)} , pak musí platit, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 - \operatorname{U}} je také z rovnoměrného rozdělení. Zároveň využívá toho, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 - \operatorname{U}} musí být nutně negativně korelované (když se zvýší Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U}} , logicky musí dojít ke snížení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 - \operatorname{U}} a naopak)^[12].

Klíčovou myšlenkou celé této metody je pak to, že máme-li dva výsledky po sobě jdoucích simulací Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_1}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_2}} , pak platí, že

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(\frac{W_1 + W_2}{2}) = \frac{1}{4}\operatorname{var}(W_1) + \frac{1}{4}var(W_2) + \frac{1}{2}\operatorname{cov}(W_1, W_2)}

Z tohoto vztahu vyplývá, že budou-li výsledky simulace Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_1}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_2}} negativně korelovány, bude jejich rozptyl Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(\frac{W_1 + W_2}{2})} menší, než kdyby na sobě oba výsledky nebyly závislé.

Otázkou je, jak zajistíme, aby výsledky dvou po sobě jdoucích běhů simulace byly negativně korelované. Jak už bylo zmíněno dříve, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 - \operatorname{U}} jsou negativně korelované, díky čemuž můžeme předpokládat, že když pro první běh simulace použijeme náhodné proměnné Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U_1,...,U_m}} k výpočtu výsledku simulace Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_1}} a poté použijeme použijeme náhodné proměnné Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{1 - U_1,...,1 - U_m}} k výpočtu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_2}} , bude to znamenat, že i Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_1}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{W_2}} budou negativně korelované. Selský rozum nám říká, že v obdobném případě se simulací fronty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G/G/1}} povede velké množství hodnot z Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{U_i}} , kterým odpovídají dlouhé časy obsluhy, k dlouhým čekacím dobám v prvním běhu simulace. Použití antitetických proměnných Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{1 - U_i}} v druhém běhu simulace způsobí naopak krátké časy obsluhy, a tím i krátké čekací doby^[12].

Příklad užití metody antitetických proměnných

Výsledky použití antitetických proměnných znázorňují následujícíc dvě tabulky, z nichž první ukazuje odhad střední doby trvání posledního úkolu bez použití této metody a druhá s použitím této metody.

Tabulka 5: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{LPTF}})} bez použití této metody^[12]
Počet běhů simulace	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0457}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1,6201}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (4,945; 5,146)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0400}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1,6020}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,009; 5,071)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 100 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0487}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1,597}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,039; 5,059)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1 000 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0559}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1,5980}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,053; 5,059)}

Tabulka 6: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{LPTF}})} s použitím metody antitetických proměnných^[12]
Počet párů proměnných	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 500}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0711}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,7216}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,008; 5,134)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0497}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,6916}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,030; 5,069)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 50 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0546}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,6858}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,049; 5,061)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 500 000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 5,0546}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0,6844}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (5,053; 5,056)}

Srovnáme-li opět výsledky simulace pro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N} = 10} úkolů s délkou z exponenciálního rozdělení s distribuční funkcí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{F} = 1 - e^{-x}} , pak dostaneme jiné estimátory a intervaly spolehlivosti pro střední hodnotu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{C_{max}^{LPTF}})} , když použijeme metodu antitetických proměnných, než když je nepoužijeme. Srovnáváme zde výsledky 1000 nezávislých běhů simulace s 1000 záviclých běhů sestávajích z 500 dvojic běhů, které jsou na vzájemně závislé a používají právě antitetické proměnné. Z hodnot tabulky je patrné, že došlo k 1,5násobnému snížení směrodatné odchylky, a tím i k 1,5násobnému zúžení intervalů spolehlivosti^[12].

Je nutno podotknout, že podobně jako při použití metody společných náhodných čísel, i zde může dojít k problému se synchronizací. Dále je užitečné uvést, že tato metoda je určitě jednodušší na implementaci, protože nám stačí pouze jeden zdroj rovnoměrně rozložených náhodných čísel k vygenerování jendoho páru antitetických proměnných.

Metoda řídících proměnných

Metoda řídících proměnných je založena na myšlence, která říká, že pokud chceme odhadnout střední hodnotu neznámé veličiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} měřící výkonnost za použití Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{K}} nezávislých běhů simulace, pak pro výstup i-tého běhu simulace Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X_i}} bude platit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X_i) = \operatorname{E}(X)} . Nezkreslený estimátor pro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} je dán jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\overline{X}) = \frac{(\sum_{i=1}^K X_i)}{K}} . Navíc předpokládejme, že jsme zároveň schopni simulovat průběh související výstupní proměnné Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y_i}} , pro kterou platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(Y_i) = \operatorname{E}(y)} a my Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(Y)} už známe. Označíme-li nezkreslený estimátor Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(Y)} jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\overline{Y}) = \frac{(\sum_{i=1}^K Y_i)}{K}} , pak pro libovolnou konstantu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{c}} je součet Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{X} + c(\overline{Y}-E(Y))} také nezkresleným estimátorem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} . Z následujícího vztahu

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(\overline{X}+c(\overline-E(Y))) = \operatorname{var}(\overline{X}) + c^2\operatorname{var}(\overline{Y}) + 2c\operatorname{cov}(\overline{X},\overline{Y})}

lze vyvodit, že rozptyl Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(\overline{X} + c(\overline{Y}-E(Y)))} bude minimalizován, pokud použijeme konstantu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{c} = \operatorname{c*}} , kde

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{c*} = -\frac{\operatorname{cov}(\overline{X},\overline{Y})}{\operatorname{var}(\overline{Y})}} ^[12].

Bohužel, konkrétní hodnoty pro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{cov}(\overline{X},\overline{Y})} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(\overline{Y})} obvykle neznáme předem, musíme je ohdadnout ze simulovaných dat. Hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{Y}} se zde nazývá řídící proměnná estimátoru Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{X}} .

Tato metoda funguje díky tomu, že uvažujeme-li pozitivně korelované Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{X}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{Y}} , pak v simulaci, kde je hodnota výstupu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{Y}} mnohem vyšší než průměrná hodnota výstupu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\overline{Y})} , bude pravděpodobné, že i vstupní hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{X}} bude větší než její průměr Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\overline{X})} , což můžeme opravit tak, že snížíme hodnotu vstupní proměnné (estimátoru) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\overline{X})} . Totéž platí analogicky i pro negativně korelované proměnné^[12].

V příkladě s produkční linkou by jako přirozeně vzniklá řídící proměnná mohla být dlouhodobá průměrná rychlost produkce linky, která má nárazníky (buffery) o nulové délce.

Metoda závislých proměnných

Tato metoda je založena na následujících dvou vztazích. Jestliže Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} jsou dvě libovolné náhodné veličiny, pak platí

1. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X) = \operatorname{E}(\operatorname{E}(X|Y))}

2. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{var}(X) = \operatorname{E}(\operatorname{var}(X|Y)) + \operatorname{var}(\operatorname{E}(X|Y)) >= \operatorname{var}(\operatorname{E}(X|Y))} ,

z čehož vyplnývá, že náhodná veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X|Y)} bude mít stejnou střední hodnotu jako náhodná veličina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} , a navíc bude mít menší rozptyl než Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} ^[12].

Tyto vztahy nám mohou pomoci snížit rozptyl v simulacích. Předpokládejme, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} bude nějaký výkonnostní ukazatel, který chceme odhadnout. Jestliže zavedeme náhodnou proměnnou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} takovou, že budeme znát Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X|Y = y)} , tak z předchozích dvou vztahů můžeme předpokládat, že pro nás bude lepší simulovat Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y}} a tedy používat Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X|Y)} , než přímo simulovat veličinu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} .

Ukažme si to na příkladu modelu fronty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M_{\lambda}/M_{\mu}/1/N} , ve kterém systém nepřijme více než Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N}} zákazníků, ti budou ze systému ztraceni. Cílovou veličinou, kterou budeme sledovat, je střední doba ztracených zákazníků Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} v daném čase Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{t}} . Kdybychom pracovali přímo s veličinou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X}} , tak bychom provedli Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{K}} simulací až do okamžiku Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{t}} . Počet ztracených zákazníků v jednotlivých simulacích značme Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{X_i}} . Nezkreslený estimátor Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} by potom byl Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\overline{X}} = \frac{\sum_{i=1}^K X_i}{K}} .

Díky použití této metody ale můžeme rozptyl estimátoru snížit následovně. Uvažujme nejprve Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{Y_i}} , které bude značit celkový čas z intervalu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,\operatorname{t})} , při počtu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N}} zákazníků v systému v i-tém běhu simulace. Díky tomu, že příchody zákazníků jsou z Poissonova rozdělení s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\lambda}} , pak naše podmíněná střední hodnota bude Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X|Y_i) = \lambda Y_i} . Změní se tím i estimátor, který bude nyní Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda \overline{Y}} , kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\overline{Y}} = \frac{\sum_{i=1}^K Y_i}{K}} .

Následující tabulky srovnávají hodnoty estimátoru Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(X)} a intervaly spolehlivosti pro různé počty simulací s parametry Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\lambda} = 0,5} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{\mu} = 1} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{N} = 3} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{t} = 1000} získané bez použití metody závislých proměnných, a druhá ukazuje snížení rozptylu právě použitím této metody^[12].

Tabulka 5: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{X})} bez použití této metody^[12]
Počet běhů simulace	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,10}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10,06}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (26,86; 39,33)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 100}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,09}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 9,21}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (32,28; 35,90)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,60}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 8,88}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (33,05; 34,15)}

Tabulka 6: Odhad střední hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{E}(\operatorname{X})} s použitím metody podmíněných proměnných^[12]
Počet běhů simulace	Střední hodnota	Směrodatná odchylka	95% interval spolehlivosti
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,60}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 7,16}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (29,17; 38,05)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 100}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,82}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 6,91}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (32,46; 35,18)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1000}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 33,36}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 6,57}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (32,95; 33,76)}

Z hodnot v tabulce je patrné, že metoda podmíněných proměnných snížila směrodatnou odchylku 1,3krát, čímž i zúžila interval spolehlivosti 1,3krát.

Další metody pro redukci rozptylu

Kromě již uvedených metod snižování rozptylu existují ještě další, které stojí za zmínku a jsou v praxi používány. Mezi ty patří^[14]:

Metoda momentů
Výběr podle důležitosti
Stratifikovaný výběr
Regresní modely

Závěr

Díky uvedeným metodám lze snížit rozptyl v simulacích, které využívají metodu Monte Carlo. Některé metody pomohou snížit rozptyl více, některé méně, přičemž z uvedených metod dokázala nejvíce snížit rozptyl metoda Antitetických proměnných. V závislosti na typu úlohy a nám známých informacích bychom neměli volit zbytečně složitou metodu. Při snaze o snižování rozptylu je nutné mít na paměti, že ne vždy je čas strávený nad imlementací některé z metod kompenzován odpovídajícím výsedkem. V praxi se totiž může stát, že námi navržený model bude obsahovat nedostatky, které se projeví negativně na kvalitě výsledku mnohonásobně více než vyšší rozptyl.

Zdroje

↑ ^1.0 ^1.1 ^1.2 ^1.3 Náhodná veličina Veterinární a farmaceutická univerzita Brno [online]. [cit. 2016-06-08]. Dostupné z: http://cit.vfu.cz/statpotr/POTR/Teorie/Predn1/nahvelic.htm
↑ Pravděpodobnostní funkce diskrétního Poissonova rozdělení Skbkekas 2010-02-10 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Poisson_pmf.svg
↑ Distribuční funkce diskrétního Poissonova rozdělení Skbkekas 2010-02-10 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Poisson_cdf.svg
↑ ^4.0 ^4.1 ^4.2 ^4.3 ^4.4 NÁHODNÁ VELIČINA Vysoká škola báňská - Technická univerzita Ostrava - VŠB-TUO [online]. [cit. 2016-06-08]. Dostupné z: hhttps://homen.vsb.cz/~oti73/cdpast1/KAP03/PRAV3.HTM
↑ Hustota pravděpodobnosti spojitého Normálního rozdělení Inductiveload 2008-04-02 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Normal_Distribution_PDF.svg
↑ Distribuční funkce spojitého Normálního rozdělení Inductiveload 2008-04-02 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Normal_Distribution_PDF.svg
↑ Rozdělení závodníků podle věku a hmotnosti AC Sparta Praha Judo [online]. [cit. 2016-06-05]. Dostupné z: http://www.sparta-judo.cz/judo-jako-sport/vekove-a-vahove-kategorie/
↑ Zákon velkých čísel - hody kostkou NYKevin 2010-01-31 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Largenumbers.svg
↑ Podobnost rozdělení - Centrální limitní věta Chen-Pan Liao 2014-11-15 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Central_theorem_2.svg
↑ Law of large numbers encyclopediaofmath.org [online]. [cit. 2016-06-05]. Dostupné z: https://www.encyclopediaofmath.org/index.php/Law_of_large_numbers
↑ Central Limit Theorem Robert D. Klauber 2015-06-07 [online]. [cit. 2016-06-09]. Dostupné z: http://www.quantumfieldtheory.info/CentralLimitTheorem.pdf
↑ ^12.00 ^12.01 ^12.02 ^12.03 ^12.04 ^12.05 ^12.06 ^12.07 ^12.08 ^12.09 ^12.10 ^12.11 ^12.12 ^12.13 ^12.14 ^12.15 ^12.16 ^12.17 Variance Reduction Techniques Technische Universiteit Eindhoven University of Technology [online]. [cit. 2016-06-07]. Dostupné z: http://www.win.tue.nl/~resing/2S540/week6.pdf
↑ Wiley Encyclopedia of Operations Research and Management Science S. Foss 2001 [cit. 2016-06-09]. ISBN: 9780470400531
↑ Simulační metody při hodnocení cenných papírů Mgr. Michal Tvrdík 2007-09-20 [online]. [cit. 2016-06-05]. Dostupné z: https://is.cuni.cz/webapps/zzp/detail/46348/

[nahv-1] 1.0 ^1.1 ^1.2 ^1.3 Náhodná veličina Veterinární a farmaceutická univerzita Brno [online]. [cit. 2016-06-08]. Dostupné z: http://cit.vfu.cz/statpotr/POTR/Teorie/Predn1/nahvelic.htm

[poiss1-2] Pravděpodobnostní funkce diskrétního Poissonova rozdělení Skbkekas 2010-02-10 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Poisson_pmf.svg

[poiss2-3] Distribuční funkce diskrétního Poissonova rozdělení Skbkekas 2010-02-10 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Poisson_cdf.svg

[ban-4] 4.0 ^4.1 ^4.2 ^4.3 ^4.4 NÁHODNÁ VELIČINA Vysoká škola báňská - Technická univerzita Ostrava - VŠB-TUO [online]. [cit. 2016-06-08]. Dostupné z: hhttps://homen.vsb.cz/~oti73/cdpast1/KAP03/PRAV3.HTM

[norm1-5] Hustota pravděpodobnosti spojitého Normálního rozdělení Inductiveload 2008-04-02 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Normal_Distribution_PDF.svg

[norm2-6] Distribuční funkce spojitého Normálního rozdělení Inductiveload 2008-04-02 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Normal_Distribution_PDF.svg

[judo-7] Rozdělení závodníků podle věku a hmotnosti AC Sparta Praha Judo [online]. [cit. 2016-06-05]. Dostupné z: http://www.sparta-judo.cz/judo-jako-sport/vekove-a-vahove-kategorie/

[llno-8] Zákon velkých čísel - hody kostkou NYKevin 2010-01-31 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Largenumbers.svg

[clto-9] Podobnost rozdělení - Centrální limitní věta Chen-Pan Liao 2014-11-15 [online]. [cit. 2016-06-08]. Dostupné z: https://commons.wikimedia.org/wiki/File:Central_theorem_2.svg

[lln-10] Law of large numbers encyclopediaofmath.org [online]. [cit. 2016-06-05]. Dostupné z: https://www.encyclopediaofmath.org/index.php/Law_of_large_numbers

[clt-11] Central Limit Theorem Robert D. Klauber 2015-06-07 [online]. [cit. 2016-06-09]. Dostupné z: http://www.quantumfieldtheory.info/CentralLimitTheorem.pdf

[vrt-12] 12.00 ^12.01 ^12.02 ^12.03 ^12.04 ^12.05 ^12.06 ^12.07 ^12.08 ^12.09 ^12.10 ^12.11 ^12.12 ^12.13 ^12.14 ^12.15 ^12.16 ^12.17 Variance Reduction Techniques Technische Universiteit Eindhoven University of Technology [online]. [cit. 2016-06-07]. Dostupné z: http://www.win.tue.nl/~resing/2S540/week6.pdf

[foss-13] Wiley Encyclopedia of Operations Research and Management Science S. Foss 2001 [cit. 2016-06-09]. ISBN: 9780470400531

[tvrdik-14] Simulační metody při hodnocení cenných papírů Mgr. Michal Tvrdík 2007-09-20 [online]. [cit. 2016-06-05]. Dostupné z: https://is.cuni.cz/webapps/zzp/detail/46348/

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

Metody redukce rozptylu

Contents

Předmluva

Náhodná veličina a její rozptyl

Diskrétní náhodná veličina

Spojitá náhodná veličina

Pravděpodobnostní rozdělení

Rozptyl

Zákon velkých čísel a centrální limitní věta

Metoda Monte Carlo

Metody redukce roptylu

Metoda společných náhodných čísel

Příklad užití metody společných náhodných čísel

Antitetické proměnné

Příklad užití metody antitetických proměnných

Metoda řídících proměnných

Metoda závislých proměnných

Další metody pro redukci rozptylu

Závěr

Zdroje

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

Contents

Tools

In other languages