Difference between revisions of "Vickrey auction/cs"
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{DISPLAYTITLE:Vickreyova aukce}} | ||
==Úvod== | ==Úvod== | ||
| − | Tento učební text se zabývá jedním specifickým typem aukce, kterým je aukce Vickreyova. Nejprve jsou popsány její charakteristiky, poté historie vzniku, dále je vysvětlen strategický postup při této aukci a nakonec je uvedeno několik příkladů, ať již těch jednodušších pro pochopení principu fungování, tak těch složitějších. Jsou také zmíněny případy, kdy se tento typ aukce používá v praxi, kterých překvapivě není málo. | + | Tento učební text se zabývá jedním specifickým typem aukce, kterým je aukce <b>Vickreyova</b>. Nejprve jsou popsány její charakteristiky, poté historie vzniku, dále je vysvětlen strategický postup při této aukci a nakonec je uvedeno několik příkladů, ať již těch jednodušších pro pochopení principu fungování, tak těch složitějších. Jsou také zmíněny případy, kdy se tento typ aukce používá v praxi, kterých překvapivě není málo. |
==Základní charakteristiky== | ==Základní charakteristiky== | ||
| − | Tomu, kdo se o aukce nijak více nezajímá, může následující popis připadat zbytečně složitý nebo na první pohled poněkud nesmyslný. Jak se ale v dalších odstavcích ukáže, vše má svůj smysl. Vickreyova aukce, častěji spíše nazývána aukcí druhé nejlepší nabídky, je jednokolová aukce probíhající obálkovou metodou, nabídky dražitelů jsou tak utajené. Nikdo tedy neví, jak si dražené položky cení ostatní účastníci. Druhým zásadním specifikem je, že ten, kdo nabídl částku nejvyšší, je sice vítěz, ale zaplatí ve skutečnosti pouze druhou nejvyšší nabízenou částku. Zpravidla se při této aukci draží jediný předmět. Ačkoli to nemusí být na první pohled jasné, tento typ aukce představuje unikátní přínosy. Jedním z nich je například rychlost, se kterou aukce probíhá. Dochází zde také k optimální alokaci zdrojů a to z toho důvodu, že dominantní strategií hráčů je nabídnutí skutečné hodnoty předmětu, resp. takové hodnoty, kterou pro daného hráče představuje.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref><ref name="Vickrey Auctions in Practice">LUCKING-REILEY, David. Vickrey Auctions in Practice: From Nineteenth-Century Philately to Twenty-First-Century E-Commerce. Journal of Economic Perspectives [online]. 2000, 14(3), 183-192 [cit. 2020-05-29]. DOI: 10.1257/jep.14.3.183. ISSN 0895-3309. Dostupné z: http://pubs.aeaweb.org/doi/10.1257/jep.14.3.183</ref> | + | Tomu, kdo se o aukce nijak více nezajímá, může následující popis připadat zbytečně složitý nebo na první pohled poněkud nesmyslný. Jak se ale v dalších odstavcích ukáže, vše má svůj smysl. Vickreyova aukce, častěji spíše nazývána <b>aukcí druhé nejlepší nabídky</b>, je <b>jednokolová</b> aukce probíhající <b>obálkovou metodou</b>, nabídky dražitelů jsou tak utajené. Nikdo tedy neví, jak si dražené položky cení ostatní účastníci. Druhým zásadním specifikem je, že ten, kdo nabídl částku nejvyšší, je sice vítěz, ale zaplatí ve skutečnosti pouze druhou nejvyšší nabízenou částku. Zpravidla se při této aukci draží jediný předmět. Ačkoli to nemusí být na první pohled jasné, tento typ aukce představuje unikátní přínosy. Jedním z nich je například rychlost, se kterou aukce probíhá. Dochází zde také k optimální alokaci zdrojů a to z toho důvodu, že dominantní strategií hráčů je nabídnutí skutečné hodnoty předmětu, resp. takové hodnoty, kterou pro daného hráče představuje.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref><ref name="Vickrey Auctions in Practice">LUCKING-REILEY, David. Vickrey Auctions in Practice: From Nineteenth-Century Philately to Twenty-First-Century E-Commerce. Journal of Economic Perspectives [online]. 2000, 14(3), 183-192 [cit. 2020-05-29]. DOI: 10.1257/jep.14.3.183. ISSN 0895-3309. Dostupné z: http://pubs.aeaweb.org/doi/10.1257/jep.14.3.183</ref> |
==Historie== | ==Historie== | ||
| Line 9: | Line 10: | ||
==Vlastnosti aukce a strategie dražitelů== | ==Vlastnosti aukce a strategie dražitelů== | ||
| − | Vickreyova aukce má z hlediska teorie her spoustu zajímavých vlastností. Zvláště zajímavá je jedna vlastnost, díky které jsou účastníci vybízení k tomu, aby postupovali čestně. Ve skutečnosti nejlepší strategií pro dražitele je právě nabídnout svou „subjektivní“ skutečnou vnitřní hodnotu, kterou pro ně daná položka představuje, resp. nakolik si jí cení.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> Obrázky spolu s jejich popisem napomáhají vysvětlit, proč je ve Vickreyově aukci nejlepší strategií čestnost a proč nemusí účastníci brát ohled na ostatní. Pro demonstrační účely byl vybrán jeden účastník aukce jménem Sam. | + | Vickreyova aukce má z hlediska teorie her spoustu zajímavých vlastností. Zvláště zajímavá je jedna vlastnost, díky které jsou <b>účastníci vybízení k tomu, aby postupovali čestně</b>. Ve skutečnosti nejlepší strategií pro dražitele je právě nabídnout svou „subjektivní“ skutečnou vnitřní hodnotu, kterou pro ně daná položka představuje, resp. nakolik si jí cení.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> Obrázky spolu s jejich popisem napomáhají vysvětlit, proč je ve Vickreyově aukci <b>nejlepší strategií čestnost</b> a proč nemusí účastníci brát ohled na ostatní. Pro demonstrační účely byl vybrán jeden účastník aukce jménem Sam. |
| − | [[File: | + | [[File:Sam_Winner_Bids_2.png|thumb|right|Vickreyova aukce - výherce Sam a jeho možné strategie|1050px]] |
| − | Obrázek vpravo zachycuje Sama ve výchozí situaci jakožto výherce aukce. Zleva první situace ukazuje stav, který je pro Vickreyovu aukci typický. Reflektuje také onu dominantní strategii – účastníci nabízejí tolik, nakolik si dané položky skutečně cení. V této situaci Sam vyhraje aukci, jeho užitek je navíc reprezentován rozdílem dvou nabídek, protože výherce Sam uhradí tu druhou. Následující situace ukazuje, že pokud Sam zvýší svou nabídku, nic se pro něj nezmění – aukci stále vyhraje on a cena, kterou musí zaplatit, zůstane stejná. Navíc se zde vystavuje riziku, že při vyšších nabídkách ostatních účastníků zaplatí více, než si dané položky cení on sám. Zleva třetí situace ukazuje, že ani snižování jeho nabídky by nemělo žádný vliv na výsledek, pokud by ovšem snížení nevedlo až do poslední situace. Zde už Sam není výhercem aukce, jeho nabídka pouze určuje částku, kterou má výherce uhradit. Samův užitek je v tomto případě nulový. Ve všech předchozích případech byl kladný.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> | + | <b>Obrázek vpravo</b> zachycuje Sama ve výchozí situaci jakožto výherce aukce. Zleva první situace ukazuje stav, který je pro Vickreyovu aukci typický. Reflektuje také onu dominantní strategii – účastníci nabízejí tolik, nakolik si dané položky skutečně cení. V této situaci Sam vyhraje aukci, jeho užitek je navíc reprezentován rozdílem dvou nabídek, protože výherce Sam uhradí tu druhou. Následující situace ukazuje, že pokud Sam zvýší svou nabídku, nic se pro něj nezmění – aukci stále vyhraje on a cena, kterou musí zaplatit, zůstane stejná. Navíc se zde vystavuje riziku, že při vyšších nabídkách ostatních účastníků zaplatí více, než si dané položky cení on sám. Zleva třetí situace ukazuje, že ani snižování jeho nabídky by nemělo žádný vliv na výsledek, pokud by ovšem snížení nevedlo až do poslední situace. Zde už Sam není výhercem aukce, jeho nabídka pouze určuje částku, kterou má výherce uhradit. Samův užitek je v tomto případě nulový. Ve všech předchozích případech byl kladný.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> |
| − | [[File: | + | [[File:Sam_Loser_Bids_2.png|thumb|right|Vickreyova aukce - v pořadí 2. Sam a jeho možné strategie|1050px]] |
| − | Na dalším obrázku Sam jako druhý v pořadí prohrává aukci. Zleva první situace ukazuje tento výchozí stav. Další dvě situace ukazují, že snižování ani zvyšování nabídky nemá na výsledek vliv. Pokud ale Sam bude jednat neupřímně a zvýší svou nabídku tak, že vyhraje a zaplatí druhou nejvyšší částku, bude muset tak uhradit více, než je jeho skutečná vnitřní hodnota, resp. nakolik ohodnotil položku on sám. | + | <b>Na dalším obrázku</b> Sam jako druhý v pořadí prohrává aukci. Zleva první situace ukazuje tento výchozí stav. Další dvě situace ukazují, že snižování ani zvyšování nabídky nemá na výsledek vliv. Pokud ale Sam bude jednat neupřímně a zvýší svou nabídku tak, že vyhraje a zaplatí druhou nejvyšší částku, bude muset tak uhradit více, než je jeho skutečná vnitřní hodnota, resp. nakolik ohodnotil položku on sám. |
Pomocí těchto situací je dokázáno, že nejlepší nabídkou je ta, která odráží skutečnou vnitřní hodnotu pro daného účastníka. Pokud se bude nabídka lišit od skutečné vnitřní hodnoty, nebude to mít žádný vliv nebo bude muset účastník zaplatit více, než pro něj daná položka představuje. Z toho vyplývá, že stanovení nabídky ve výši představující vnitřní skutečnou hodnotu, je dominantní strategií. Za povšimnutí stojí, že během dokazování nedošlo k popisu žádného vztahu mezi nabídkami ostatních účastníků nebo jejich vlastních ohodnocení.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> Díky těmto vlastnostem je Vickreyova aukce tzv. „odolná vůči strategiím“ nebo prostě a jednoduše „pravdivá“. Proto při Vickreyově aukci představuje upřímnost nejlepší strategii. Navíc v případě, kdy ostatní dražitelé nepostupují čestně, je tato dominantní strategie upřímnosti ještě výhodnější.<ref name="Algoritmy4Life">CHRISTIAN, Brian a Tom GRIFFITHS. <i>Algoritmy pro život: jak využít počítačové algoritmy při každodenním rozhodování.</i> Přeložil Filip DRLÍK. Brno : Jan Melvil Publishing, 2017. Pod povrchem. ISBN 978-80-7555-037-8.</ref> | Pomocí těchto situací je dokázáno, že nejlepší nabídkou je ta, která odráží skutečnou vnitřní hodnotu pro daného účastníka. Pokud se bude nabídka lišit od skutečné vnitřní hodnoty, nebude to mít žádný vliv nebo bude muset účastník zaplatit více, než pro něj daná položka představuje. Z toho vyplývá, že stanovení nabídky ve výši představující vnitřní skutečnou hodnotu, je dominantní strategií. Za povšimnutí stojí, že během dokazování nedošlo k popisu žádného vztahu mezi nabídkami ostatních účastníků nebo jejich vlastních ohodnocení.<ref name="GameTheoryOnline">JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. <i>Game Theory Online</i> [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/</ref> Díky těmto vlastnostem je Vickreyova aukce tzv. „odolná vůči strategiím“ nebo prostě a jednoduše „pravdivá“. Proto při Vickreyově aukci představuje upřímnost nejlepší strategii. Navíc v případě, kdy ostatní dražitelé nepostupují čestně, je tato dominantní strategie upřímnosti ještě výhodnější.<ref name="Algoritmy4Life">CHRISTIAN, Brian a Tom GRIFFITHS. <i>Algoritmy pro život: jak využít počítačové algoritmy při každodenním rozhodování.</i> Přeložil Filip DRLÍK. Brno : Jan Melvil Publishing, 2017. Pod povrchem. ISBN 978-80-7555-037-8.</ref> | ||
| − | Jedná se tak svým způsobem o aukci, kde dražitelé nabízejí za položku tolik, na kolik si ji opravdu váží a jakou pro ně má hodnotu. Zajímavý je také vztah s aukcí první nejvyšší vítězné nabídky. U této aukce posouvají účastníci své nabídky směrem dolů, aby se vyhnuli přeplacení. U Vickreyovy aukce tomu tak ale není potřeba – aukce sama nabídky optimálně upraví a to výrazně rychleji. Podle principu teorie her „rovnost výnosů“ se postupem času průměrná očekávaná prodejní cena v aukci s první nejvyšší vítěznou nabídkou přiblíží stejné hodnotě jako v případě aukce Vickreyovy. Tentýž účastník tak vyhraje položku za stejnou cenu, ale navíc bez taktizování kohokoli z účastníků. Tato aukce je i díky tomuto důvodu jedinečná.<ref name="Algoritmy4Life">CHRISTIAN, Brian a Tom GRIFFITHS. <i>Algoritmy pro život: jak využít počítačové algoritmy při každodenním rozhodování.</i> Přeložil Filip DRLÍK. Brno : Jan Melvil Publishing, 2017. Pod povrchem. ISBN 978-80-7555-037-8.</ref> | + | Jedná se tak svým způsobem o aukci, kde dražitelé nabízejí za položku tolik, na kolik si ji opravdu váží a jakou pro ně má hodnotu. Zajímavý je také vztah s aukcí první nejvyšší vítězné nabídky. U této aukce posouvají účastníci své nabídky směrem dolů, aby se vyhnuli přeplacení. U Vickreyovy aukce tomu tak ale není potřeba – aukce sama nabídky optimálně upraví a to výrazně rychleji. Podle principu teorie her „rovnost výnosů“ se postupem času průměrná očekávaná prodejní cena v aukci s první nejvyšší vítěznou nabídkou přiblíží stejné hodnotě jako v případě aukce Vickreyovy. Tentýž účastník tak vyhraje položku za stejnou cenu, ale navíc <b>bez taktizování</b> kohokoli z účastníků. Tato aukce je i díky tomuto důvodu jedinečná.<ref name="Algoritmy4Life">CHRISTIAN, Brian a Tom GRIFFITHS. <i>Algoritmy pro život: jak využít počítačové algoritmy při každodenním rozhodování.</i> Přeložil Filip DRLÍK. Brno : Jan Melvil Publishing, 2017. Pod povrchem. ISBN 978-80-7555-037-8.</ref> |
Jednou z dalších vlastností, které tento typ aukce má, je, že pokud se aukce účastní málo dražitelů, bude pravděpodobně finální cena nižší. Pokud by na aukci byl pouze jeden účastník, musí být stanovena nejnižší částka, za kterou lze položku vydražit a která se pak chová jako druhá nejvyšší nabídka, kterou pak výherce musí po skončení aukce uhradit. Takové případy se ale většinou dějí pouze v digitálním světě, např. při reklamních aukcích, resp. při určování toho, jaká reklama se bude na stránkách návštěvníkovi zobrazovat.<ref name="GAUSS">KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: <i>What Is A Second Price Auction And How Does It Work?</i> [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/10/24/what-is-a-second-price-auction-and-how-does-it-work-video</ref> | Jednou z dalších vlastností, které tento typ aukce má, je, že pokud se aukce účastní málo dražitelů, bude pravděpodobně finální cena nižší. Pokud by na aukci byl pouze jeden účastník, musí být stanovena nejnižší částka, za kterou lze položku vydražit a která se pak chová jako druhá nejvyšší nabídka, kterou pak výherce musí po skončení aukce uhradit. Takové případy se ale většinou dějí pouze v digitálním světě, např. při reklamních aukcích, resp. při určování toho, jaká reklama se bude na stránkách návštěvníkovi zobrazovat.<ref name="GAUSS">KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: <i>What Is A Second Price Auction And How Does It Work?</i> [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/10/24/what-is-a-second-price-auction-and-how-does-it-work-video</ref> | ||
| Line 42: | Line 43: | ||
Hlavním benefitem je fakt, že výherce většinou zaplatí méně, než kolik nabídl. Na druhou stranu je aukce v této podobě nedostatečně transparentní kvůli nedostatku informací. To otvírá cestu k některým manipulacím:<ref name="GAUSS2">KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: <i>Common Problems With Second Price Auctions</i> [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/11/21/common-problems-with-second-price-auctions-video</ref> | Hlavním benefitem je fakt, že výherce většinou zaplatí méně, než kolik nabídl. Na druhou stranu je aukce v této podobě nedostatečně transparentní kvůli nedostatku informací. To otvírá cestu k některým manipulacím:<ref name="GAUSS2">KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: <i>Common Problems With Second Price Auctions</i> [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/11/21/common-problems-with-second-price-auctions-video</ref> | ||
| − | * SSP po sběru nabídek vloží falešnou nabídku mezi první dvě. Ovlivní tím tak výslednou částku, kterou výherce musí zaplatit, a zvýší tak výnos prodejce. Dražitel není schopen rozpoznat, že k manipulaci došlo a stále platí méně, než nabízel, ale platí více, než by podle výsledku aukce měl. | + | * SSP po sběru nabídek vloží <b>falešnou nabídku mezi první dvě</b>. Ovlivní tím tak výslednou částku, kterou výherce musí zaplatit, a zvýší tak výnos prodejce. Dražitel není schopen rozpoznat, že k manipulaci došlo a stále platí méně, než nabízel, ale platí více, než by podle výsledku aukce měl. |
| − | * Další možností k manipulaci je situace, kdy se aukce účastní pouze jediný účastník. Mechanismus aukce mnohdy neposkytuje poptávajícímu informaci o „bid floor“, tedy výši vyvolávací/výchozí ceny. Vzhledem k tomu, že se v případě jediného účastníka výchozí částka chová jako druhý účastník, stanovuje tak výslednou částku, kterou výherce musí uhradit. Manipulace spočívá v tom, že po skončení aukce si SSP upraví výchozí částku a tím zvýší výnos prodejce. Výherce nemá téměř žádnou šanci se o tomto kroku dozvědět. | + | * Další možností k manipulaci je situace, kdy se aukce účastní pouze jediný účastník. Mechanismus aukce mnohdy neposkytuje poptávajícímu informaci o „bid floor“, tedy výši vyvolávací/výchozí ceny. Vzhledem k tomu, že se v případě jediného účastníka výchozí částka chová jako druhý účastník, stanovuje tak výslednou částku, kterou výherce musí uhradit. Manipulace spočívá v tom, že po skončení aukce si <b>SSP upraví výchozí částku a tím zvýší výnos prodejce</b>. Výherce nemá téměř žádnou šanci se o tomto kroku dozvědět. |
Díky těmto možnostem manipulace DSP začínají přesouvat do aukcí s první nejvyšší vítěznou nabídkou, protože vědí přesně a ihned, kolik zaplatí. Doporučuje se tak všem DSP, než začnou spolupracovat s některými SSP, aby si zjistili, že dostávají informace o typu aukce, výchozí částku, a že může být SSP považována za důvěryhodnou. | Díky těmto možnostem manipulace DSP začínají přesouvat do aukcí s první nejvyšší vítěznou nabídkou, protože vědí přesně a ihned, kolik zaplatí. Doporučuje se tak všem DSP, než začnou spolupracovat s některými SSP, aby si zjistili, že dostávají informace o typu aukce, výchozí částku, a že může být SSP považována za důvěryhodnou. | ||
| Line 59: | Line 60: | ||
Z této původní aukce je také odvozeno několik dalších, které jsou pak vhodnější pro aukce komodit, resp. pro aukce s dělitelnými položkami. Používá se velmi podobný princip pro stanovení finální částky, kterou má výherce uhradit, ale již zde <u>není efekt stanovení vnitřní hodnoty</u>. Takto upravená aukce se nazývá <b>aukcí s jednotnou cenou</b>. Každý účastník určí, kolik jednotek daného zboží chce a kolik je za ně ochoten zaplatit. Následně se celé množství, které je předmětem aukce, rozdělí mezi účastníky s nejvyšší nabídkou podle jejich požadavků. Výherci pak zaplatí „pouze“ nejnižší výherní nabídku. Existují také další verze této aukce, které se většinou liší ve stanovení finální částky výherce.<ref name="UniformPrice">MALWEY, Paul F., ARCHIBALD Christine M., FLINN, Sean T. <i>Uniform-Price Auctions: Evaluation of the Treasury Experience. Office Of Market Finance</i> Washington, D.C., 2002, 20(220), 85. [cit. 2020-05-29]. Dostupné z: https://www.treasury.gov/resource-center/fin-mkts/Documents/final.pdf</ref> | Z této původní aukce je také odvozeno několik dalších, které jsou pak vhodnější pro aukce komodit, resp. pro aukce s dělitelnými položkami. Používá se velmi podobný princip pro stanovení finální částky, kterou má výherce uhradit, ale již zde <u>není efekt stanovení vnitřní hodnoty</u>. Takto upravená aukce se nazývá <b>aukcí s jednotnou cenou</b>. Každý účastník určí, kolik jednotek daného zboží chce a kolik je za ně ochoten zaplatit. Následně se celé množství, které je předmětem aukce, rozdělí mezi účastníky s nejvyšší nabídkou podle jejich požadavků. Výherci pak zaplatí „pouze“ nejnižší výherní nabídku. Existují také další verze této aukce, které se většinou liší ve stanovení finální částky výherce.<ref name="UniformPrice">MALWEY, Paul F., ARCHIBALD Christine M., FLINN, Sean T. <i>Uniform-Price Auctions: Evaluation of the Treasury Experience. Office Of Market Finance</i> Washington, D.C., 2002, 20(220), 85. [cit. 2020-05-29]. Dostupné z: https://www.treasury.gov/resource-center/fin-mkts/Documents/final.pdf</ref> | ||
| − | Další variantou této aukce je <b>VCG aukce</b> (Vickrey-Clark-Groves), která umožňuje prodávat více položek najednou. Nabídky jsou reprezentovány dvěma čísly, kde první číslo vyjadřuje požadovaný počet položek a číslo druhé pak cenu za tento jejich počet. Po obdržení všech nabídek se propočítají všechny jejich možné varianty. Z těch se vybere ta, která znamená největší výnos pro prodávajícího a následně jsou distribuovány předměty těm dražitelům, kteří nabídli největší částku, dokud takto nejsou všechny předměty rozdány. Jak je to s částkou, kterou výherci musí platit, když jich je tedy více? Ta se vypočte jako <u>rozdíl dvou sum</u>, kde první je suma ostatních výherních nabídek bez zohlednění daného výherce aukce (daný výherce jakoby ani neexistoval), a druhá je suma ostatních výherních nabídek se zohledněním daného výherce aukce. Každý výherce tak platí částku jinou. Zdá se to zamotané? K lepšímu pochopení slouží následující obrázek. V další kapitole jsou pak také příklady, jejichž účelem je prohloubení pochopení. | + | Další variantou této aukce je <b>VCG aukce</b> (Vickrey-Clark-Groves), která umožňuje prodávat více položek najednou. Nabídky jsou reprezentovány dvěma čísly, kde první číslo vyjadřuje požadovaný počet položek a číslo druhé pak cenu za tento jejich počet. Po obdržení všech nabídek se propočítají všechny jejich možné varianty. Z těch se vybere ta, která znamená největší výnos pro prodávajícího a následně jsou distribuovány předměty těm dražitelům, kteří nabídli největší částku, dokud takto nejsou všechny předměty rozdány. Jak je to s částkou, kterou výherci musí platit, když jich je tedy více? Ta se vypočte jako <u>rozdíl dvou sum</u>, kde první je suma ostatních výherních nabídek bez zohlednění daného výherce aukce (daný výherce jakoby ani neexistoval), a druhá je suma ostatních výherních nabídek se zohledněním daného výherce aukce. Každý výherce tak platí částku jinou. Zdá se to zamotané? K lepšímu pochopení slouží následující obrázek. V další kapitole jsou pak také příklady, jejichž účelem je další prohloubení pochopení a procvičení. |
Aukce VCG tak umožňuje rozšířit princip „čestnosti“ a vnitřní hodnoty předmětu na aukci s více položkami, což znamená, že taková aukce bude společensky optimální, tzn. přínos pro každou ze zúčastněných stran. Takový efekt je žádoucí hlavně v digitálním prostředí.<ref name="CombinatorialAuctions">CRAMTON, Peter, SHOHAM, Yoav, STEINBERG, Richard. <i>Combinatorial auctions.</i> Cambridge : MIT Press, 2006. ISBN 0-262-03342-9.</ref><ref name="VCG-Auction-Mechanism">YADUVANSHI, Santosh. LinkedIn.com: <i>How VCG Auction Mechanism Works Behind Facebook Ad.</i> [online]. [cit. 2020-05-29] Dostupné z: https://www.linkedin.com/pulse/how-vcg-auction-mechanism-works-behind-facebook-ad-santosh-yaduvanshi/</ref> | Aukce VCG tak umožňuje rozšířit princip „čestnosti“ a vnitřní hodnoty předmětu na aukci s více položkami, což znamená, že taková aukce bude společensky optimální, tzn. přínos pro každou ze zúčastněných stran. Takový efekt je žádoucí hlavně v digitálním prostředí.<ref name="CombinatorialAuctions">CRAMTON, Peter, SHOHAM, Yoav, STEINBERG, Richard. <i>Combinatorial auctions.</i> Cambridge : MIT Press, 2006. ISBN 0-262-03342-9.</ref><ref name="VCG-Auction-Mechanism">YADUVANSHI, Santosh. LinkedIn.com: <i>How VCG Auction Mechanism Works Behind Facebook Ad.</i> [online]. [cit. 2020-05-29] Dostupné z: https://www.linkedin.com/pulse/how-vcg-auction-mechanism-works-behind-facebook-ad-santosh-yaduvanshi/</ref> | ||
==Příklady== | ==Příklady== | ||
| − | |||
| − | |||
====Klasická Vickreyova aukce==== | ====Klasická Vickreyova aukce==== | ||
| − | + | Právě probíhá aukce, jejíž předmětem je historická poštovní známka. Uchazečů je celkem pět. Podle pravidel aukce každý z účastníků předloží svou nabídku v uzavřené obálce tak, aby ji nikdo jiný neviděl. Pověřená osoba poté otevře obálky a zjistí, kolik kdo nabídl: | |
| + | * Pavel - 490 000 Kč | ||
| + | * Josef - 320 000 Kč | ||
| + | * Jiří - 550 000 Kč | ||
| + | * Petr - 400 000 Kč | ||
| + | * Jan - 500 000 Kč | ||
| + | Nejvyšší částku nabídl Jiří a je proto výhercem aukce. Podle pravidel ale zaplatí druhou nejvyšší nabídku, kterou podal Jan a která činí 500 000 Kč. | ||
====VCG aukce==== | ====VCG aukce==== | ||
| − | + | Během VCG aukce se nabízejí celkem dvě reklamní zobrazení, o které budou soupeřit čtyři inzerenti. Každý inzerent může vyhrát maximálně jedno zobrazení. Inzerenti nabízejí částky 11, 7, 5 a 3 dolary. Výherci aukce tedy budou dva účastníci s nejvyššími nabídkami. Zatímco tyto nabídky činí 11 a 7 dolarů, oba zaplatí pouze po 5 dolarech. Zní to příliš dobře, aby to byla pravda? | |
| + | |||
| + | Na základě rovnice z předchozího obrázku si nyní přiblížíme výpočet ceny pro výherce. Pro prvního z nich, který nabízel 11 dolarů, se výhra spočte následovně:<ref name="VCG-Auction-Mechanism">YADUVANSHI, Santosh. LinkedIn.com: <i>How VCG Auction Mechanism Works Behind Facebook Ad.</i> [online]. [cit. 2020-05-29] Dostupné z: https://www.linkedin.com/pulse/how-vcg-auction-mechanism-works-behind-facebook-ad-santosh-yaduvanshi/</ref> | ||
| + | * První suma v rovnici nebere v úvahu vítěze, pro kterého se částka počítá. Tedy pro tuto chvíli první výherce neexistuje a aukci tak vyhráli účastníci s nabídkami 7 a 5 dolarů. Součet ostatních výherních nabídek v aukci je pak 7 + 5 + 0 = 12. | ||
| + | * Druhá suma již zahrnuje prvního výherce a spočte se jako 7 + 0 + 0 = 7. Zde je na levé straně rovnice pouze jedno nenulové číslo, protože kromě prvního výherce je tu už jen jeden další výherce. | ||
| + | * Ve výsledku tak podle vzorce zaplatí první výherce částku 12 - 7, což je 5 dolarů. Oproti původním 11 je to velký rozdíl. | ||
| + | |||
| + | Pro druhého výherce pak stejným postupem získáme hodnoty součtů: | ||
| + | * První suma nebere v úvahu nabídku 7 dolarů a proto je součet 11 + 5 + 0 = 16. | ||
| + | * Druhá suma druhého výherce bere v potaz a tak je součet 11 + 0 + 0 = 11. | ||
| + | * Ve výsledku to pak znamená 16 - 11 = 5, tedy druhý výherce, který nabízel 7 dolarů, zaplatí stejně jako první, a to částku 5 dolarů. | ||
====Aukce s jednotnou cenou==== | ====Aukce s jednotnou cenou==== | ||
| − | + | Předmětem aukce s jednotnou cenou je 100 špulek nití. Celkem se u aukce sešlo sedm zájemců. Podle pravidel aukce každý z účastníků předloží svou nabídku v uzavřené obálce tak, aby ji nikdo jiný neviděl. Pověřená osoba poté otevře obálky a zjistí, o jaké množství jednotek má kdo zájem a kolik kdo nabídl za jednotku. Podle počtu a náročnosti výpočtu, provede vyhodnocení pověřená osoba nebo počítač. V tomto případě se dá snadno určit, který z účastníků nabízí nejvíce. Vznikne tak pořadí: | |
| + | * Lukáš - 5 špulek, 300 Kč za jednotku | ||
| + | * Milan - 15 špulek, 220 Kč za jednotku | ||
| + | * David - 20 špulek, 180 Kč za jednotku | ||
| + | * František - 25 špulek, 150 Kč za jednotku | ||
| + | * Ondřej - 35 špulek, 140 Kč za jednotku | ||
| + | * Vojtěch - 30 špulek, 130 Kč za jednotku | ||
| + | * Svatopluk - 40 špulek, 100 Kč za jednotku | ||
| + | Nyní se zjišťuje, na koho se dostane. Podle toho se zjistí poslední výherní nabídka, která určí výslednou jednotnou cenu za jednotku. Následuje postup rozdělování špulek: | ||
| + | * Lukáš - dostane 5 špulek, zbývá 95 špulek | ||
| + | * Milan - dostane 15 špulek, zbývá 80 špulek | ||
| + | * David - dostane 20 špulek, zbývá 60 špulek | ||
| + | * František - dostane 25 špulek, zbývá 35 špulek | ||
| + | * Ondřej - dostane 35 špulek, nezbývají již žádné špulky. | ||
| + | Na Vojtěcha a Svatopluka se již nedostalo, jejich nabídky tedy nejsou výherní. Poslední výherní nabídka je ta Ondřejova, a tak každý z výherců zaplatí Ondřejovu nabízenou cenu za jednotku, tj. 140 Kč za jednu špulku. (Pozn.: pokud by špulek bylo 105, na Vojtěcha by tak zbylo 5 špulek, výsledná cena za jednotku by se určovala podle jednotkové ceny Vojtěcha, i když by Vojtěch dostal špulek pouze 5 a nikoli 30, jak původně chtěl.) | ||
| + | * Lukáš - zaplatí 5 špulek za 5 * 140 = 700 (Kč) | ||
| + | * Milan - zaplatí 15 špulek za 15 * 140 = 2100 (Kč) | ||
| + | * David - zaplatí 20 špulek za 20 * 140 = 2800 (Kč) | ||
| + | * František - zaplatí 25 špulek za 25 * 140 = 3500 (Kč) | ||
| + | * Ondřej - zaplatí 35 špulek za 35 * 140 = 4900 (Kč) | ||
| + | Existují různé variace této aukce, které se liší většinou v určení výsledné ceny za jednotku. Někdy je např. cena za jednotku určena první proherní nabídkou. V tomto příkladu by to znamenalo 130 Kč za jednotku, protože první nabídka, která nevyhrála patřila Vojtěchovi s jednotkovou cenou 130 Kč. | ||
==References== | ==References== | ||
<references/> | <references/> | ||
Latest revision as of 16:35, 30 May 2020
Contents
Úvod
Tento učební text se zabývá jedním specifickým typem aukce, kterým je aukce Vickreyova. Nejprve jsou popsány její charakteristiky, poté historie vzniku, dále je vysvětlen strategický postup při této aukci a nakonec je uvedeno několik příkladů, ať již těch jednodušších pro pochopení principu fungování, tak těch složitějších. Jsou také zmíněny případy, kdy se tento typ aukce používá v praxi, kterých překvapivě není málo.
Základní charakteristiky
Tomu, kdo se o aukce nijak více nezajímá, může následující popis připadat zbytečně složitý nebo na první pohled poněkud nesmyslný. Jak se ale v dalších odstavcích ukáže, vše má svůj smysl. Vickreyova aukce, častěji spíše nazývána aukcí druhé nejlepší nabídky, je jednokolová aukce probíhající obálkovou metodou, nabídky dražitelů jsou tak utajené. Nikdo tedy neví, jak si dražené položky cení ostatní účastníci. Druhým zásadním specifikem je, že ten, kdo nabídl částku nejvyšší, je sice vítěz, ale zaplatí ve skutečnosti pouze druhou nejvyšší nabízenou částku. Zpravidla se při této aukci draží jediný předmět. Ačkoli to nemusí být na první pohled jasné, tento typ aukce představuje unikátní přínosy. Jedním z nich je například rychlost, se kterou aukce probíhá. Dochází zde také k optimální alokaci zdrojů a to z toho důvodu, že dominantní strategií hráčů je nabídnutí skutečné hodnoty předmětu, resp. takové hodnoty, kterou pro daného hráče představuje.[1][2]
Historie
Jak již napovídá samotný název, tento typ aukce poprvé v roce 1961 důkladně popsal kanadský profesor a později také nositel Nobelovy ceny William Vickrey. Ocenění dostal za „zásadní příspěvek k ekonomické teorii stimulů v podmínkách asymetrických informací“[3], konkrétně za důkaz, že při tomto typu aukce je v nejlepším zájmu každého účastníka nabídnout maximální cenu, kterou je ještě ochoten zaplatit.[4]
Vlastnosti aukce a strategie dražitelů
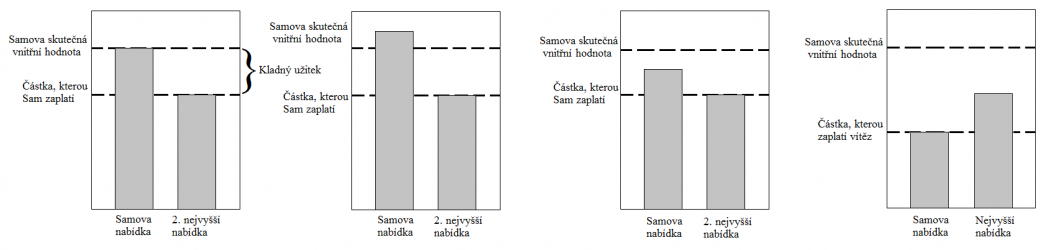
Vickreyova aukce má z hlediska teorie her spoustu zajímavých vlastností. Zvláště zajímavá je jedna vlastnost, díky které jsou účastníci vybízení k tomu, aby postupovali čestně. Ve skutečnosti nejlepší strategií pro dražitele je právě nabídnout svou „subjektivní“ skutečnou vnitřní hodnotu, kterou pro ně daná položka představuje, resp. nakolik si jí cení.[1] Obrázky spolu s jejich popisem napomáhají vysvětlit, proč je ve Vickreyově aukci nejlepší strategií čestnost a proč nemusí účastníci brát ohled na ostatní. Pro demonstrační účely byl vybrán jeden účastník aukce jménem Sam.
Obrázek vpravo zachycuje Sama ve výchozí situaci jakožto výherce aukce. Zleva první situace ukazuje stav, který je pro Vickreyovu aukci typický. Reflektuje také onu dominantní strategii – účastníci nabízejí tolik, nakolik si dané položky skutečně cení. V této situaci Sam vyhraje aukci, jeho užitek je navíc reprezentován rozdílem dvou nabídek, protože výherce Sam uhradí tu druhou. Následující situace ukazuje, že pokud Sam zvýší svou nabídku, nic se pro něj nezmění – aukci stále vyhraje on a cena, kterou musí zaplatit, zůstane stejná. Navíc se zde vystavuje riziku, že při vyšších nabídkách ostatních účastníků zaplatí více, než si dané položky cení on sám. Zleva třetí situace ukazuje, že ani snižování jeho nabídky by nemělo žádný vliv na výsledek, pokud by ovšem snížení nevedlo až do poslední situace. Zde už Sam není výhercem aukce, jeho nabídka pouze určuje částku, kterou má výherce uhradit. Samův užitek je v tomto případě nulový. Ve všech předchozích případech byl kladný.[1]
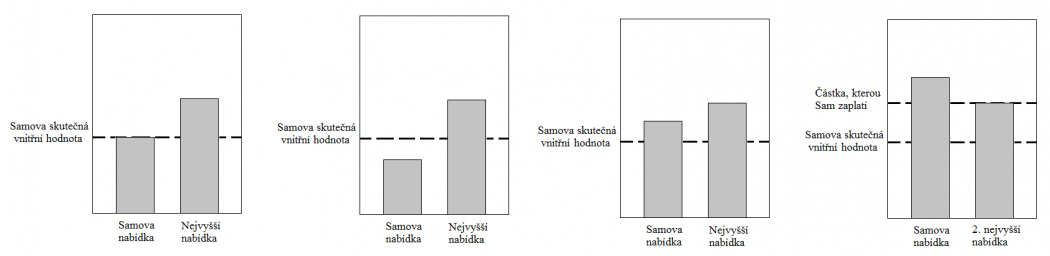
Na dalším obrázku Sam jako druhý v pořadí prohrává aukci. Zleva první situace ukazuje tento výchozí stav. Další dvě situace ukazují, že snižování ani zvyšování nabídky nemá na výsledek vliv. Pokud ale Sam bude jednat neupřímně a zvýší svou nabídku tak, že vyhraje a zaplatí druhou nejvyšší částku, bude muset tak uhradit více, než je jeho skutečná vnitřní hodnota, resp. nakolik ohodnotil položku on sám. Pomocí těchto situací je dokázáno, že nejlepší nabídkou je ta, která odráží skutečnou vnitřní hodnotu pro daného účastníka. Pokud se bude nabídka lišit od skutečné vnitřní hodnoty, nebude to mít žádný vliv nebo bude muset účastník zaplatit více, než pro něj daná položka představuje. Z toho vyplývá, že stanovení nabídky ve výši představující vnitřní skutečnou hodnotu, je dominantní strategií. Za povšimnutí stojí, že během dokazování nedošlo k popisu žádného vztahu mezi nabídkami ostatních účastníků nebo jejich vlastních ohodnocení.[1] Díky těmto vlastnostem je Vickreyova aukce tzv. „odolná vůči strategiím“ nebo prostě a jednoduše „pravdivá“. Proto při Vickreyově aukci představuje upřímnost nejlepší strategii. Navíc v případě, kdy ostatní dražitelé nepostupují čestně, je tato dominantní strategie upřímnosti ještě výhodnější.[5]
Jedná se tak svým způsobem o aukci, kde dražitelé nabízejí za položku tolik, na kolik si ji opravdu váží a jakou pro ně má hodnotu. Zajímavý je také vztah s aukcí první nejvyšší vítězné nabídky. U této aukce posouvají účastníci své nabídky směrem dolů, aby se vyhnuli přeplacení. U Vickreyovy aukce tomu tak ale není potřeba – aukce sama nabídky optimálně upraví a to výrazně rychleji. Podle principu teorie her „rovnost výnosů“ se postupem času průměrná očekávaná prodejní cena v aukci s první nejvyšší vítěznou nabídkou přiblíží stejné hodnotě jako v případě aukce Vickreyovy. Tentýž účastník tak vyhraje položku za stejnou cenu, ale navíc bez taktizování kohokoli z účastníků. Tato aukce je i díky tomuto důvodu jedinečná.[5]
Jednou z dalších vlastností, které tento typ aukce má, je, že pokud se aukce účastní málo dražitelů, bude pravděpodobně finální cena nižší. Pokud by na aukci byl pouze jeden účastník, musí být stanovena nejnižší částka, za kterou lze položku vydražit a která se pak chová jako druhá nejvyšší nabídka, kterou pak výherce musí po skončení aukce uhradit. Takové případy se ale většinou dějí pouze v digitálním světě, např. při reklamních aukcích, resp. při určování toho, jaká reklama se bude na stránkách návštěvníkovi zobrazovat.[6]
Využití v praxi
I když není aukce druhé nejlepší nabídky tolik využívána ve skutečném světě mezi lidmi, je hojně používána ve světě digitálním a to právě z důvodu rychlosti. Tento typ aukce lze implementovat i automatizovat v mnoha variantách.
Reálné prostředí
Díky tomu, že tato specifická aukce upřednostňuje skupinový prospěch na úkor prodávajícího, využívá se přímo mezi lidmi méně. Jedním z takových ojedinělých případů jsou např. filatelistické skupiny, které se věnují sběru známek. Již od konce 19. století, kdy zde tato aukce byla údajně poprvé použita, je Vickreyova aukce preferovaná dodnes.[7]
Online marketing – reklamy
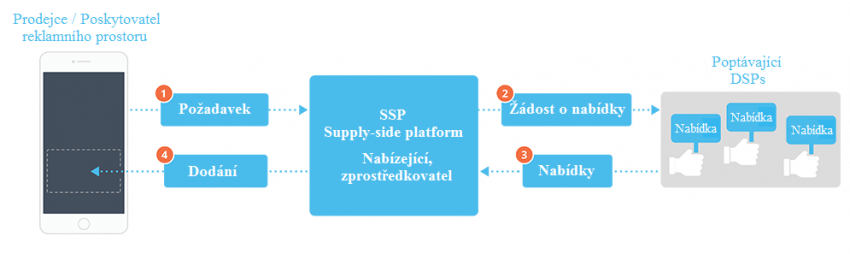
Nejznámějším jsou zde pravděpodobně Google AdWorks nebo také reklamní aukce na Yahoo. Zde se jedná o modifikovanou Vickreyovu aukci, protože zde hraje roli také relevance reklamy, klíčových slov a obsah stránky a výše nabídky tak není jediné kritérium při určování výherce.[9] Tento plně automatizovaný mechanismus umožňuje nabízet reklamní prostor prostřednictvím aukcí. Na tomto místě je nutné si přiblížit dva pojmy:[10]
- SSP – supply-side platform, neboli nabízející, je platforma, která je přímo propojena s vydavateli, resp. aplikacemi či webovými stránkami s volným reklamním prostorem. Prostřednictvím aukcí platforma tento prostor nabízí. Cílem SSP je maximalizovat výdělky reklam majitelů stránek nebo aplikací.
- DSP – demand-side platform, je platforma, která umožňuje správu více reklamních aukcí v rámci jednoho rozhraní. Poptávající, resp. dražitelé, jsou pak různé reklamní agentury nebo přímo jednotliví inzerenti.
Hlavním benefitem je fakt, že výherce většinou zaplatí méně, než kolik nabídl. Na druhou stranu je aukce v této podobě nedostatečně transparentní kvůli nedostatku informací. To otvírá cestu k některým manipulacím:[11]
- SSP po sběru nabídek vloží falešnou nabídku mezi první dvě. Ovlivní tím tak výslednou částku, kterou výherce musí zaplatit, a zvýší tak výnos prodejce. Dražitel není schopen rozpoznat, že k manipulaci došlo a stále platí méně, než nabízel, ale platí více, než by podle výsledku aukce měl.
- Další možností k manipulaci je situace, kdy se aukce účastní pouze jediný účastník. Mechanismus aukce mnohdy neposkytuje poptávajícímu informaci o „bid floor“, tedy výši vyvolávací/výchozí ceny. Vzhledem k tomu, že se v případě jediného účastníka výchozí částka chová jako druhý účastník, stanovuje tak výslednou částku, kterou výherce musí uhradit. Manipulace spočívá v tom, že po skončení aukce si SSP upraví výchozí částku a tím zvýší výnos prodejce. Výherce nemá téměř žádnou šanci se o tomto kroku dozvědět.
Díky těmto možnostem manipulace DSP začínají přesouvat do aukcí s první nejvyšší vítěznou nabídkou, protože vědí přesně a ihned, kolik zaplatí. Doporučuje se tak všem DSP, než začnou spolupracovat s některými SSP, aby si zjistili, že dostávají informace o typu aukce, výchozí částku, a že může být SSP považována za důvěryhodnou.
Datové sítě a pakety
Dalším zajímavým příkladem z praxe, kde se princip této aukce využívá, je směrování paketů v datových sítích. Vzhledem k tomu, že uzly v síti nemohou vždy splnit všechny požadavky, je nutné trasy mezi nimi definovat. Tzv. sobecké datové uzly v síti jsou takové, které nijak nespolupracují s uzly ostatními. V síti jsou páry, které potřebují šířku pásma, jež jim musí být přiřazena. Uzly právě tuto šířku pásma nabízejí. Pár pak nabízí platbu za potřebnou šířku pásma. Díky tomu, že tyto transakce jsou prováděny automaticky a se stanovenými cenami, jeví se Vickreyova aukce jako vhodná volba. Navíc se tímto způsobem zabrání přeplacení a umožní nalezení nejvhodnějších cest v síti. Pomocí principu této aukce se tak docílí kooperace mezi uzly.[12]
Telekomunikace
Podobný princip může být také aplikován v oblasti telekomunikací při směrování hovorů. V takovém systému jsou agenti, kteří reprezentují různé síťové zdroje, orientovaní na své cíle, jsou vlastněni rozdílnými společnostmi a koordinují své alokace zdrojů bez předem definované kooperace. Následná implementace aukčního principu má pak vést ke snížení blokování hovorů v síti.[13]
Modifikovaná Vickreyova aukce
Z této původní aukce je také odvozeno několik dalších, které jsou pak vhodnější pro aukce komodit, resp. pro aukce s dělitelnými položkami. Používá se velmi podobný princip pro stanovení finální částky, kterou má výherce uhradit, ale již zde není efekt stanovení vnitřní hodnoty. Takto upravená aukce se nazývá aukcí s jednotnou cenou. Každý účastník určí, kolik jednotek daného zboží chce a kolik je za ně ochoten zaplatit. Následně se celé množství, které je předmětem aukce, rozdělí mezi účastníky s nejvyšší nabídkou podle jejich požadavků. Výherci pak zaplatí „pouze“ nejnižší výherní nabídku. Existují také další verze této aukce, které se většinou liší ve stanovení finální částky výherce.[15]
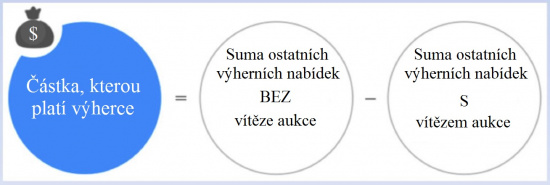
Další variantou této aukce je VCG aukce (Vickrey-Clark-Groves), která umožňuje prodávat více položek najednou. Nabídky jsou reprezentovány dvěma čísly, kde první číslo vyjadřuje požadovaný počet položek a číslo druhé pak cenu za tento jejich počet. Po obdržení všech nabídek se propočítají všechny jejich možné varianty. Z těch se vybere ta, která znamená největší výnos pro prodávajícího a následně jsou distribuovány předměty těm dražitelům, kteří nabídli největší částku, dokud takto nejsou všechny předměty rozdány. Jak je to s částkou, kterou výherci musí platit, když jich je tedy více? Ta se vypočte jako rozdíl dvou sum, kde první je suma ostatních výherních nabídek bez zohlednění daného výherce aukce (daný výherce jakoby ani neexistoval), a druhá je suma ostatních výherních nabídek se zohledněním daného výherce aukce. Každý výherce tak platí částku jinou. Zdá se to zamotané? K lepšímu pochopení slouží následující obrázek. V další kapitole jsou pak také příklady, jejichž účelem je další prohloubení pochopení a procvičení. Aukce VCG tak umožňuje rozšířit princip „čestnosti“ a vnitřní hodnoty předmětu na aukci s více položkami, což znamená, že taková aukce bude společensky optimální, tzn. přínos pro každou ze zúčastněných stran. Takový efekt je žádoucí hlavně v digitálním prostředí.[16][14]
Příklady
Klasická Vickreyova aukce
Právě probíhá aukce, jejíž předmětem je historická poštovní známka. Uchazečů je celkem pět. Podle pravidel aukce každý z účastníků předloží svou nabídku v uzavřené obálce tak, aby ji nikdo jiný neviděl. Pověřená osoba poté otevře obálky a zjistí, kolik kdo nabídl:
- Pavel - 490 000 Kč
- Josef - 320 000 Kč
- Jiří - 550 000 Kč
- Petr - 400 000 Kč
- Jan - 500 000 Kč
Nejvyšší částku nabídl Jiří a je proto výhercem aukce. Podle pravidel ale zaplatí druhou nejvyšší nabídku, kterou podal Jan a která činí 500 000 Kč.
VCG aukce
Během VCG aukce se nabízejí celkem dvě reklamní zobrazení, o které budou soupeřit čtyři inzerenti. Každý inzerent může vyhrát maximálně jedno zobrazení. Inzerenti nabízejí částky 11, 7, 5 a 3 dolary. Výherci aukce tedy budou dva účastníci s nejvyššími nabídkami. Zatímco tyto nabídky činí 11 a 7 dolarů, oba zaplatí pouze po 5 dolarech. Zní to příliš dobře, aby to byla pravda?
Na základě rovnice z předchozího obrázku si nyní přiblížíme výpočet ceny pro výherce. Pro prvního z nich, který nabízel 11 dolarů, se výhra spočte následovně:[14]
- První suma v rovnici nebere v úvahu vítěze, pro kterého se částka počítá. Tedy pro tuto chvíli první výherce neexistuje a aukci tak vyhráli účastníci s nabídkami 7 a 5 dolarů. Součet ostatních výherních nabídek v aukci je pak 7 + 5 + 0 = 12.
- Druhá suma již zahrnuje prvního výherce a spočte se jako 7 + 0 + 0 = 7. Zde je na levé straně rovnice pouze jedno nenulové číslo, protože kromě prvního výherce je tu už jen jeden další výherce.
- Ve výsledku tak podle vzorce zaplatí první výherce částku 12 - 7, což je 5 dolarů. Oproti původním 11 je to velký rozdíl.
Pro druhého výherce pak stejným postupem získáme hodnoty součtů:
- První suma nebere v úvahu nabídku 7 dolarů a proto je součet 11 + 5 + 0 = 16.
- Druhá suma druhého výherce bere v potaz a tak je součet 11 + 0 + 0 = 11.
- Ve výsledku to pak znamená 16 - 11 = 5, tedy druhý výherce, který nabízel 7 dolarů, zaplatí stejně jako první, a to částku 5 dolarů.
Aukce s jednotnou cenou
Předmětem aukce s jednotnou cenou je 100 špulek nití. Celkem se u aukce sešlo sedm zájemců. Podle pravidel aukce každý z účastníků předloží svou nabídku v uzavřené obálce tak, aby ji nikdo jiný neviděl. Pověřená osoba poté otevře obálky a zjistí, o jaké množství jednotek má kdo zájem a kolik kdo nabídl za jednotku. Podle počtu a náročnosti výpočtu, provede vyhodnocení pověřená osoba nebo počítač. V tomto případě se dá snadno určit, který z účastníků nabízí nejvíce. Vznikne tak pořadí:
- Lukáš - 5 špulek, 300 Kč za jednotku
- Milan - 15 špulek, 220 Kč za jednotku
- David - 20 špulek, 180 Kč za jednotku
- František - 25 špulek, 150 Kč za jednotku
- Ondřej - 35 špulek, 140 Kč za jednotku
- Vojtěch - 30 špulek, 130 Kč za jednotku
- Svatopluk - 40 špulek, 100 Kč za jednotku
Nyní se zjišťuje, na koho se dostane. Podle toho se zjistí poslední výherní nabídka, která určí výslednou jednotnou cenu za jednotku. Následuje postup rozdělování špulek:
- Lukáš - dostane 5 špulek, zbývá 95 špulek
- Milan - dostane 15 špulek, zbývá 80 špulek
- David - dostane 20 špulek, zbývá 60 špulek
- František - dostane 25 špulek, zbývá 35 špulek
- Ondřej - dostane 35 špulek, nezbývají již žádné špulky.
Na Vojtěcha a Svatopluka se již nedostalo, jejich nabídky tedy nejsou výherní. Poslední výherní nabídka je ta Ondřejova, a tak každý z výherců zaplatí Ondřejovu nabízenou cenu za jednotku, tj. 140 Kč za jednu špulku. (Pozn.: pokud by špulek bylo 105, na Vojtěcha by tak zbylo 5 špulek, výsledná cena za jednotku by se určovala podle jednotkové ceny Vojtěcha, i když by Vojtěch dostal špulek pouze 5 a nikoli 30, jak původně chtěl.)
- Lukáš - zaplatí 5 špulek za 5 * 140 = 700 (Kč)
- Milan - zaplatí 15 špulek za 15 * 140 = 2100 (Kč)
- David - zaplatí 20 špulek za 20 * 140 = 2800 (Kč)
- František - zaplatí 25 špulek za 25 * 140 = 3500 (Kč)
- Ondřej - zaplatí 35 špulek za 35 * 140 = 4900 (Kč)
Existují různé variace této aukce, které se liší většinou v určení výsledné ceny za jednotku. Někdy je např. cena za jednotku určena první proherní nabídkou. V tomto příkladu by to znamenalo 130 Kč za jednotku, protože první nabídka, která nevyhrála patřila Vojtěchovi s jednotkovou cenou 130 Kč.
References
- ↑ 1.0 1.1 1.2 1.3 JACKSON, Matthew O., LEYTON-BROWN, Kevin, SHOHAM, Yoav. Game Theory Online [online]. 2018 [cit. 2020-05-29]. Dostupné z: http://www.game-theory-class.org/
- ↑ LUCKING-REILEY, David. Vickrey Auctions in Practice: From Nineteenth-Century Philately to Twenty-First-Century E-Commerce. Journal of Economic Perspectives [online]. 2000, 14(3), 183-192 [cit. 2020-05-29]. DOI: 10.1257/jep.14.3.183. ISSN 0895-3309. Dostupné z: http://pubs.aeaweb.org/doi/10.1257/jep.14.3.183
- ↑ —. Wikipedia.org: List of Nobel Memorial Prize laureates in Economics. [online]. [cit. 2020-05-29]. Dostupné z: https://en.wikipedia.org/wiki/List_of_Nobel_Memorial_Prize_laureates_in_Economics
- ↑ ARIELY, Dan. Jak drahé je zdarma: proč chytří lidé přijímají špatná rozhodnutí : iracionální faktory v ekonomice i v životě. Praha : Práh, 2009. ISBN 978-80-7252-239-2.
- ↑ 5.0 5.1 CHRISTIAN, Brian a Tom GRIFFITHS. Algoritmy pro život: jak využít počítačové algoritmy při každodenním rozhodování. Přeložil Filip DRLÍK. Brno : Jan Melvil Publishing, 2017. Pod povrchem. ISBN 978-80-7555-037-8.
- ↑ KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: What Is A Second Price Auction And How Does It Work? [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/10/24/what-is-a-second-price-auction-and-how-does-it-work-video
- ↑ LUCKING-REILEY, David. Vickrey Auctions in Practice: From Nineteenth-Century Philately to Twenty-First-Century E-Commerce. Journal of Economic Perspectives [online]. 2000, 14(3), 183-192 [cit. 2020-05-29]. DOI: 10.1257/jep.14.3.183. ISSN 0895-3309. Dostupné z: http://pubs.aeaweb.org/doi/10.1257/jep.14.3.183
- ↑ —. Smaato.com: Real-Time Bidding (RTB): The Complete Guide [online]. [cit. 2020-05-29]. Dostupné z: https://www.smaato.com/real-time-bidding/
- ↑ —. YouTube.com: Google Ads Auction Explained. [online]. [cit. 2020-05-29]. Dostupné z: https://www.youtube.com/watch?v=JLf2LwA2oek
- ↑ REICH, Courtney. Smaato.com: What’s the Difference Between an SSP and a DSP? [online]. [cit. 2020-05-29]. Dostupné z: https://www.smaato.com/blog/whats-the-difference-between-an-ssp-and-a-dsp/
- ↑ KAPLAN, Matt, GAUSS, Ryan. Inmobi.com: Common Problems With Second Price Auctions [online]. [cit. 2020-05-29]. Dostupné z: https://www.inmobi.com/blog/2018/11/21/common-problems-with-second-price-auctions-video
- ↑ ZHOU, Haojie, Ka-Cheong LEUNG and Victor O. K. LI. Auction-Based Schemes for Multipath Routing In Selfish Networks. 2013 IEEE Wireless Communications and Networking Conference (WCNC) [online]. The University of Hong Kong, 2013 [cit. 2020-05-29]. Dostupné z: https://www.eee.hku.hk/~kcleung/papers/conferences/auction-based_multipath_routing:WCNC_2013/06554864.pdf
- ↑ GIBNEY, M. A., JENNINGS, N. R., VRIEND, N. J. Market-Based Call Routing in Telecommunications Networks using Adaptive Pricing and Real Bidding [online]. University of London, 2001. [cit. 2020-05-29]. DOI: 10.1002/0470841818.ch18. Dostupné z: http://nvriend.econ.qmul.ac.uk/pub/alife.pdf
- ↑ 14.0 14.1 14.2 YADUVANSHI, Santosh. LinkedIn.com: How VCG Auction Mechanism Works Behind Facebook Ad. [online]. [cit. 2020-05-29] Dostupné z: https://www.linkedin.com/pulse/how-vcg-auction-mechanism-works-behind-facebook-ad-santosh-yaduvanshi/
- ↑ MALWEY, Paul F., ARCHIBALD Christine M., FLINN, Sean T. Uniform-Price Auctions: Evaluation of the Treasury Experience. Office Of Market Finance Washington, D.C., 2002, 20(220), 85. [cit. 2020-05-29]. Dostupné z: https://www.treasury.gov/resource-center/fin-mkts/Documents/final.pdf
- ↑ CRAMTON, Peter, SHOHAM, Yoav, STEINBERG, Richard. Combinatorial auctions. Cambridge : MIT Press, 2006. ISBN 0-262-03342-9.