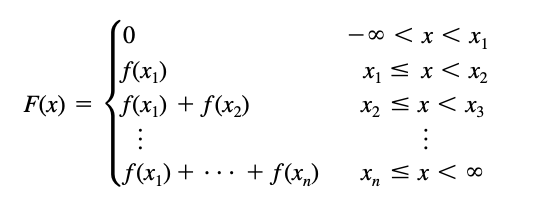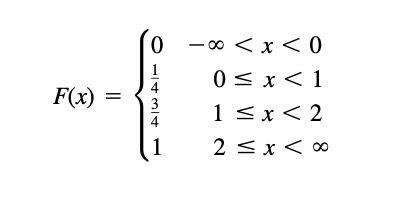Difference between revisions of "Probability distributions"
(→Cumulative distribution function) |
(→Discrete probability distribution) |
||
| Line 70: | Line 70: | ||
==== The Poisson Distributions ==== | ==== The Poisson Distributions ==== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Absolutely continuous probability distribution== | == Absolutely continuous probability distribution== | ||
Revision as of 18:11, 30 May 2023
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment.[1][2] It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space).[3]
Contents
Introduction
Probability is the science of uncertainty. It provides precise mathematical rules for understanding and analyzing our own ignorance. It does not tell us tomorrow’s weather or next week’s stock prices; rather, it gives us a framework for working with our limited knowledge and for making sensible decisions based on what we do and do not know. (citee)
Terminology
Sample space
In probability theory, the sample space refers to the set of all possible outcomes of a random experiment. It is denoted by the symbol Ω (capital omega).
- Let's consider an example of rolling a fair six-sided die. The sample space in this case would be {1, 2, 3, 4, 5, 6}, as these are the possible outcomes of the experiment. Each number represents the face of the die that may appear when it is rolled.
Random variable
Random variable takes values from a sample space. In contrast, probabilities describe which values and set of values are more likely to be taken out of the sample space. Random variable must be quantified, therefore, it assigns a numerical value to each possible outcome in the sample space.
- For example, if the sample space for flipping a coin is {heads, tails}, then we can assign a random variable Y such that Y = 1 when heads land and Y = 0 when tails land. However, we can assign any number for these variables. 0 and 1 are just more convenient.
- Because random variables are defined to be functions of the outcome s, and because the outcome s is assumed to be random (i.e., to take on different values with different probabilities), it follows that the value of a random variable will itself be random (as the name implies).
Specifically, if X is a random variable, then what is the probability that X will equal some particular value x? Well, X = x precisely when the outcome s is chosen such that X(s) = x.
- Exercise
- Suppose that a coin is tossed twice so that the sample space is S = {HH, HT, TH, TT}. Let X represent the number of heads that can come up. With each sample point we can associate a number for X as shown in Table 1. Thus, for example, in the case of HH (i.e., 2 heads), X = 2 while for TH (1 head), X = 1. It follows that X is a random variable.
Probability mass function (PMF)
The probability mass function, denoted as P(X = x), is used for discrete random variables. It assigns probabilities to each possible value that the random variable can take. The PMF gives the probability that the random variable equals a specific value.
Cumulative distribution function (CDF)
The cumulative distribution function, denoted as F(x), describes the probability that a random variable takes on a value less than or equal to a given value x. It gives the cumulative probability up to a specific point.
Probability density function (PDF)
he probability density function (PDF) is a function used to describe the probability distribution of a continuous random variable. Unlike discrete random variables, which have a countable set of possible values, continuous random variables can take on any value within a specified range.
The PDF, denoted as f(x), represents the density of the probability distribution of a continuous random variable at a given point x. It provides information about the likelihood of the random variable taking on a specific value or falling within a specific range of values.
Distribution Functions for Random Variables
The distribution function provides important information about the probabilities associated with different values of a random variable. It can be used to calculate probabilities for specific events or to obtain other statistical properties of the random variable.
- It gives the probability that the random variable takes on a value less than or equal to a given value.
The distribution function of a random variable X, denoted as F(x), is defined as:
- F(x) = P(X ≤ x)
where x is any real number, and P(X ≤ x) is the probability that the random variable X is less than or equal to x.
- Discrete probability distribution: for many random variables with finitely or countably infinitely many values.
- Probability mass function (pmf): function that gives the probability that a discrete random variable is equal to some value.
- Frequency distribution: a table that displays the frequency of various outcomes Template:Em.
- Relative frequency distribution: a frequency distribution where each value has been divided (normalized) by a number of outcomes in a sample (i.e. sample size).
- Categorical distribution: for discrete random variables with a finite set of values.
Distribution Functions for Discrete Random Variables
If X takes on only a finite number of values x1, x2, . . . , xn, then the distribution function is given by
Distribution Functions for Continuous Variables
Special Probability Distributions
The Binomial Distributions
The Normal Distributions
The Poisson Distributions
Absolutely continuous probability distribution
An absolutely continuous probability distribution is a probability distribution on the real numbers with uncountably many possible values, such as a whole interval in the real line, and where the probability of any event can be expressed as an integral.[4] More precisely, a real random variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} has an absolutely continuous probability distribution if there is a function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f: \Reals \to [0, \infty]} such that for each interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b] \subset \mathbb{R}} the probability of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} belonging to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} is given by the integral of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} over Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I} :[5][6] Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .} This is the definition of a probability density function, so that absolutely continuous probability distributions are exactly those with a probability density function. In particular, the probability for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} to take any single value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} (that is, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \le X \le a} ) is zero, because an integral with coinciding upper and lower limits is always equal to zero. If the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle [a,b]} is replaced by any measurable set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} , the according equality still holds: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X \in A) = \int_A f(x) \, dx .}
An absolutely continuous random variable is a random variable whose probability distribution is absolutely continuous.
There are many examples of absolutely continuous probability distributions: normal, uniform, chi-squared, and others.
Cumulative distribution function
Absolutely continuous probability distributions as defined above are precisely those with an absolutely continuous cumulative distribution function. In this case, the cumulative distribution function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F} has the form Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} is a density of the random variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} with regard to the distribution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P} .
Note on terminology: Absolutely continuous distributions ought to be distinguished from continuous distributions, which are those having a continuous cumulative distribution function. Every absolutely continuous distribution is a continuous distribution but the inverse is not true, there exist singular distributions, which are neither absolutely continuous nor discrete nor a mixture of those, and do not have a density. An example is given by the Cantor distribution. Some authors however use the term "continuous distribution" to denote all distributions whose cumulative distribution function is absolutely continuous, i.e. refer to absolutely continuous distributions as continuous distributions.[7]
For a more general definition of density functions and the equivalent absolutely continuous measures see absolutely continuous measure.
- ↑ Spiegel, M. R., Schiller, J. T., & Srinivasan, A. (2001). Probability and Statistics : based on Schaum’s outline of Probability and Statistics by Murray R. Spiegel, John Schiller, and R. Alu Srinivasan. https://ci.nii.ac.jp/ncid/BA77714681
- ↑ Spiegel, M. R., Schiller, J. T., & Srinivasan, A. (2001). Probability and Statistics : based on Schaum’s outline of Probability and Statistics by Murray R. Spiegel, John Schiller, and R. Alu Srinivasan. https://ci.nii.ac.jp/ncid/BA77714681
- ↑ Spiegel, M. R., Schiller, J. T., & Srinivasan, A. (2001). Probability and Statistics : based on Schaum’s outline of Probability and Statistics by Murray R. Spiegel, John Schiller, and R. Alu Srinivasan. https://ci.nii.ac.jp/ncid/BA77714681
- ↑ Spiegel, M. R., Schiller, J. T., & Srinivasan, A. (2001). Probability and Statistics : based on Schaum’s outline of Probability and Statistics by Murray R. Spiegel, John Schiller, and R. Alu Srinivasan. https://ci.nii.ac.jp/ncid/BA77714681
- ↑ Chapter 3.2 of Template:Harvp
- ↑ Template:Cite web
- ↑ Spiegel, M. R., Schiller, J. T., & Srinivasan, A. (2001). Probability and Statistics : based on Schaum’s outline of Probability and Statistics by Murray R. Spiegel, John Schiller, and R. Alu Srinivasan. https://ci.nii.ac.jp/ncid/BA77714681