Difference between revisions of "User:ZdenekP"
| (8 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
'''Aktéři:''' | '''Aktéři:''' | ||
| − | * | + | * <code>passengers</code> (pasažéři) – modří, každé patro obsahuje 12 pasažérů (celkem 144). |
| − | * | + | * <code>elevator</code> (výtah) – jeden červený výtah, začíná v přízemí (y=0). |
'''Vlastnosti pasažéra:''' | '''Vlastnosti pasažéra:''' | ||
| Line 37: | Line 37: | ||
* Přesun výtahu zahrnuje zrychlení a zpomalení (podle vzdálenosti k cílovému patru) | * Přesun výtahu zahrnuje zrychlení a zpomalení (podle vzdálenosti k cílovému patru) | ||
| − | [[File:simzp-elevator.png|left| | + | [[File:simzp-elevator.png|left|1000px|náhled|Simulační prostředí v NetLogo]] |
<br clear="all"/> | <br clear="all"/> | ||
| Line 90: | Line 90: | ||
|} | |} | ||
| − | + | == '''Závěr''' == | |
Simulace ukázala, že zvolený algoritmus řízení výtahu významně ovlivňuje průběh přepravy cestujících během ranní špičky. | Simulace ukázala, že zvolený algoritmus řízení výtahu významně ovlivňuje průběh přepravy cestujících během ranní špičky. | ||
Při použití klasického algoritmu s preferencí směru dolů (''look – down first'') byla průměrná doba čekání vyšší (57 s), avšak doba jízdy kratší (56 s). Celkový čas přesunu činil 110 sekund. Naopak při algoritmu ''look – up first'' (nejprve nahoru) byla doba čekání nižší (42 s), ale cestující strávili více času jízdou (64 s). Celková doba přesunu byla mírně nižší (107 s). | Při použití klasického algoritmu s preferencí směru dolů (''look – down first'') byla průměrná doba čekání vyšší (57 s), avšak doba jízdy kratší (56 s). Celkový čas přesunu činil 110 sekund. Naopak při algoritmu ''look – up first'' (nejprve nahoru) byla doba čekání nižší (42 s), ale cestující strávili více času jízdou (64 s). Celková doba přesunu byla mírně nižší (107 s). | ||
| − | Z výsledků vyplývá, že | + | Z výsledků vyplývá, že algoritmus "nejdříve nahoru" přinesl nižší průměrnou dobu čekání i o něco kratší celkový čas přesunu. Tento přístup je tedy v podmínkách simulované ranní špičky mírně efektivnější, přestože cestující urazí delší trasu. Optimalizace směru pohybu výtahu podle očekávaného zatížení pater se tedy jeví jako účinná strategie. |
=== Potenciál a využitelnost simulace === | === Potenciál a využitelnost simulace === | ||
| − | Simulace výtahu má široký potenciál jak pro výukové, tak i praktické účely. | + | Simulace výtahu má široký potenciál jak pro výukové, tak i praktické účely. Ve výukovém kontextu slouží jako názorný příklad agentově orientovaného modelování, kde lze demonstrovat interakci mezi jednotlivými entitami (pasažéři, výtah) a vliv různých algoritmů řízení na celkovou efektivitu systému. V praxi by podobný model mohl být dále rozšířen a využit například pro optimalizaci výtahových systémů ve vícepodlažních budovách, testování různých řídicích strategií, nebo simulaci zatížení během špiček. S drobnými úpravami by bylo možné model přizpůsobit také pro více výtahů nebo různá pravidla chování cestujících, což by umožnilo reálnější nasazení v oblasti inteligentních budov a facility managementu. |
| + | |||
| + | === Kód netlogo === | ||
| + | [[File:elevator.nlogo]] | ||
| + | |||
| + | === Reference === | ||
| + | * [https://download.peters-research.com/library/Measuring_and_Simulating_Elevator_Passengers_in_Existing_Buildings.pdf Vytížení výtahu v kancelářské budově] | ||
| + | * [https://liftescalatorlibrary.org/paper_indexing/papers/00000051.pdf Vytížení výtahu v obytné budově] | ||
| + | * [https://dev.to/thesaltree/elevator-scheduling-algorithms-fcfs-sstf-scan-and-look-2pae Typy výtahových algoritmů] | ||
| + | * [https://www.kone.cz/studio/tool/#/products Typické konfigurace a technické parametry výtahů] | ||
| + | * [https://digitalcommons.chapman.edu/cgi/viewcontent.cgi?article=1274&context=psychology_articles Rozhodování cestujících a vytížení výtahu v obytné budově] | ||
Latest revision as of 03:48, 16 June 2025
Contents
Simulace vytížení osobních výtahů v budově
Model – simulace ranní špičky v 12patrové residenční budově
Cíl simulace
Cílem simulace je analyzovat chování jednoho výtahu ve 12patrové budově během ranní špičky, kdy obyvatelé postupně opouštějí budovu. Sleduje se průměrná doba čekání, jízdy a celková doba přesunu.
Popis modelu
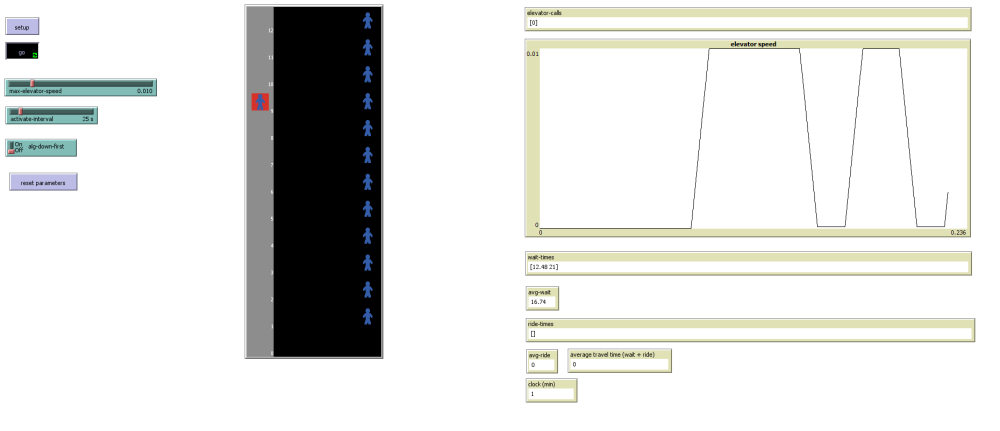
Prostředí:
- 12 podlaží (v rozsahu y = 0 až 12), každý patro výšky 3 metry.
- Rozměr světa:
resize-world 0 4 0 12, velikost patche 50.
Aktéři:
passengers(pasažéři) – modří, každé patro obsahuje 12 pasažérů (celkem 144).elevator(výtah) – jeden červený výtah, začíná v přízemí (y=0).
Vlastnosti pasažéra:
home-floor– domovské patrodestination-floor– cílové patro (v ranní špičce 0)active– označuje aktivované pasažéryin-elevator– zda je pasažér ve výtahuwait-start,wait-stop,ride-start,ride-stop– pro výpočet čekací a jízdní doby
Parametry simulace:
- 100 tick = 3 sekundy → 1 tick = 0.03 s
passenger-speed= 0.02 (pohyb na x-ové ose k výtahu)max-elevator-speed= 0.01 (1 ms)activate-interval= volání každých 25 vteřin – během půl hodiny opustí budovu polovina obyvatel
Algoritmus výtahu
- Dvě strategie:
alg-down-first = false→ klasický algoritmus, jede nahoru/dolů podle požadavkůalg-down-first = true→ výtah nejprve obsluhuje horní patra a sjíždí dolů
- Fronta požadavků:
elevator-calls - Pasažér volá výtah při aktivaci
- Přesun výtahu zahrnuje zrychlení a zpomalení (podle vzdálenosti k cílovému patru)
Výzvy při tvorbě simulace
Mezi největší výzvy patřila funkce move-elevator, kde jsem se rozhodl implementovat plynulý rozjezd a brzdění výtahu. Kvůli tomu bylo nutné vypočítávat vzdálenost potřebnou k zastavení, což vyžadovalo pečlivou synchronizaci s cílovým patrem. Složitým úkolem bylo také správně nastavit chování pasažérů. Narazil jsem například na problém, kdy po nastoupení do výtahu zavolal cílové patro jiný agent než ten, který skutečně nastoupil – trvalo mi několik hodin, než jsem tuto chybu objevil. Další výzvou byl samotný algoritmus volání výtahu, který v této simulaci vychází z algoritmu SCAN – preferuje aktuální směr jízdy a nevrací se, dokud neobslouží všechna volání v daném směru. Bylo obtížné ošetřit hraniční situace, například když volací funkce změnila cíl výtahu, ale funkce move-elevator už dané patro projela. V takovém případě bylo nutné zajistit, aby se ze seznamu volání odstranilo skutečné patro, na kterém výtah zastavil – ne to, které naposledy zavolala funkce call-elevator. Poslední výzvou bylo sledování času a synchronizace simulace, zejména kvůli velkému množství blokujících smyček, které jsem použil pro postupné nastupování/vystupování pasažérů. Celkově je kontinuita simulace velmi složitá a vyžadovala náročné sladění všech částí.
Experimenty a výsledky
Scénář 1: Ranní špička, klasický algoritmus
- Všichni obyvatelé směřují do přízemí (floor = 0)
- Interval aktivace pasažérů: 25 vteřin
- Doba simulace: 30 minut (60 000 ticků)
| Metrika | Hodnota |
|---|---|
| Průměrná doba čekání | 57 s |
| Průměrná doba jízdy | 56 s |
| Průměrná doba přesunu | 110 s |
| Celkový čas simulace | 67 minut |
| Algoritmus | look - down first |
Scénář 2: Algoritmus „nejdříve nahoru“
alg-down-first = true
| Metrika | Hodnota |
|---|---|
| Průměrná doba čekání | 42 s |
| Průměrná doba jízdy | 64 s |
| Průměrná doba přesunu | 107 s |
| Algoritmus | look - up first |
Závěr
Simulace ukázala, že zvolený algoritmus řízení výtahu významně ovlivňuje průběh přepravy cestujících během ranní špičky.
Při použití klasického algoritmu s preferencí směru dolů (look – down first) byla průměrná doba čekání vyšší (57 s), avšak doba jízdy kratší (56 s). Celkový čas přesunu činil 110 sekund. Naopak při algoritmu look – up first (nejprve nahoru) byla doba čekání nižší (42 s), ale cestující strávili více času jízdou (64 s). Celková doba přesunu byla mírně nižší (107 s).
Z výsledků vyplývá, že algoritmus "nejdříve nahoru" přinesl nižší průměrnou dobu čekání i o něco kratší celkový čas přesunu. Tento přístup je tedy v podmínkách simulované ranní špičky mírně efektivnější, přestože cestující urazí delší trasu. Optimalizace směru pohybu výtahu podle očekávaného zatížení pater se tedy jeví jako účinná strategie.
Potenciál a využitelnost simulace
Simulace výtahu má široký potenciál jak pro výukové, tak i praktické účely. Ve výukovém kontextu slouží jako názorný příklad agentově orientovaného modelování, kde lze demonstrovat interakci mezi jednotlivými entitami (pasažéři, výtah) a vliv různých algoritmů řízení na celkovou efektivitu systému. V praxi by podobný model mohl být dále rozšířen a využit například pro optimalizaci výtahových systémů ve vícepodlažních budovách, testování různých řídicích strategií, nebo simulaci zatížení během špiček. S drobnými úpravami by bylo možné model přizpůsobit také pro více výtahů nebo různá pravidla chování cestujících, což by umožnilo reálnější nasazení v oblasti inteligentních budov a facility managementu.