Difference between revisions of "Maze Solving Robot Simulation"
(Created page with "Introduction =Problem definition= =Method= =Model= =Results= =Conclusion= =Code=") |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | One of the typical tasks of the basics of robotics is to build a robot that is able to find his way out of the maze. For this task are used robots that can move along a flat surface, turn and scan the area beneath them at the same time. Maze is represented by a black line on a white surface. The robot moves along the black line, and his aim is to find the end of the maze, which is usually represented by large black rectangle. Task respectively robot is commonly called Line Maze Solving Robot. | |
| − | + | The robot is driven by preloaded algorithm. There are many different algorithms and their modifications. One of the basic algorithms is Left Hand Rule or Right Hand Rule. The algorithm works as follows, the robot prefers left move before moving forward. If this rule cannot be applied, then prefers forward move instead of right move. The algorithm works for all mazes that cannot contain infinite loop, which the robot is not able to solve. | |
| − | = | + | Algorithm Left Hand Rule (Right Hand Rule) is used for example for the initial exploration of the maze (for more information see for example this presentation: https://www.pololu.com/file/0J195/line-maze-algorithm.pdf). Robot passes through the maze and finds its end. During a trip through the maze memorizes all the steps. Stored step data is then robot able to optimize and find the shortest route to the destination. During the second stage the robot can avoid the blind paths and solve the maze using shorter way. As part of this simulation is implemented only the first part - finding way out of the maze. This video shows how the process works: https://www.youtube.com/watch?v=Z0LIO0tEZG4. |
| − | = | + | ==Problem Definition== |
| + | The primary goal is to create an autonomous robot which is Able to find way out of the maze. The robot is programmed and his movements cannot be interfered after he starts. The robot must be driven by a non-trivial algorithm that includes randomly generated numbers (solution for endless loop situations). The robot must be able to find a way out of maze in a finite time. It means he should not get into an endless cycle of no return. | ||
| − | = | + | Secondary objective is to determine what is the difference between a primitive robot and the robot uses a smarter algorithm. Primitive robot is e.g. such a robot who moves only straight forward and if he encounters an obstacle turns left. |
| + | ==Method== | ||
| + | ===Software=== | ||
| + | For simulation is used NetLogo software (2D version). NetLogo was chosen as the most appropriate tool for the simulation because it makes it easy to program the robot's behaviour while allowing visualization of his behaviour. NetLogo also allows to customize the user interface. User can test how a robot algorithm works in real-time and simultaneously monitor other indicators. | ||
| − | = | + | ===Autonomous Robot=== |
| + | Robot is able to move up, down, left and right (viewed from above). He is able to find the way out without any intervention. Robot is able to move in any environment (maze) where exists at least one possible way out. | ||
| − | =Code= | + | ===Intelligent vs Primitive Robot=== |
| + | So called intelligent robot uses an algorithm that allows him to find way out of any maze, where such a path exists. Primitive robot on the other hand, is a robot which uses a very simple set of movement instructions. Primitive robot is e.g. such a robot who moves only straight forward and if he encounters an obstacle turns left. Primitive robot is added to the simulation as a reference. Simulation of intelligent robot are shown in comparison with a primitive robot. | ||
| + | |||
| + | ===Environment (Maze)=== | ||
| + | The environment is adapted to the possibilities of the NetLogo. Environment is represented by the World in NetLogo. The World consists of black, grey and green patches. Black patches represent the path where robot can move. Grey patches represent walls, the robot cannot enter them and finally the green patches are the door out of the maze. | ||
| + | |||
| + | The attached archive contains seven different mazes. Environments vary to demonstrate that the robot is able to avoid infinite loop situations. Maze was created using the Pac-Man Level Editor, which is part of the Library Models in the NetLogo program. Editor has been adapted for the needs of this simulation in accordance to the Creative Commons license. The revised editor served only as a tool for quick creating of a various environments, for the simulation itself is not necessary, therefore the editor is not part of the archive. Size of all seven mazes is 31 x 31 patches. | ||
| + | |||
| + | ==Model== | ||
| + | ===Intelligent Robot=== | ||
| + | As outlined in the introduction above, intelligent robot (red in NetLogo) uses Left Hand Rule algorithm. The algorithm works as follows, a robot prefers left movement before moving forward. If this rule cannot be applied, then prefers forward move instead right move. If any of situations mentioned is not possible, the robot will remain in place and only turn left. Later, when another tick occurs, robot again apply all the previous rules. | ||
| + | |||
| + | Left Hand Rule algorithm is functional for all mazes that cannot contain endless loop. Those situation is not possible to solve by using this algorithm. The purpose of this simulation is to create the robot which is be able to avoid cases with endless loops. For this purpose, algorithm of the robot enriched an element of chance. In one percent of cases when ticks occur robot determine his rotation by a random number generator. For this purpose, is used function for generating random integers. | ||
| + | |||
| + | ===Primitive Robot=== | ||
| + | Primitive robot (blue in NetLogo) uses an algorithm that allows him to movement straight and if he encounters an obstacle turns left. This simple algorithm has the result that the robot is quite often stuck in an endless loop. Primitive robot is created only as a reference to intelligent robot. | ||
| + | |||
| + | ===User Interface=== | ||
| + | The user interface is divided into three areas. The first area Settings (left) is used to select one of the seven mazes, setting robot type, number of robots in a maze and to run a simulation. The second area Visualization (centre) displays the maze and motion of robots in real time. In the third part Statistics (right) are shown statistics of current simulation. | ||
| + | |||
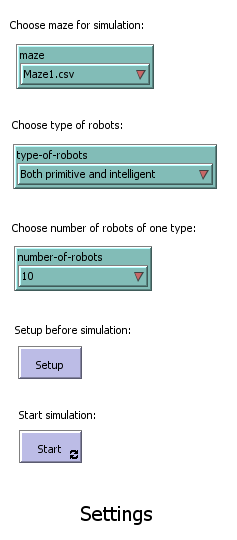
| + | ====Settings==== | ||
| + | Settings consists of five control elements. Three of the five elements are the chooser type and allow to set up one of the seven mazes, setting robot type and number of robots. Mazes are stored in separated files and they need to be stored in the same folder as the file with nlogo extension. There are three combination of robot type. The maze can display separately each of the two types (intelligent and primitive) robots, or both types simultaneously. Selecting the number of robots adjusts how many instances of each type of robot will be displayed in the visualization. In the case that is shown more than one instance of robot, robots are not interact each other. Displaying multiple robots simultaneously serve only for better understanding of the behaviour of intelligent and primitive robot in shorter time. The remaining two buttons is used to apply the selected settings and run the entire simulation. | ||
| + | |||
| + | [[File:Xkrep33 Settings.PNG]] | ||
| + | |||
| + | ====Visualization==== | ||
| + | The middle section shows the maze and selected type and number of robots. | ||
| + | |||
| + | [[File:Xkrep33 Vizualization.PNG]] | ||
| + | |||
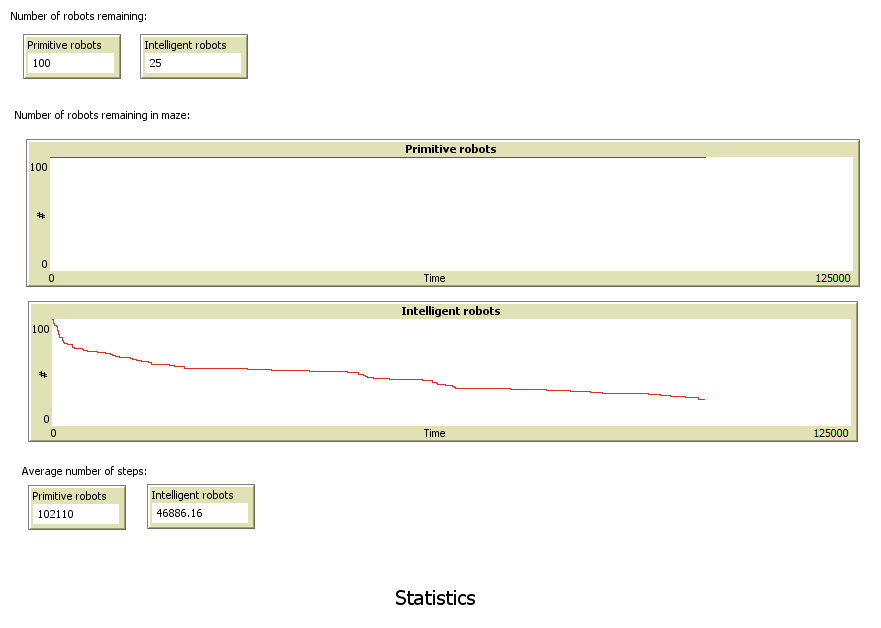
| + | ====Statistics==== | ||
| + | Statistics show three main indicators. The first indicates the number of robots who remain in the maze. This indicator captures all the robots who have not found their way out of the maze yet. The second indicator is a graphical representation of the number of robots remaining in maze during the time elapsed. The third indicator is the average number of steps that robots needed to solve the maze. All indicators are shown, after running a simulation. | ||
| + | |||
| + | [[File:Xkrep33 Statistics.PNG]] | ||
| + | |||
| + | ==Results== | ||
| + | The results are shown in the table. The table contains two figures for both types of robots. Indicator Number of robots remained means how many robots remained in maze when one type of robot solved the maze. If there were more than one robot at the beginning, so it means that all robots of one type solved the maze. Second indicator Average number of steps shows how many steps all robots of one type made on average when they solved the maze. If robots of some type were stuck in infinite loop situation, then numbers are provided in brackets. | ||
| + | |||
| + | There were one thousand of robots of each type at the beginning of each simulation. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Results of seven different mazes simulation | ||
| + | ! style="font-weight: bold;" | | ||
| + | ! colspan="2" style="font-weight: bold;" | Intelligent robots | ||
| + | ! colspan="2" style="font-weight: bold;" | Primitive robots | ||
| + | |- | ||
| + | | style="font-weight: bold;" | Maze No. | ||
| + | | style="font-weight: bold;" | Number of robots remained | ||
| + | | style="font-weight: bold;" | Average number of steps | ||
| + | | style="font-weight: bold;" | Number of robots remained | ||
| + | | style="font-weight: bold;" | Average number of steps | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 1 | ||
| + | | 0 | ||
| + | | 587 | ||
| + | | 1,000 | ||
| + | | (24,804) | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 2 | ||
| + | | 0 | ||
| + | | 528 | ||
| + | | 1,000 | ||
| + | | (4,536) | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 3 | ||
| + | | 0 | ||
| + | | 812 | ||
| + | | 1,000 | ||
| + | | (24,043) | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 4 | ||
| + | | 0 | ||
| + | | 80 | ||
| + | | 1,000 | ||
| + | | (744) | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 5 | ||
| + | | 0 | ||
| + | | 519 | ||
| + | | 1,000 | ||
| + | | (12,626) | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 6 | ||
| + | | 138 | ||
| + | | 160 | ||
| + | | 0 | ||
| + | | 117 | ||
| + | |- | ||
| + | | style="font-weight: bold;" | 7 | ||
| + | | 0 | ||
| + | | 747,177 | ||
| + | | 1,000 | ||
| + | | (70,286) | ||
| + | |} | ||
| + | |||
| + | ==Conclusion== | ||
| + | Simulation was done in all seven mazes. Simulation was always done with a sample of thousand robots of each type (two thousand robots at once). The proposed algorithm of intelligent robots was proved. Robots using a smart algorithm base on Left Hand Rule algorithm and generating random numbers, have always been able to solve the maze. Only in one case (maze No. 6) were primitive robots faster than intelligent one. Even in this case, however, all intelligent robots solved the maze. The primary objective of the simulation, which was to create autonomous robot that does not fall into an infinite loop, was achieved. | ||
| + | |||
| + | The results table clearly shows that primitive algorithm was not very effective. In six of the seven cases, the robots who used this algorithm, get into an endless loop with no return. Only in one case, all primitive robots get out of the maze, and even faster than so called intelligent. It was rather a coincidence, because the maze No. 6 is the only one that could be resolved only by moving straight with combination of left turning in case of an obstacle. | ||
| + | |||
| + | It can be said that the algorithm used for intelligent robots was relatively effective and above all its results were very stable. The only exception was a maze No. 7. Maze No. 7 is essentially infinite space with one exit in the middle. But this maze was also solvable for intelligent robots. | ||
| + | |||
| + | ==Code== | ||
| + | Downloadable archive with nlogo file and seven csv files: | ||
| + | |||
| + | [[File:MazeSolvingRobotSimulation.zip]] | ||
| + | |||
| + | [[User:Xkrep33|Xkrep33]] ([[User talk:Xkrep33|talk]]) 22:17, 16 January 2016 (CET) | ||
Latest revision as of 22:18, 16 January 2016
One of the typical tasks of the basics of robotics is to build a robot that is able to find his way out of the maze. For this task are used robots that can move along a flat surface, turn and scan the area beneath them at the same time. Maze is represented by a black line on a white surface. The robot moves along the black line, and his aim is to find the end of the maze, which is usually represented by large black rectangle. Task respectively robot is commonly called Line Maze Solving Robot.
The robot is driven by preloaded algorithm. There are many different algorithms and their modifications. One of the basic algorithms is Left Hand Rule or Right Hand Rule. The algorithm works as follows, the robot prefers left move before moving forward. If this rule cannot be applied, then prefers forward move instead of right move. The algorithm works for all mazes that cannot contain infinite loop, which the robot is not able to solve.
Algorithm Left Hand Rule (Right Hand Rule) is used for example for the initial exploration of the maze (for more information see for example this presentation: https://www.pololu.com/file/0J195/line-maze-algorithm.pdf). Robot passes through the maze and finds its end. During a trip through the maze memorizes all the steps. Stored step data is then robot able to optimize and find the shortest route to the destination. During the second stage the robot can avoid the blind paths and solve the maze using shorter way. As part of this simulation is implemented only the first part - finding way out of the maze. This video shows how the process works: https://www.youtube.com/watch?v=Z0LIO0tEZG4.
Contents
Problem Definition
The primary goal is to create an autonomous robot which is Able to find way out of the maze. The robot is programmed and his movements cannot be interfered after he starts. The robot must be driven by a non-trivial algorithm that includes randomly generated numbers (solution for endless loop situations). The robot must be able to find a way out of maze in a finite time. It means he should not get into an endless cycle of no return.
Secondary objective is to determine what is the difference between a primitive robot and the robot uses a smarter algorithm. Primitive robot is e.g. such a robot who moves only straight forward and if he encounters an obstacle turns left.
Method
Software
For simulation is used NetLogo software (2D version). NetLogo was chosen as the most appropriate tool for the simulation because it makes it easy to program the robot's behaviour while allowing visualization of his behaviour. NetLogo also allows to customize the user interface. User can test how a robot algorithm works in real-time and simultaneously monitor other indicators.
Autonomous Robot
Robot is able to move up, down, left and right (viewed from above). He is able to find the way out without any intervention. Robot is able to move in any environment (maze) where exists at least one possible way out.
Intelligent vs Primitive Robot
So called intelligent robot uses an algorithm that allows him to find way out of any maze, where such a path exists. Primitive robot on the other hand, is a robot which uses a very simple set of movement instructions. Primitive robot is e.g. such a robot who moves only straight forward and if he encounters an obstacle turns left. Primitive robot is added to the simulation as a reference. Simulation of intelligent robot are shown in comparison with a primitive robot.
Environment (Maze)
The environment is adapted to the possibilities of the NetLogo. Environment is represented by the World in NetLogo. The World consists of black, grey and green patches. Black patches represent the path where robot can move. Grey patches represent walls, the robot cannot enter them and finally the green patches are the door out of the maze.
The attached archive contains seven different mazes. Environments vary to demonstrate that the robot is able to avoid infinite loop situations. Maze was created using the Pac-Man Level Editor, which is part of the Library Models in the NetLogo program. Editor has been adapted for the needs of this simulation in accordance to the Creative Commons license. The revised editor served only as a tool for quick creating of a various environments, for the simulation itself is not necessary, therefore the editor is not part of the archive. Size of all seven mazes is 31 x 31 patches.
Model
Intelligent Robot
As outlined in the introduction above, intelligent robot (red in NetLogo) uses Left Hand Rule algorithm. The algorithm works as follows, a robot prefers left movement before moving forward. If this rule cannot be applied, then prefers forward move instead right move. If any of situations mentioned is not possible, the robot will remain in place and only turn left. Later, when another tick occurs, robot again apply all the previous rules.
Left Hand Rule algorithm is functional for all mazes that cannot contain endless loop. Those situation is not possible to solve by using this algorithm. The purpose of this simulation is to create the robot which is be able to avoid cases with endless loops. For this purpose, algorithm of the robot enriched an element of chance. In one percent of cases when ticks occur robot determine his rotation by a random number generator. For this purpose, is used function for generating random integers.
Primitive Robot
Primitive robot (blue in NetLogo) uses an algorithm that allows him to movement straight and if he encounters an obstacle turns left. This simple algorithm has the result that the robot is quite often stuck in an endless loop. Primitive robot is created only as a reference to intelligent robot.
User Interface
The user interface is divided into three areas. The first area Settings (left) is used to select one of the seven mazes, setting robot type, number of robots in a maze and to run a simulation. The second area Visualization (centre) displays the maze and motion of robots in real time. In the third part Statistics (right) are shown statistics of current simulation.
Settings
Settings consists of five control elements. Three of the five elements are the chooser type and allow to set up one of the seven mazes, setting robot type and number of robots. Mazes are stored in separated files and they need to be stored in the same folder as the file with nlogo extension. There are three combination of robot type. The maze can display separately each of the two types (intelligent and primitive) robots, or both types simultaneously. Selecting the number of robots adjusts how many instances of each type of robot will be displayed in the visualization. In the case that is shown more than one instance of robot, robots are not interact each other. Displaying multiple robots simultaneously serve only for better understanding of the behaviour of intelligent and primitive robot in shorter time. The remaining two buttons is used to apply the selected settings and run the entire simulation.
Visualization
The middle section shows the maze and selected type and number of robots.
Statistics
Statistics show three main indicators. The first indicates the number of robots who remain in the maze. This indicator captures all the robots who have not found their way out of the maze yet. The second indicator is a graphical representation of the number of robots remaining in maze during the time elapsed. The third indicator is the average number of steps that robots needed to solve the maze. All indicators are shown, after running a simulation.
Results
The results are shown in the table. The table contains two figures for both types of robots. Indicator Number of robots remained means how many robots remained in maze when one type of robot solved the maze. If there were more than one robot at the beginning, so it means that all robots of one type solved the maze. Second indicator Average number of steps shows how many steps all robots of one type made on average when they solved the maze. If robots of some type were stuck in infinite loop situation, then numbers are provided in brackets.
There were one thousand of robots of each type at the beginning of each simulation.
| Intelligent robots | Primitive robots | |||
|---|---|---|---|---|
| Maze No. | Number of robots remained | Average number of steps | Number of robots remained | Average number of steps |
| 1 | 0 | 587 | 1,000 | (24,804) |
| 2 | 0 | 528 | 1,000 | (4,536) |
| 3 | 0 | 812 | 1,000 | (24,043) |
| 4 | 0 | 80 | 1,000 | (744) |
| 5 | 0 | 519 | 1,000 | (12,626) |
| 6 | 138 | 160 | 0 | 117 |
| 7 | 0 | 747,177 | 1,000 | (70,286) |
Conclusion
Simulation was done in all seven mazes. Simulation was always done with a sample of thousand robots of each type (two thousand robots at once). The proposed algorithm of intelligent robots was proved. Robots using a smart algorithm base on Left Hand Rule algorithm and generating random numbers, have always been able to solve the maze. Only in one case (maze No. 6) were primitive robots faster than intelligent one. Even in this case, however, all intelligent robots solved the maze. The primary objective of the simulation, which was to create autonomous robot that does not fall into an infinite loop, was achieved.
The results table clearly shows that primitive algorithm was not very effective. In six of the seven cases, the robots who used this algorithm, get into an endless loop with no return. Only in one case, all primitive robots get out of the maze, and even faster than so called intelligent. It was rather a coincidence, because the maze No. 6 is the only one that could be resolved only by moving straight with combination of left turning in case of an obstacle.
It can be said that the algorithm used for intelligent robots was relatively effective and above all its results were very stable. The only exception was a maze No. 7. Maze No. 7 is essentially infinite space with one exit in the middle. But this maze was also solvable for intelligent robots.
Code
Downloadable archive with nlogo file and seven csv files: