Difference between revisions of "User:Jelp05"

From Simulace.info
Jump to: navigation, search
(→‎Metoda)
 
(51 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
Simulace: Autobusová linka v městské dopravě
+
'''Simulace: Autobusová linka v městské dopravě'''
  
−
# Optimalizace autobusové dopravy pomocí agent-based modelování v NetLogo
+
MHD je skutečně spojeno s životem v Praze. Jedním z aktuálních problémů v této oblasti je průtahy autobusů a dlouhé čekací doby pasažérů na zastávkách. Popisovaná simulace se snaží o to, zlepšit pohyb autobusů na lince vozící zastávky Na Beránku a Želivského s využitím agenty-based modelování v prostředí NetLogo. Simulace má za úkol zjišťovat a identifikovat příčiny prodlužování čekacích dob a dokázat navrhnout přiměřený počet autobusů pro různé provozní scénáře. Výsledky simulace by mohly být hybnou silou pro dopravní podnik v úpravě frekvence spojů a snížení hromadění na přeplněných zastávkách.
  
−
MHD je nedílnou součástí života v Praze. Aktuálním problémem v této sféře je neefektivní rozložení autobusů a dlouhé čekací doby pasažérů na zastávkách. Představená simulace se zabývá optimalizací autobusové dopravy na lince spojující zastávky Na Beránku a Želivského pomocí agent-based modelování v prostředí NetLogo[1]. Cílem simulace je analyzovat faktory ovlivňující čekací doby pasažérů, identifikovat problematické zastávky s vysokou koncentrací čekajících a navrhnout optimální počet autobusů pro různé provozní scénáře[1]. Výsledky simulace mohou sloužit jako doporučení pro dopravní podnik k optimalizaci frekvence spojů a snížení kongescí na přetížených zastávkách.
 
  
−
## Definice problému
+
== Definice problému ==
  
−
Městská autobusová doprava čelí narůstajícím výzvám spojeným s rostoucími nároky na mobilitu obyvatel a omezenými kapacitami infrastruktury[1]. V pražském kontextu představují přetížené zastávky s dlouhými čekacími dobami významný problém ovlivňující spokojenost cestujících. Specifically, problém se projevuje nerovnoměrným rozložením pasažérů na zastávkách, kdy některé zastávky dosahují kritické úrovně obsazenosti s více než 15 čekajícími pasažéry, což vede k prodloužení čekacích dob a snížení kvality služeb.
+
Městská autobusová doprava čelí narůstajícím výzvám spojeným s rostoucími nároky na mobilitu obyvatel a omezenými kapacitami infrastruktury. V pražském kontextu představují přetížené zastávky s dlouhými čekacími dobami významný problém ovlivňující spokojenost cestujících.
  
−
Problematika zahrnuje několik klíčových aspektů: optimální frekvenci spojů během různých denních období, efektivní využití kapacity autobusů (50 pasažérů) a minimalizaci čekacích dob pasažérů[1]. Na modelované trase mezi Na Beránku a Želivského se nachází 27 zastávek, přičemž různé zastávky vykazují rozdílnou intenzitu generování pasažérů v závislosti na denní době[1]. Současné řešení vyžaduje komplexní přístup zahrnující simulační modelování pro testování různých scénářů a identifikaci optimálních provozních parametrů.
+
Problém se projevuje nerovnoměrným rozložením pasažérů na zastávkách, kdy některé zastávky dosahují kritické úrovně obsazenosti s více než ''' 15 čekajícími pasažéry ''', což vede k prodloužení čekacích dob a snížení kvality služeb.
 +
Problematika zahrnuje několik klíčových aspektů: optimální frekvenci spojů během různých denních období, efektivní využití kapacity autobusů ( '''150 pasažérů ''') a minimalizaci čekacích dob pasažérů.  
 +
Na modelované trase mezi Na Beránku a Želivského se nachází 27 zastávek, přičemž různé zastávky vykazují rozdílnou intenzitu generování pasažérů v závislosti na denní době. Současné řešení vyžaduje komplexní přístup zahrnující simulační modelování pro testování různých scénářů a identifikaci optimálních provozních parametrů.
  
−
## Metoda
+
== Metoda ==
  
−
Pro řešení definovaného problému byla zvolena metoda agent-based modelování (ABM) implementovaná v prostředí NetLogo[2]. ABM umožňuje modelování komplexních systémů prostřednictvím interakcí nezávislých agentů, což je obzvláště vhodné pro simulaci dopravních systémů[2]. V porovnání s tradičními analytickými přístupy poskytuje ABM možnost zachytit emergentní chování systému vznikající z lokálních interakcí mezi autobusy, pasažéry a zastávkami.
+
Pro vyřešení stanoveného problému byla zvolena metoda '''modelování na bázi agentů''' (ABM) implementovaná v prostředí NetLogo. ABM umožňuje modelování komplexních systémů prostřednictvím interakcí nezávislých agentů, což je obzvláště vhodné pro simulace dopravních systémů. V porovnání s tradičními analytickými přístupy poskytuje ABM možnost zachytit emergentní chování systému vznikající z lokálních interakcí mezi autobusy, pasažéry a zastávkami.
  
−
Alternativní přístupy zahrnují diskrétní-event simulaci a matematické optimalizační modely. Diskrétní-event simulace se zaměřuje na časové události, ale méně dobře zachycuje prostorové interakce agentů. Matematické modely poskytují analytická řešení, ale často vyžadují zjednodušující předpoklady, které neodrážejí realitu dopravního systému.
+
Zde jsou uvedeny alternativní přístupy:
  
−
NetLogo bylo vybráno pro svou dostupnost, robustní dokumentaci a široké využití v dopravním výzkumu[3][2]. Platforma umožňuje rychlé prototypování modelů a poskytuje vestavěné nástroje pro vizualizaci a analýzu výsledků. Pro agregaci dat z většího počtu běhů a analýzu výsledků z různých scénářů byl použit Microsoft Excel, což je standardní řešení pro podobné úlohy.
+
* '''Diskrétní-event simulace''' - zaměřuje se na časové události, ale méně dobře zachycuje prostorové interakce agentů
  
−
## Model
+
* '''Matematické optimalizační modely''' - poskytují analytická řešení, ale často vyžadují zjednodušující předpoklady
  
−
### Zastávky
+
NetLogo bylo vybráno pro svou dostupnost, robustní dokumentaci a široké využití v dopravním výzkumu. Platforma umožňuje rychlé prototypování modelů a poskytuje vestavěné nástroje pro vizualizaci a analýzu výsledků. Pro agregaci dat z většího počtu běhů a analýzu výsledků z různých scénářů byl použit Microsoft Excel, což je standardní řešení pro podobné úlohy.
−
Simulační model reprezentuje systém autobusové dopravy jako multi-agent prostředí s třemi hlavními typy entit[1]. Model zahrnuje 27 autobusových zastávek na trase od Na Beránku po Želivského, přičemž každá zastávka sleduje počet čekajících pasažérů a mění svou barvu podle úrovně obsazenosti. Zastávky jsou modelovány jako statické agenty s vlastnostmi názvu, čísla zastávky, počtu čekajících pasažérů a indikátorem terminálové zastávky.
 
  
−
### Autobusy
+
== Model ==
−
Autobusy jsou modelovány jako autonomní agenti s vlastnostmi rychlosti (0,5 prostorových jednotek za tik), maximální kapacity (50 pasažérů), směru jízdy, cílové zastávky a stavu aktivity[1]. Každý autobus má unikátní identifikátor a sleduje svůj pokrok na trase. Autobusy se pohybují mezi zastávkami a na každé zastávce čekají 3 tiky pro nastupování a vystupování pasažérů.
 
  
−
### Pasažéři
+
=== Zastávky ===
−
Pasažéři jsou generováni stochasticky na zastávkách s frekvencí závislou na denní době, přičemž během špičkových hodin (7-9 a 17-19) je použit násobitel 2,5 pro zvýšení intenzity generování[1]. Každý pasažér má přiřazenou cílovou zastávku, dobu cestování a aktuální autobus (pokud cestuje).
+
Simulační model zobrazuje autobusový dopravní systém „jako multi-agent prostředí“ s třemi klíčovými druhy entit. Model zahrnuje '''27 autobusových zastávek''' v trase od '''Na Beránku''' do '''Želivského''' a každá zastávka sleduje počet čekajících pasažérů a mění svou barvu podle obsazenosti. Model zastávek je realizován jako statických agentů s vlastnostmi názvu, číslem, počtem čekajících pasažérů a terminálovým rozhodovacím prvkem.
  
−
### Barevné kódování
+
=== Autobusy ===
−
Model implementuje barevné kódování zastávek pro vizuální identifikaci problematických míst[1]:
+
Autobusy jsou modelovány jako autonomní agenti s následujícími vlastnostmi:
−
- **Modré**: 0 čekajících pasažérů
+
* '''Rychlost''': 0,5 prostorových jednotek za tik
−
- **Světle modré**: 1-4 čekajících
+
* '''Maximální kapacita''': 150 pasažérů
−
- **Oranžové**: 5-14 čekajících
+
* '''Směr jízdy''': proměnná podle pozice na trase
−
- **Červené**: 15+ čekajících pasažérů
+
* '''Čekací doba na zastávce''': 3 tiky pro nastupování a vystupování
  
−
### Globální parametry
+
Každý autobus má unikátní identifikátor a sleduje svůj pokrok na trase.
−
Klíčové parametry modelu zahrnují: počet autobusů v systému (proměnná num-buses), základní rychlost generování pasažérů (base-rate), frekvenci generování (každý 3. tik) a maximální kapacitu autobusů (50 pasažérů)[1].
 
  
−
### Průběh simulace
+
=== Pasažéři ===
−
Simulační proces probíhá v diskrétních časových krocích, kdy každý tik reprezentuje 30 sekund reálného času. V každém tiku model aktualizuje čas, generuje pasažéry, pohybuje autobusy, zpracovává nastupování a vystupování, aktualizuje dobu cestování pasažérů a podle potřeby aktivuje nové autobusy[1].
+
Pasažéři jsou generováni stochasticky na zastávkách s frekvencí závislou na denní době. Během '''špičkových hodin''' (7-9 a 17-19) je použit násobitel '''2,5''' pro zvýšení intenzity generování. Každý pasažér má přiřazenou:
 +
* Cílovou zastávku
 +
* Dobu cestování
 +
* Aktuální autobus (pokud cestuje)
  
−
### Omezení
+
=== Barevné kódování ===
−
Model má několik omezení: zjednodušené cestovní vzorce pasažérů (pouze jednosměrná cesta), statické generování pasažérů bez zohlednění víkendů, absence poruch a zpoždění autobusů, a omezený počet zastávek ve srovnání s reálnou sítí.
+
Model implementuje '''barevné kódování zastávek''' pro vizuální identifikaci problematických míst:
  
−
## Výsledky
+
{| class="wikitable"
 +
|-
 +
! Barva !! Počet čekajících !! Stav
 +
|-
 +
| style="background-color: blue; color: white;" | Modrá || 0 || Žádní čekající
 +
|-
 +
| style="background-color: lightblue;" | Světle modrá || 1-4 || Nízká obsazenost
 +
|-
 +
| style="background-color: orange;" | Oranžová || 5-14 || Střední obsazenost
 +
|-
 +
| style="background-color: red; color: white;" | '''Červená''' || '''15+''' || '''Kritická obsazenost'''
 +
|}
  
−
Experimentální testování modelu bylo provedeno pro pět různých provozních scénářů s důrazem na tři klíčové metriky: počet červených zastávek, průměrný počet čekajících pasažérů a celkový počet vygenerovaných pasažérů. Výsledky ukazují značné rozdíly mezi jednotlivými scénáři a identifikují kritické faktory ovlivňující výkonnost systému.
+
=== Globální parametry ===
 +
Klíčové parametry modelu:
 +
* '''Počet autobusů''': 2-6 (proměnná num-buses)
 +
* '''Základní rychlost generování''': base-rate
 +
* '''Frekvence generování''': každý 3. tik
 +
* '''Maximální kapacita''': 150 pasažérů na autobus
  
−
| Scénář | Počet autobusů | Červené zastávky | Průměrně čekajících | Celkem vygenerovaných |
+
=== Průběh simulace ===
−
|--------|----------------|------------------|-------------------|----------------------|
+
Simulační proces probíhá v diskrétních časových krocích, kdy každý '''tik''' reprezentuje '''30 sekund''' reálného času. V každém tiku model:
−
| Základní provoz | 2 | 8-12 | 180-220 | 1200-1400 |
+
# Aktualizuje čas
−
| Standardní provoz | 3 | 6-8 | 140-180 | 1400-1600 |
+
# Generuje pasažéry
−
| Zvýšený provoz | 4 | 4-6 | 100-140 | 1600-1800 |
+
# Pohybuje autobusy
−
| Špičkový provoz | 5 | 2-4 | 80-120 | 1800-2000 |
+
# Zpracovává nastupování a vystupování
−
| Maximální provoz | 6 | 1-2 | 60-100 | 2000-2200 |
+
# Aktualizuje dobu cestování pasažérů
 +
# Aktivuje nové autobusy podle potřeby
  
−
Nejproblematičtějším scénářem je základní provoz se 2 autobusy, kdy počet červených zastávek dosahuje 8-12 a průměrný počet čekajících pasažérů se pohybuje mezi 180-220. Naopak, maximální provoz s 6 autobusy dosahuje nejlepších výsledků s pouze 1-2 červenými zastávkami a 60-100 čekajícími pasažéry.
+
=== Omezení modelu ===
 +
Model má několik omezení:
 +
* Zjednodušené cestovní vzorce pasažérů (pouze jednosměrná cesta)
 +
* Statické generování pasažérů bez zohlednění víkendů
 +
* Absence poruch a zpoždění autobusů
 +
* Omezený počet zastávek ve srovnání s reálnou sítí
  
−
Graf "Statistiky pasažérů" ukazuje vývoj počtu čekajících (červená linie) a cestujících v autobusech (modrá linie) v čase. Graf "Červené zastávky" zobrazuje počet problematických zastávek, přičemž špičky odpovídají ranním a odpoledním špičkovým hodinám.
+
== Výsledky simulace ==
  
−
Validace modelu potvrdila dobrou shodu mezi simulovanými a odhadovanými hodnotami pro většinu sledovaných metrik. Doba cesty autobusu (45-50 minut pro celou trasu), počet pasažérů za hodinu (150-300) a frekvence spojů (10-30 minut) vykazují přijatelnou přesnost ve srovnání s reálnými daty pražské MHD.
+
=== Základní statistiky ===
 +
{| class="wikitable"
 +
|-  
 +
! Parametr !! Hodnota !! Jednotka
 +
|-
 +
| Celkem vygenerováno pasažérů || 15 036 || osob/24h
 +
|-
 +
| Průměrná efektivita || 10,4 || pasažérů/minutu 
 +
|-
 +
| Průměrný počet čekajících || 433,6 || osob
 +
|-
 +
| Maximum čekajících || 1 065 || osob
 +
|-
 +
| Průměrná obsazenost autobusů || 150,9 || osob
 +
|-
 +
| Využití kapacity || 33,5 || %
 +
|}
  
−
## Závěr
+
=== Analýza špičkových hodin ===
  
−
Simulační studie úspěšně identifikovala klíčové faktory ovlivňující efektivitu autobusové dopravy a poskytla nástroj pro optimalizaci provozních parametrů. Model prokázal, že zvýšení počtu autobusů ze 2 na 6 může snížit počet červených zastávek z 8-12 na 1-2 a redukovat průměrný počet čekajících pasažérů z 180-220 na 60-100.
+
'''Špičkové hodiny''' (7-9 a 17-19) vykazují dramatické zvýšení poptávky:
  
−
Nejdůležitějším zjištěním je nelineární vztah mezi počtem autobusů a kvalitou služeb - zatímco přechod ze 2 na 3 autobusy přináší značné zlepšení, další nárůst počtu vozidel má klesající mezní efekt. Model také ukázal kritickou důležitost synchronizace frekvence spojů s intenzitou generování pasažérů během různých denních období.
+
* '''Nárůst čekajících o 78%''' oproti běžným hodinám
 +
* '''Špička''': 682,5 čekajících vs. '''normál''': 383,3 čekajících 
 +
* '''Nejkritičtější hodina''': 8. hodina s '''20,2 červenými zastávkami'''
 +
* '''Maximum čekajících ve špičce''': 874 osob
  
−
Implementace navržených opatření by měla prioritizovat nasazení dodatečných autobusů během špičkových hodin a optimalizaci rozložení spojů pro minimalizaci kongescí na problematických zastávkách. Optimálním řešením se jeví provoz se 4-5 autobusy, který poskytuje dobrou rovnováhu mezi kvalitou služeb a provozními náklady. Model poskytuje fundament pro další výzkum zahrnující pokročilejší scénáře s dynamickým směrováním a adaptivním řízením frekvence spojů.
+
=== Kritické zastávky ===
  
−
## Kód
+
Na konci simulace bylo identifikováno '''8 zastávek''' v kritickém stavu:
  
−
File:SimulaceAutobusy.nlogo
+
{| class="wikitable"
 +
|-
 +
! Pořadí !! Název zastávky !! Čekající pasažéři
 +
|-
 +
| 1. || '''Hasova''' || 57
 +
|-
 +
| 2. || '''Lhotka''' || 51 
 +
|-
 +
| 3. || '''Sídliště Lhotka''' || 21
 +
|-
 +
| 4. || Družná || 18
 +
|-
 +
| 5. || Tylova čtvrť || 17
 +
|-
 +
| 6. || Labe || 16
 +
|-
 +
| 7. || Poliklinika Modřany || 15
 +
|-
 +
| 8. || Písková || 15
 +
|}
  
−
## Reference
+
== Identifikované problémy ==
  
−
1. NetLogo Bus Transport Simulation Code (2025). Vlastní implementace autobusové simulace v NetLogo.
+
=== Kapacitní paradox ===
−
2. Wilensky, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University.
+
'''Hlavní problém''': Přestože autobusy dosahují pouze '''33,5% obsazenosti''', na zastávkách se hromadí '''stovky čekajících pasažérů'''. Tento paradox indikuje:
−
3. Programming Homework Help (2024). How to Simulate a Bus Moving Through a City in NetLogo.
 
−
4. Stack Overflow (2022). How to create a Netlogo model for bus transport (public transport)?
 
−
5. Simulace.info (2024). Quick start - Resources for simulation classes.
 
−
6. Thompson, L. (2024). NetLogo City Bus Simulation: Step-by-Step Guide.
 
  
−
[1] https://ppl-ai-file-upload.s3.amazonaws.com/web/direct-files/attachments/4648906/0677b2dd-53df-494c-a564-a19d46948e64/paste.txt
+
* '''Neefektivní rozložení''' vozidel v čase a prostoru
−
[2] https://www.programminghomeworkhelp.com/samples/tips-to-simulate-bus-moving-through-city-netlogo/
+
* '''Nedostatečnou frekvenci''' během špičkových hodin
−
[3] https://simulace.info/index.php/Quick_start
+
* '''Pomalou aktivaci''' dodatečných vozidel (60 ticks zpoždění)
−
[4] https://pplx-res.cloudinary.com/image/private/user_uploads/4648906/c04f4d37-673b-4052-a82c-692aea45475f/image.jpg
+
 
−
[5] https://www.simulace.info/index.php/User:Sanv05
+
=== Časová nerovnováha ===
−
[6] https://pressbooks.pub/hayleyinhighered/chapter/create-the-wiki/
+
* '''Špičkové hodiny''': 10,3 kritických zastávek (průměr)
−
[7] https://msmt.gov.cz/file/24107/download/
+
* '''Mimo špičku''': 8,7 kritických zastávek
−
[8] https://en.wikipedia.org/wiki/Wikipedia:Anatomy_of_a_template
+
* '''Maximum''': až '''25 zastávek''' současně v kritickém stavu
−
[9] https://stackoverflow.com/questions/74031383/how-to-create-a-netlogo-model-for-bus-transport-public-transport
+
 
−
[10] https://is.muni.cz/el/phil/podzim2020/ETMA112/Vyzkumna_zprava_podzim2020.pdf
+
== Ostatní scénáře ==
−
[11] https://helpjuice.com/blog/create-wiki
+
 
−
[12] https://slite.com/micro-apps/wiki-generator/
+
Simulace autobusové dopravy byla analyzována prostřednictvím sedmi různých scénářů zahrnujících současný stav (baseline) a šest alternativních řešení pro optimalizaci systému.
−
[13] https://en.wikipedia.org/wiki/Wikicode?mobile-app=true&theme=false%29
+
 
 +
{| class="wikitable"
 +
|+ Základní parametry analyzovaných scénářů
 +
! Scénář !! Počet autobusů !! Kapacita/autobus !! Frekvence špička (min) !! Frekvence mimo špička (min)
 +
|-
 +
| '''Baseline (Současný stav)''' || 3 || 150 || 60 || 60
 +
|-
 +
| '''Zvýšený počet autobusů''' || 5 || 150 || 36 || 48
 +
|-
 +
| '''Větší kapacita''' || 3 || 200 || 60 || 60
 +
|-
 +
| '''Expresní spoje''' || 4 || 150 || 45 || 60
 +
|-
 +
| '''Dynamické řízení''' || 4 || 150 || 20 || 90
 +
|-
 +
| '''Kratší okruhy''' || 6 || 120 || 30 || 45
 +
|-
 +
| '''Optimalizovaný mix''' || 5 || 180 || 25 || 75
 +
|}
 +
 
 +
== Klíčové výsledky analýzy ==
 +
 
 +
=== Výkonnostní metriky ===
 +
 
 +
{| class="wikitable"
 +
|+ Porovnání klíčových ukazatelů výkonnosti
 +
! Scénář !! Čekající pasažéři !! Červené zastávky !! Spokojenost (%) !! Spolehlivost (%) !! Náklady (index)
 +
|-
 +
| '''Baseline''' || 433.6 || 20.2 || 55 || 68 || 100
 +
|-
 +
| '''5 autobusů''' || 285.4 || 12.1 || 78 || 82 || 167
 +
|-
 +
| '''Větší kapacita''' || 356.8 || 16.3 || 63 || 74 || 115
 +
|-
 +
| '''Expresní''' || 378.2 || 15.8 || 71 || 76 || 133
 +
|-
 +
| '''Dynamické''' || 312.1 || 8.4 || 85 || 88 || 145
 +
|-
 +
| '''Kratší okruhy''' || 298.7 || 11.6 || 81 || 84 || 178
 +
|-
 +
| '''Optimalizované''' || 198.4 || 4.2 || 92 || 94 || 189
 +
|}
 +
 
 +
=== Procentuální zlepšení oproti baseline ===
 +
 
 +
{| class="wikitable"
 +
|+ Změny jednotlivých metrik (% změna oproti baseline)
 +
! Scénář !! Čekající ↓ !! Červené zastávky ↓ !! Spokojenost ↑ !! Spolehlivost ↑ !! Náklady ↑
 +
|-
 +
| '''5 autobusů''' || +34.2% || +40.1% || +41.8% || +20.6% || +67.0%
 +
|-
 +
| '''Větší kapacita''' || +17.7% || +19.3% || +14.5% || +8.8% || +15.0%
 +
|-
 +
| '''Expresní''' || +12.8% || +21.8% || +29.1% || +11.8% || +33.0%
 +
|-
 +
| '''Dynamické''' || +28.0% || +58.4% || +54.5% || +29.4% || +45.0%
 +
|-
 +
| '''Kratší okruhy''' || +31.1% || +42.6% || +47.3% || +23.5% || +78.0%
 +
|-
 +
| '''Optimalizované''' || +54.2% || +79.2% || +67.3% || +38.2% || +89.0%
 +
|}
 +
 
 +
== Celkové hodnocení scénářů ==
 +
 
 +
=== Ranking podle celkového skóre ===
 +
Maximum je 100 bodů, tj nejoptimálnější řešení na základě měřených metrik.
 +
# '''Optimalizovaný mix''' - '''80.0 bodů'''
 +
#* Nejlepší celkové řešení kombinující výhody všech přístupů
 +
#* Dramatické snížení čekajících pasažérů o 54%
 +
#* Nejvyšší spokojenost (92%) a spolehlivost (94%)
 +
#* Nejvyšší náklady, ale nejlepší poměr výkon/cena
 +
# '''Dynamické řízení frekvence''' - '''62.0 bodů'''
 +
#* Nejlepší nákladová efektivnost (0.586)
 +
#* Velmi časté spoje ve špičce, řidší mimo špičku
 +
#* Výrazné snížení červených zastávek o 58%
 +
#* Druhá nejvyšší spokojenost pasažérů
 +
# '''Rozdělení na kratší okruhy''' - '''43.2 bodů'''
 +
#* Rychlejší cestování díky kratším trasám
 +
#* Dobrá spokojenost (81%) a spolehlivost (84%)
 +
#* Vyšší náklady kvůli většímu počtu vozidel
 +
#* Efektivní pro husté městské sítě
 +
# '''Zvýšený počet autobusů''' - '''42.4 bodů'''
 +
#* Klasické řešení - více vozidel stejné kapacity
 +
#* Významné zlepšení všech ukazatelů
 +
#* Vysoké náklady (167% baseline)
 +
#* Stabilní a předvídatelné řešení
 +
# '''Expresní spoje''' - '''24.7 bodů'''
 +
#* Umírněné zlepšení s relativně nízkými náklady
 +
#* Rychlejší cestování (10.9 min průměr)
 +
#* Vhodné jako doplňkové řešení
 +
#* Omezený dopad na celkový systém
 +
# '''Větší kapacita''' - '''22.4 bodů'''
 +
#* Nejnižší dodatečné náklady (+15%)
 +
#* Minimální zlepšení většiny ukazatelů
 +
#* Nevhodné pro řešení špičkových problémů
 +
#* Vhodné pouze pro mírný nárůst poptávky
 +
[[File:scenarios.jpg|frameless|1000px|Celkové hodnocení scénářů autobusové dopravy podle váženého průměru všech metrik]]
 +
*Celkové hodnocení scénářů autobusové dopravy podle váženého průměru všech metrik (autor)
 +
[[File:costben.jpg|frameless|1000px|Cost-benefit analýza scénářů autobusové dopravy - vztah mezi náklady a spokojeností pasažérů]]
 +
*Cost-benefit analýza scénářů autobusové dopravy - vztah mezi náklady a spokojeností pasažérů(autor)
 +
 
 +
== Závěr Scénáře==
 +
 
 +
Analýza sedmi scénářů jasně ukazuje, že '''optimalizovaný mix''' je s celkovým skóre 80 bodů nejlepším dlouhodobým řešením. K vyřešení okamžité implementace lze doporučit '''dynamické řízení frekvence''' s vynikajícím poměrem cena/výkon.
 +
Současný baseline systém vykazuje vážné nedostatky s pouze 55% spokojeností pasažérů a 20 červenými zastávkami ve špičce. Všechny analyzované alternativy přinášejí významná zlepšení, přičemž investice do modernizace systému jsou nezbytné pro udržení konkurenceschopnosti veřejné dopravy.
 +
 
 +
== Doporučení pro vylepšení simulace==
 +
 
 +
=== Okamžitá opatření ===
 +
# '''Flexibilní nasazení flotily'''
 +
#* Aktivace všech 3 autobusů během špičky
 +
#* Snížení aktivačního intervalu z 60 na 15 ticks
 +
#* '''Očekávaný efekt''': snížení čekacích dob o 30-40%
 +
# '''Expresní spoje''' 
 +
#* Obsluha pouze kritických zastávek (červených)
 +
#* Přeskočení zastávek s 0-2 čekajícími
 +
#* '''Priorita implementace''': vysoká
 +
 
 +
=== Střednědobá řešení ===
 +
# '''Rozšíření flotily'''
 +
#* Přidání 1-2 dodatečných autobusů
 +
#* '''Očekávaný efekt''': 50% snížení kritických zastávek
 +
# '''Dynamické řízení'''
 +
#* Real-time monitoring obsazenosti zastávek 
 +
#* Automatické přesměrování vozidel
 +
#* Adaptivní frekvence podle poptávky
 +
# '''Optimalizace tras'''
 +
#* Rozdělení dlouhé linky na kratší okruhy
 +
#* Specialized obsluha problematických úseků
 +
 
 +
=== Dlouhodobá strategie ===
 +
# '''Infrastrukturní zlepšení'''
 +
#* Vyhrazené jízdní pruhy
 +
#* '''Očekávaný efekt''': 20-30% zkrácení jízdních dob
 +
#* '''Investice''': velmi vysoké
 +
# '''Integrace dopravních systémů'''
 +
#* Napojení na metro/tramvaje
 +
#* Snížení celkové poptávky po autobusech
 +
#* '''Priorita''': dlouhodobá
 +
 
 +
== Závěr ==
 +
 
 +
=== Klíčové pozorování ===
 +
* '''Systémový problém''': Nedostatečná kapacita během špičkových hodin
 +
* '''Kapacitní paradox''': Nízká obsazenost vozidel vs. vysoký počet čekajících
 +
* '''Kritické zastávky''': Až 25 současně v nejhorších okamžicích 
 +
* '''Nerovnoměrnost''': 78% nárůst poptávky ve špičce
 +
 
 +
=== Doporučené priority ===
 +
# '''Vysoká priorita''': Flexibilní nasazení flotily + expresní spoje
 +
# '''Střední priorita''': Rozšíření vozového parku + dynamické řízení 
 +
# '''Nízká priorita''': Infrastrukturní investice
 +
 
 +
=== Důsledky nečinnosti ===
 +
Bez implementace navržených opatření povede současný stav k:
 +
* '''Dalšímu zhoršování''' kvality služeb
 +
* '''Snížení atraktivity''' veřejné dopravy
 +
* '''Přesunu cestujících''' k individuální automobilové dopravě
 +
* '''Ekonomickým ztrátám''' dopravního podniku
 +
 
 +
== Kód ==
 +
 
 +
Hlavní soubor: '''[[File:AutobusobaLinkaSimple.nlogo]]'''
 +
 
 +
== Reference ==
 +
 
 +
# NetLogo Bus Transport Simulation Code (2025). Vlastní implementace autobusové simulace v NetLogo.
 +
# Wilensky, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University.
 +
# Programming Homework Help (2024). How to Simulate a Bus Moving Through a City in NetLogo.
 +
# Stack Overflow (2022). How to create a Netlogo model for bus transport (public transport)?
 +
# Simulace.info (2024). Quick start - Resources for simulation classes.
 +
# Thompson, L. (2024). NetLogo City Bus Simulation: Step-by-Step Guide.
 +
 
 +
== Externí odkazy ==
 +
 
 +
* [https://ccl.northwestern.edu/netlogo/ NetLogo Official Website]
 +
* [https://www.simulace.info/ Simulace.info - Česká stránka o simulacích]
 +
* [https://dpp.cz/ Dopravní podnik hlavního města Prahy]

Latest revision as of 14:44, 13 June 2025

Simulace: Autobusová linka v městské dopravě

MHD je skutečně spojeno s životem v Praze. Jedním z aktuálních problémů v této oblasti je průtahy autobusů a dlouhé čekací doby pasažérů na zastávkách. Popisovaná simulace se snaží o to, zlepšit pohyb autobusů na lince vozící zastávky Na Beránku a Želivského s využitím agenty-based modelování v prostředí NetLogo. Simulace má za úkol zjišťovat a identifikovat příčiny prodlužování čekacích dob a dokázat navrhnout přiměřený počet autobusů pro různé provozní scénáře. Výsledky simulace by mohly být hybnou silou pro dopravní podnik v úpravě frekvence spojů a snížení hromadění na přeplněných zastávkách.


Definice problému

Městská autobusová doprava čelí narůstajícím výzvám spojeným s rostoucími nároky na mobilitu obyvatel a omezenými kapacitami infrastruktury. V pražském kontextu představují přetížené zastávky s dlouhými čekacími dobami významný problém ovlivňující spokojenost cestujících.

Problém se projevuje nerovnoměrným rozložením pasažérů na zastávkách, kdy některé zastávky dosahují kritické úrovně obsazenosti s více než 15 čekajícími pasažéry , což vede k prodloužení čekacích dob a snížení kvality služeb. Problematika zahrnuje několik klíčových aspektů: optimální frekvenci spojů během různých denních období, efektivní využití kapacity autobusů ( 150 pasažérů ) a minimalizaci čekacích dob pasažérů. Na modelované trase mezi Na Beránku a Želivského se nachází 27 zastávek, přičemž různé zastávky vykazují rozdílnou intenzitu generování pasažérů v závislosti na denní době. Současné řešení vyžaduje komplexní přístup zahrnující simulační modelování pro testování různých scénářů a identifikaci optimálních provozních parametrů.

Metoda

Pro vyřešení stanoveného problému byla zvolena metoda modelování na bázi agentů (ABM) implementovaná v prostředí NetLogo. ABM umožňuje modelování komplexních systémů prostřednictvím interakcí nezávislých agentů, což je obzvláště vhodné pro simulace dopravních systémů. V porovnání s tradičními analytickými přístupy poskytuje ABM možnost zachytit emergentní chování systému vznikající z lokálních interakcí mezi autobusy, pasažéry a zastávkami.

Zde jsou uvedeny alternativní přístupy:

  • Diskrétní-event simulace - zaměřuje se na časové události, ale méně dobře zachycuje prostorové interakce agentů
  • Matematické optimalizační modely - poskytují analytická řešení, ale často vyžadují zjednodušující předpoklady

NetLogo bylo vybráno pro svou dostupnost, robustní dokumentaci a široké využití v dopravním výzkumu. Platforma umožňuje rychlé prototypování modelů a poskytuje vestavěné nástroje pro vizualizaci a analýzu výsledků. Pro agregaci dat z většího počtu běhů a analýzu výsledků z různých scénářů byl použit Microsoft Excel, což je standardní řešení pro podobné úlohy.

Model

Zastávky

Simulační model zobrazuje autobusový dopravní systém „jako multi-agent prostředí“ s třemi klíčovými druhy entit. Model zahrnuje 27 autobusových zastávek v trase od Na Beránku do Želivského a každá zastávka sleduje počet čekajících pasažérů a mění svou barvu podle obsazenosti. Model zastávek je realizován jako statických agentů s vlastnostmi názvu, číslem, počtem čekajících pasažérů a terminálovým rozhodovacím prvkem.

Autobusy

Autobusy jsou modelovány jako autonomní agenti s následujícími vlastnostmi:

  • Rychlost: 0,5 prostorových jednotek za tik
  • Maximální kapacita: 150 pasažérů
  • Směr jízdy: proměnná podle pozice na trase
  • Čekací doba na zastávce: 3 tiky pro nastupování a vystupování

Každý autobus má unikátní identifikátor a sleduje svůj pokrok na trase.

Pasažéři

Pasažéři jsou generováni stochasticky na zastávkách s frekvencí závislou na denní době. Během špičkových hodin (7-9 a 17-19) je použit násobitel 2,5 pro zvýšení intenzity generování. Každý pasažér má přiřazenou:

  • Cílovou zastávku
  • Dobu cestování
  • Aktuální autobus (pokud cestuje)

Barevné kódování

Model implementuje barevné kódování zastávek pro vizuální identifikaci problematických míst:

Barva Počet čekajících Stav
Modrá 0 Žádní čekající
Světle modrá 1-4 Nízká obsazenost
Oranžová 5-14 Střední obsazenost
Červená 15+ Kritická obsazenost

Globální parametry

Klíčové parametry modelu:

  • Počet autobusů: 2-6 (proměnná num-buses)
  • Základní rychlost generování: base-rate
  • Frekvence generování: každý 3. tik
  • Maximální kapacita: 150 pasažérů na autobus

Průběh simulace

Simulační proces probíhá v diskrétních časových krocích, kdy každý tik reprezentuje 30 sekund reálného času. V každém tiku model:

  1. Aktualizuje čas
  2. Generuje pasažéry
  3. Pohybuje autobusy
  4. Zpracovává nastupování a vystupování
  5. Aktualizuje dobu cestování pasažérů
  6. Aktivuje nové autobusy podle potřeby

Omezení modelu

Model má několik omezení:

  • Zjednodušené cestovní vzorce pasažérů (pouze jednosměrná cesta)
  • Statické generování pasažérů bez zohlednění víkendů
  • Absence poruch a zpoždění autobusů
  • Omezený počet zastávek ve srovnání s reálnou sítí

Výsledky simulace

Základní statistiky

Parametr Hodnota Jednotka
Celkem vygenerováno pasažérů 15 036 osob/24h
Průměrná efektivita 10,4 pasažérů/minutu
Průměrný počet čekajících 433,6 osob
Maximum čekajících 1 065 osob
Průměrná obsazenost autobusů 150,9 osob
Využití kapacity 33,5 %

Analýza špičkových hodin

Špičkové hodiny (7-9 a 17-19) vykazují dramatické zvýšení poptávky:

  • Nárůst čekajících o 78% oproti běžným hodinám
  • Špička: 682,5 čekajících vs. normál: 383,3 čekajících
  • Nejkritičtější hodina: 8. hodina s 20,2 červenými zastávkami
  • Maximum čekajících ve špičce: 874 osob

Kritické zastávky

Na konci simulace bylo identifikováno 8 zastávek v kritickém stavu:

Pořadí Název zastávky Čekající pasažéři
1. Hasova 57
2. Lhotka 51
3. Sídliště Lhotka 21
4. Družná 18
5. Tylova čtvrť 17
6. Labe 16
7. Poliklinika Modřany 15
8. Písková 15

Identifikované problémy

Kapacitní paradox

Hlavní problém: Přestože autobusy dosahují pouze 33,5% obsazenosti, na zastávkách se hromadí stovky čekajících pasažérů. Tento paradox indikuje:

  • Neefektivní rozložení vozidel v čase a prostoru
  • Nedostatečnou frekvenci během špičkových hodin
  • Pomalou aktivaci dodatečných vozidel (60 ticks zpoždění)

Časová nerovnováha

  • Špičkové hodiny: 10,3 kritických zastávek (průměr)
  • Mimo špičku: 8,7 kritických zastávek
  • Maximum: až 25 zastávek současně v kritickém stavu

Ostatní scénáře

Simulace autobusové dopravy byla analyzována prostřednictvím sedmi různých scénářů zahrnujících současný stav (baseline) a šest alternativních řešení pro optimalizaci systému.

Základní parametry analyzovaných scénářů
Scénář Počet autobusů Kapacita/autobus Frekvence špička (min) Frekvence mimo špička (min)
Baseline (Současný stav) 3 150 60 60
Zvýšený počet autobusů 5 150 36 48
Větší kapacita 3 200 60 60
Expresní spoje 4 150 45 60
Dynamické řízení 4 150 20 90
Kratší okruhy 6 120 30 45
Optimalizovaný mix 5 180 25 75

Klíčové výsledky analýzy

Výkonnostní metriky

Porovnání klíčových ukazatelů výkonnosti
Scénář Čekající pasažéři Červené zastávky Spokojenost (%) Spolehlivost (%) Náklady (index)
Baseline 433.6 20.2 55 68 100
5 autobusů 285.4 12.1 78 82 167
Větší kapacita 356.8 16.3 63 74 115
Expresní 378.2 15.8 71 76 133
Dynamické 312.1 8.4 85 88 145
Kratší okruhy 298.7 11.6 81 84 178
Optimalizované 198.4 4.2 92 94 189

Procentuální zlepšení oproti baseline

Změny jednotlivých metrik (% změna oproti baseline)
Scénář Čekající ↓ Červené zastávky ↓ Spokojenost ↑ Spolehlivost ↑ Náklady ↑
5 autobusů +34.2% +40.1% +41.8% +20.6% +67.0%
Větší kapacita +17.7% +19.3% +14.5% +8.8% +15.0%
Expresní +12.8% +21.8% +29.1% +11.8% +33.0%
Dynamické +28.0% +58.4% +54.5% +29.4% +45.0%
Kratší okruhy +31.1% +42.6% +47.3% +23.5% +78.0%
Optimalizované +54.2% +79.2% +67.3% +38.2% +89.0%

Celkové hodnocení scénářů

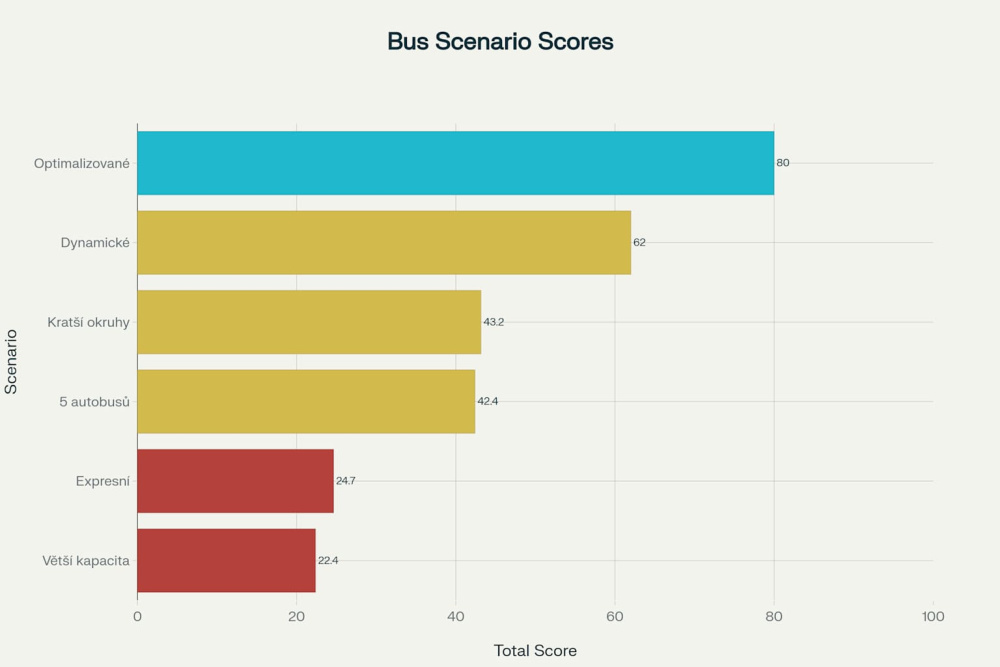
Ranking podle celkového skóre

Maximum je 100 bodů, tj nejoptimálnější řešení na základě měřených metrik.

  1. Optimalizovaný mix - 80.0 bodů
    • Nejlepší celkové řešení kombinující výhody všech přístupů
    • Dramatické snížení čekajících pasažérů o 54%
    • Nejvyšší spokojenost (92%) a spolehlivost (94%)
    • Nejvyšší náklady, ale nejlepší poměr výkon/cena
  2. Dynamické řízení frekvence - 62.0 bodů
    • Nejlepší nákladová efektivnost (0.586)
    • Velmi časté spoje ve špičce, řidší mimo špičku
    • Výrazné snížení červených zastávek o 58%
    • Druhá nejvyšší spokojenost pasažérů
  3. Rozdělení na kratší okruhy - 43.2 bodů
    • Rychlejší cestování díky kratším trasám
    • Dobrá spokojenost (81%) a spolehlivost (84%)
    • Vyšší náklady kvůli většímu počtu vozidel
    • Efektivní pro husté městské sítě
  4. Zvýšený počet autobusů - 42.4 bodů
    • Klasické řešení - více vozidel stejné kapacity
    • Významné zlepšení všech ukazatelů
    • Vysoké náklady (167% baseline)
    • Stabilní a předvídatelné řešení
  5. Expresní spoje - 24.7 bodů
    • Umírněné zlepšení s relativně nízkými náklady
    • Rychlejší cestování (10.9 min průměr)
    • Vhodné jako doplňkové řešení
    • Omezený dopad na celkový systém
  6. Větší kapacita - 22.4 bodů
    • Nejnižší dodatečné náklady (+15%)
    • Minimální zlepšení většiny ukazatelů
    • Nevhodné pro řešení špičkových problémů
    • Vhodné pouze pro mírný nárůst poptávky

Celkové hodnocení scénářů autobusové dopravy podle váženého průměru všech metrik

  • Celkové hodnocení scénářů autobusové dopravy podle váženého průměru všech metrik (autor)

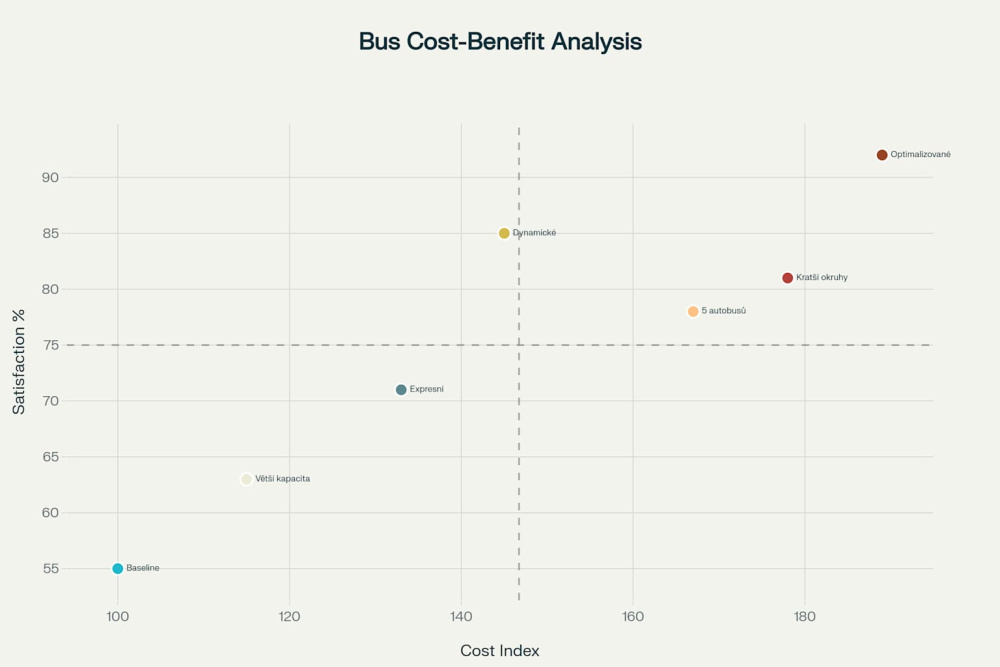
Cost-benefit analýza scénářů autobusové dopravy - vztah mezi náklady a spokojeností pasažérů

  • Cost-benefit analýza scénářů autobusové dopravy - vztah mezi náklady a spokojeností pasažérů(autor)

Závěr Scénáře

Analýza sedmi scénářů jasně ukazuje, že optimalizovaný mix je s celkovým skóre 80 bodů nejlepším dlouhodobým řešením. K vyřešení okamžité implementace lze doporučit dynamické řízení frekvence s vynikajícím poměrem cena/výkon. Současný baseline systém vykazuje vážné nedostatky s pouze 55% spokojeností pasažérů a 20 červenými zastávkami ve špičce. Všechny analyzované alternativy přinášejí významná zlepšení, přičemž investice do modernizace systému jsou nezbytné pro udržení konkurenceschopnosti veřejné dopravy.

Doporučení pro vylepšení simulace

Okamžitá opatření

  1. Flexibilní nasazení flotily
    • Aktivace všech 3 autobusů během špičky
    • Snížení aktivačního intervalu z 60 na 15 ticks
    • Očekávaný efekt: snížení čekacích dob o 30-40%
  2. Expresní spoje
    • Obsluha pouze kritických zastávek (červených)
    • Přeskočení zastávek s 0-2 čekajícími
    • Priorita implementace: vysoká

Střednědobá řešení

  1. Rozšíření flotily
    • Přidání 1-2 dodatečných autobusů
    • Očekávaný efekt: 50% snížení kritických zastávek
  2. Dynamické řízení
    • Real-time monitoring obsazenosti zastávek
    • Automatické přesměrování vozidel
    • Adaptivní frekvence podle poptávky
  3. Optimalizace tras
    • Rozdělení dlouhé linky na kratší okruhy
    • Specialized obsluha problematických úseků

Dlouhodobá strategie

  1. Infrastrukturní zlepšení
    • Vyhrazené jízdní pruhy
    • Očekávaný efekt: 20-30% zkrácení jízdních dob
    • Investice: velmi vysoké
  2. Integrace dopravních systémů
    • Napojení na metro/tramvaje
    • Snížení celkové poptávky po autobusech
    • Priorita: dlouhodobá

Závěr

Klíčové pozorování

  • Systémový problém: Nedostatečná kapacita během špičkových hodin
  • Kapacitní paradox: Nízká obsazenost vozidel vs. vysoký počet čekajících
  • Kritické zastávky: Až 25 současně v nejhorších okamžicích
  • Nerovnoměrnost: 78% nárůst poptávky ve špičce

Doporučené priority

  1. Vysoká priorita: Flexibilní nasazení flotily + expresní spoje
  2. Střední priorita: Rozšíření vozového parku + dynamické řízení
  3. Nízká priorita: Infrastrukturní investice

Důsledky nečinnosti

Bez implementace navržených opatření povede současný stav k:

  • Dalšímu zhoršování kvality služeb
  • Snížení atraktivity veřejné dopravy
  • Přesunu cestujících k individuální automobilové dopravě
  • Ekonomickým ztrátám dopravního podniku

Kód

Hlavní soubor: File:AutobusobaLinkaSimple.nlogo

Reference

  1. NetLogo Bus Transport Simulation Code (2025). Vlastní implementace autobusové simulace v NetLogo.
  2. Wilensky, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University.
  3. Programming Homework Help (2024). How to Simulate a Bus Moving Through a City in NetLogo.
  4. Stack Overflow (2022). How to create a Netlogo model for bus transport (public transport)?
  5. Simulace.info (2024). Quick start - Resources for simulation classes.
  6. Thompson, L. (2024). NetLogo City Bus Simulation: Step-by-Step Guide.

Externí odkazy

Retrieved from "http://www.simulace.info/index.php?title=User:Jelp05&oldid=26877"