Difference between revisions of "Monte Carlo method application in simulations/cs"
(→Simulaci Monte Carlo lze rozdělit do několika kroků:) |
(→Simulaci Monte Carlo lze rozdělit do několika kroků:) |
||
| Line 41: | Line 41: | ||
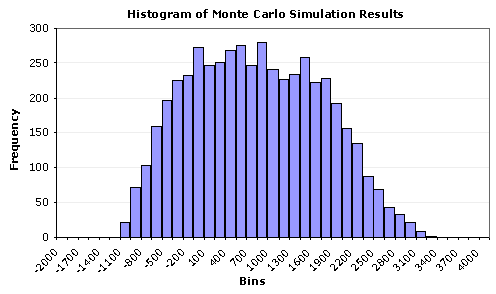
Dalším důležitým krokem je stanovení rizikových faktorů, tedy těch veličin, které budou významně ovlivňovat nejistotu výstupů simulace. Mezi těmito faktory jistě budou takové, na jejichž změny jsou výstupy simulace značně citlivé.[[File:Histogram.JPG|thumb|500px|right|Obrázek 2: Výstup simulace Monte Carlo, zdroj:]] | Dalším důležitým krokem je stanovení rizikových faktorů, tedy těch veličin, které budou významně ovlivňovat nejistotu výstupů simulace. Mezi těmito faktory jistě budou takové, na jejichž změny jsou výstupy simulace značně citlivé.[[File:Histogram.JPG|thumb|500px|right|Obrázek 2: Výstup simulace Monte Carlo, zdroj:]] | ||
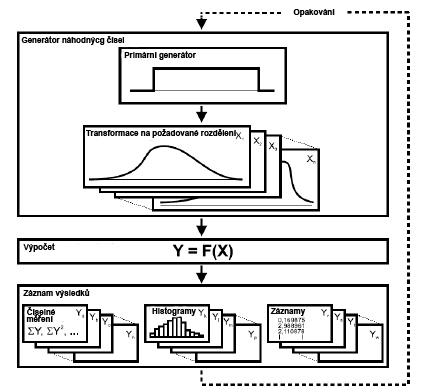
| − | '''5. Stanovení rozdělení pravděpodobnosti klíčových rizikových faktorů''' | + | [[File:MetodaMonteCarlo_postup.JPG|thumb|500px|Obrázek 3: Schéma postupu [[Monte_Carlo_method/cs|metody Monte Carlo]], zdroj:]]'''5. Stanovení rozdělení pravděpodobnosti klíčových rizikových faktorů''' |
K zajištění úspěšného použití [[Monte_Carlo_method/cs|metody Monte Carlo]] je nezbytné správně určit rozdělení pravděpodobností rizikových faktorů. V předchozím kroku jsme identifikovali klíčové rizikové faktory a nyní pro ně musíme stanovit rozdělení pravděpodobnosti. U diskrétních faktorů rizika (faktory s několika málo hodnotami) má rozdělení pravděpodobnosti tabulkový tvar a u spojitých rizikových faktorů se běžně volí určitý typ rozdělení a zadávají se jeho parametry. V případě, že máme k dispozici historická data určitého faktoru, můžeme využít ke stanovení jeho rozdělení aproximace nějakým teoretickým rozdělením. Pokud historická data k dispozici nemáme, je nutné vycházet ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů. | K zajištění úspěšného použití [[Monte_Carlo_method/cs|metody Monte Carlo]] je nezbytné správně určit rozdělení pravděpodobností rizikových faktorů. V předchozím kroku jsme identifikovali klíčové rizikové faktory a nyní pro ně musíme stanovit rozdělení pravděpodobnosti. U diskrétních faktorů rizika (faktory s několika málo hodnotami) má rozdělení pravděpodobnosti tabulkový tvar a u spojitých rizikových faktorů se běžně volí určitý typ rozdělení a zadávají se jeho parametry. V případě, že máme k dispozici historická data určitého faktoru, můžeme využít ke stanovení jeho rozdělení aproximace nějakým teoretickým rozdělením. Pokud historická data k dispozici nemáme, je nutné vycházet ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů. | ||
Revision as of 21:14, 18 June 2015
Contents
Úvod
| Budoucnost nelze plánovat pouze na základě historických údajů, jelikož vždy se mohou objevit nějaké náhodné jevy, které ji mohou jak pozitivně tak i negativně ovlivnit. Lepší pohled na budoucnost než vycházení z historických čísel nám poskytuje právě metoda Monte Carlo. |
Metodu Monte Carlo lze uplatnit v řadě simulací různého typu ať z oblasti hazardních her, projektového managementu, financí, pojišťovnictví, techniky či například i matematiky. Některé oblasti použití jsou blíže vysvětleny níže v tomto textu. Tuto metodu lze využít především v simulacích, ve kterých je řešení problému jistým způsobem závislé na pravděpodobnostech. Podstatou této metody je generování velkého počtu scénářů pomocí pseudonáhodných čísel. Tato pseudonáhodná čísla jsou generována na základě pravděpodobnostního rozdělení, které vychází z historických údajů nebo ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů. Metoda Monte Carlo tedy vnáší do modelu náhodou veličinu, která vyjadřuje to, že budoucnost se může od minulosti nějakým způsobem vychýlit.
Metodu Monte Carlo vyžaduje po zainteresovaných stranách, aby hlouběji přemýšleli nad jednotlivými rizikovými faktory. Velmi důležitým krokem je také stanovení rozdělení pravděpodobnosti daných rizikových faktorů, které není vždy snadným úkolem. Toto rozdělení bývá většinou stanoveno na obecných vlastnostech či expertních analýzách.
Postup při simulaci Monte Carlo
Než začneme provádět simulaci, je důležité si ujasnit otázku, na niž pomocí simulačního modelu budeme hledat odpověď. Dalším důležitým krokem je určení základních částí modelu a zajištění, aby těmto částem rozuměly všechny zainteresované strany. V případě, že by došlo k nepochopení, mohl by nastat problém v pozdějším zamítnutí čí požadavku na přepracování, čemuž je samozřejmě nejlepší předcházet. K lepšímu pochopení nám může pomoci tzv. influenční diagram viz. obrázek 1, který umožňuje jasně a přehledně zachytit základní prvky simulačního modelu a jejich vzájemné vazby.
Pro snazší orientaci a pochopení je dobré rozlišovat mezi hlavními prvky influenčního diagramu. Je důležité rozeznávat:
- proměnné, jejichž hodnotu můžeme (do určité míry) ovlivnit,
- rizikové faktory, které nemůžeme přímo ovlivnit,
- kriteriální proměnnou, tedy proměnnou, kterou chceme pomocí modelu analyzovat.
Vzájemné vazby mezi prvky modelu značíme šipkami. Lze také modelovat více úrovní diagramu například náklady můžeme rozdělit na fixní a variabilní, marketingové výdaje na online a offline atd.
Pokud všechny zainteresované strany rozumí základním prvkům modelu, vazbám mezi nimi a cíli modelu, lze začít sestavovat model například v nástroji MS Excel, který se následně rozšíří o simulace Monte Carlo.
Simulaci Monte Carlo lze rozdělit do několika kroků:
1. Stanovení cíle
Nejdříve je důležité jasně definovat, čeho má být dosaženo a pomocí jakých veličin (například zisk, marže atd.).
2. Tvorba deterministického matematického modelu
V dalším kroku sestavíme deterministický matematický model, který by měl popisovat určitou reálnou situaci, měl by ji skutečně vyjadřovat, ale zároveň by neměl být příliš složitý. Tento model se vyznačuje tím, že v něm nalezneme pouze nenáhodná čísla. Při tvorbě modelu je nutné dbát na rozdělení vstupních a výstupních veličin.
3. Tvorba stochastického modelu
V tomto kroku vytvoříme stochastický model, který se bude od deterministického lišit v tom, že některé parametry uvažujeme jako náhodné veličiny. Tento model se přibližuje reálným dějům, ve kterých je náhodná veličina také obvykle přítomná. Nelze říci, že stochastický model odpovídá reálné situaci zcela přesně, ale s určitou pravděpodobností. Výstupem modelu je funkce náhodných veličin a konstant.
4. Určení klíčových rizikových faktorů
Dalším důležitým krokem je stanovení rizikových faktorů, tedy těch veličin, které budou významně ovlivňovat nejistotu výstupů simulace. Mezi těmito faktory jistě budou takové, na jejichž změny jsou výstupy simulace značně citlivé.
5. Stanovení rozdělení pravděpodobnosti klíčových rizikových faktorů
K zajištění úspěšného použití metody Monte Carlo je nezbytné správně určit rozdělení pravděpodobností rizikových faktorů. V předchozím kroku jsme identifikovali klíčové rizikové faktory a nyní pro ně musíme stanovit rozdělení pravděpodobnosti. U diskrétních faktorů rizika (faktory s několika málo hodnotami) má rozdělení pravděpodobnosti tabulkový tvar a u spojitých rizikových faktorů se běžně volí určitý typ rozdělení a zadávají se jeho parametry. V případě, že máme k dispozici historická data určitého faktoru, můžeme využít ke stanovení jeho rozdělení aproximace nějakým teoretickým rozdělením. Pokud historická data k dispozici nemáme, je nutné vycházet ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů.
6. Stanovení statistické závislosti rizikových faktorů
Nesmíme opomenout, že některé rizikové faktory mohou být závislé na některých jiných faktorech. V případě, že nějakou závislost zjistíme, je důležité ji při simulaci respektovat, jinak by výsledky simulace byly zkreslené. Příkladem statistické závislosti je například poptávka po určitém zboží, která může být závislá na prodejní ceně tohoto zboží, pokud cena stoupá, poptávka po tomto zboží klesá a naopak.
7. Provedení simulace pomocí počítačového programu
Počítačový program (například MS Excel, Crystal Ball, Matlab, ModelRisk atd.) provádí velký počet scénářů, které se opakují až do konce simulace. Konec simulace nastává provedením posledního scénáře ze stanoveného počtu. V každém simulačním kroku jsou programem vygenerovány možné hodnoty rizikových faktorů z jejich rozdělení pravděpodobnosti a je propočteno výstupní kritérium. Každý tento simulační krok neboli scénář odpovídá jednomu možnému vývoji reálné situace. Po proběhnutí dostatečného počtu simulačních kroků dostaneme výsledky, které mohou být interpretovány jak graficky tak i číselně. Graficky mohou být výstup interpretovány například pomocí histogramu, funkce hustoty či pomocí číselných charakteristik, kterými jsou průměr, medián, horní, dolní kvartil atd.

Druhy simulací
Hazardní hry
Hru lze považovat za posloupnost tahů (konečnou) prováděných v určitém pořadí a popisující každý tah. Tahy můžeme rozdělit na osobní tahy, které závisí na vůli hráče, náhodné tahy, které na hráči vůbec nezávisí a smíšené tahy, kdy je výsledek tahu kombinací záměru hráče a náhody. Monte Carlo je ukázkou procesů, kdy systém osobních tahů bude simulovat systém náhodných tahů. Hry založené na náhodě jsou nazývány jako hazardní hry. Mezi nejznámější a nejstarší hazardní hry patří hrací kostky, náhodný tah kuliček z urny či ruleta. Tyto hry lze simulovat pomocí metody Monte Carlo.
Metodu Monte Carlo lze velmi dobře pochopit na příkladu házení klasickou hrací kostkou. Běžný hráč se nejspíš nezamýšlí nad pravděpodobností toho, že hodí právě šestku v součtu dvou kostek (například 4+2, 3+3, 5+1). Tím, že hod kostkou nasimulujeme a tuto simulaci provedeme tisíckrát čí i mnohem víckrát, tak získáme výsledek, který nám řekne, jak je pravděpodobné, že hozená šestka bude například kombinací 4+2. Metoda Monte Carlo nám navíc umožňuje tuto simulaci provést rychle a efektivně.
Dalším příkladem, kdy lze využít metodu Monte Carlo jsou například šachy. Na trhu je k dispozici mnoho šachových programů, jejichž cílem je hledat a nacházet nejlepší možné tahy. Tyto programy se snaží napodobovat lidský mozek a očekávat soupeřovi tahy. Program zná tahy, které je možné realizovat v jednotlivých situacích, avšak některé pozice dělají šachovým programům problémy. Tento problém lze vyřešit pomocí metody Monte Carlo, která sehraje velmi mnoho rychlých šachových partií a na konci vyhodnotí statistiku výsledků. V případě, že například v pozici s krajním pěšcem a špatným střelcem algoritmus programu vyhodnotí, že má převahu k výhře, ale pomocí metody Monte Carlo zjistíme, že tisíc z tisíce rychlých partií skončí remízou, usoudí, že je pozice opravdu remízová.
Projektový management
Může se zdát, že metoda Monte Carlo nemá v projektovém managementu příliš velké uplatnění, ale opak je pravdou. Metoda Monte Carlo může pomoci projektovým manažerům lépe a přesněji predikovat vývoj projektu. Na projekt musíme nahlížet jako na množinu úkolů, které se mohou vzájemně ovlivňovat a kde můžeme každému úkolu přiřadit pravděpodobnost, s jakou se ho podaří včas dokončit. S tímto pohledem na projekt můžeme aplikovat metodu Monte Carlo a přiřadit proměnné zasazené do systému náhodných čísel v rozptylu rovnajícímu se rozptylu odhadů k danému úkolu. Tento krok provedeme pro každý úkol projektu nebo případně alespoň pro každý souhrnný úkol projektu. Na výsledné hodnoty je aplikována deterministická analýza a tento proces se opakuje, dle námi stanoveného počtu opakování (tisíce, desetitisíce atd.). Výstupem analýzy jsou data, která mají díky velkému počtu opakování dostatečnou vypovídací schopnost. Projektový manažer, tak získá podklad, který mu může pomoci v jednání o dřívějším zahájení projektu či jeho prodloužení .
Finance
Metoda Monte Carlo má ve financích široké možnosti využití. Lze ji uplatnit pro simulace v oblasti podnikových financí, oceňování opcí, dluhových cenných papírů, řízení portfolia, vývoj měnového kurzu či například osobním finančním plánování. Velmi časté uplatnění má tato metoda také v oblasti analýzy a řízení rizika, kde jsou získané výsledky přesnější než při použití jiných metod. Metoda Monte Carlo je velmi užitečná, jelikož pokud bychom analýzy zakládali pouze na historických datech, nemusely by být tyto analýzy správné, neboť budoucnost se může značně vychýlit. Metoda Monte Carlo poskytuje širokou škálu možností a navíc je velmi flexibilní, díky možnosti měnit jednotlivé rizikové faktory a tím modelovat řadu možných výstupů. K dispozici poté máme různé budoucí výsledky, které můžeme porovnávat a vyhodnocovat. Pomocí metody Monte Carlo mohou analytici a finanční poradci převést investiční příležitosti do podoby možností.
Analýza rizik
Jednou z oblastí financí, ve které se velmi často využívá metoda Monte Carlo, je analýza rizik, která slouží k vyhodnocení možných důsledků důležitých strategických rozhodnutí či dopadů významných změn ekonomické situace, což je v dnešní době také aktuálním tématem. V podnicích ji lze využít v modelování určitých situací (optimistické, pesimistické hodnoty) při tvorbě finanční plánů. Takovéto analýzy jsou ale pouze výsledkem omezeného odhadu budoucí hodnoty. Metoda Monte Carlo poslouží v analýze rizik v situacích, kdy potřebujeme získat odpověď na otázku, jaká je pravděpodobnost, že u sledované veličiny dosáhneme určitý užší rozsah.
Ostatní
Metodu Monte Carlo lze využít i v dalších oborech činnosti jako například ve fyzice, matematice, statistice či informatice. Ve fyzice se tato metoda často používá v případech, kdy kvůli nedostatku financí není možné provést reálný experiment. Aplikuje se zejména v těchto oblastech fyziky: statistická fyzika, fyzikální chemie, kvantová fyzika, aerodynamika či předpovědi počasí. V matematice se metoda Monte Carlo využívá při výpočtu určitých jednoduchých i složitých integrálů, při řešení systému lineárních algebraických rovnic, při řešení parciálních diferenciálních rovnic nebo také při hledání kořenů rovnic. Ve statistice se nejčastěji používá k testování statistických hypotéz. V informatice se využívá zejména ve hrách, jak již bylo zmíněno výše v kapitole hazardní hry, k tomu aby počítač uměl zvolit nejlepší možný tah v dané situaci.
Výhody a nevýhody metody Monte Carlo
Simulace metodou Monte Carlo vede k hlubšímu poznání rizikových faktorů. Za nevýhodu lze považovat pracnost a obtížnost související zejména se stanovením rozdělení pravděpodobnosti faktorů rizika.