User:Jelp05

Simulace: Autobusová linka v městské dopravě

MHD je skutečně spojeno s životem v Praze. Jedním z aktuálních problémů v této oblasti je průtahy autobusů a dlouhé čekací doby pasažérů na zastávkách. Popisovaná simulace se snaží o to, zlepšit pohyb autobusů na lince vozící zastávky Na Beránku a Želivského s využitím agenty-based modelování v prostředí NetLogo. Simulace má za úkol zjišťovat a identifikovat příčiny prodlužování čekacích dob a dokázat navrhnout přiměřený počet autobusů pro různé provozní scénáře. Výsledky simulace by mohly být hybnou silou pro dopravní podnik v úpravě frekvence spojů a snížení hromadění na přeplněných zastávkách.

Definice problému

Městská autobusová doprava čelí narůstajícím výzvám spojeným s rostoucími nároky na mobilitu obyvatel a omezenými kapacitami infrastruktury. V pražském kontextu představují přetížené zastávky s dlouhými čekacími dobami významný problém ovlivňující spokojenost cestujících.

Problém se projevuje nerovnoměrným rozložením pasažérů na zastávkách, kdy některé zastávky dosahují kritické úrovně obsazenosti s více než 15 čekajícími pasažéry , což vede k prodloužení čekacích dob a snížení kvality služeb. Problematika zahrnuje několik klíčových aspektů: optimální frekvenci spojů během různých denních období, efektivní využití kapacity autobusů ( 150 pasažérů ) a minimalizaci čekacích dob pasažérů. Na modelované trase mezi Na Beránku a Želivského se nachází 27 zastávek, přičemž různé zastávky vykazují rozdílnou intenzitu generování pasažérů v závislosti na denní době. Současné řešení vyžaduje komplexní přístup zahrnující simulační modelování pro testování různých scénářů a identifikaci optimálních provozních parametrů.

Metoda

Pro vyřešení stanoveného problému byla zvolena metoda modelování na bázi agentů (ABM) implementovaná v prostředí NetLogo. ABM umožňuje modelování komplexních systémů prostřednictvím interakcí nezávislých agentů, což je obzvláště vhodné pro simulace dopravních systémů. V porovnání s tradičními analytickými přístupy poskytuje ABM možnost zachytit emergentní chování systému vznikající z lokálních interakcí mezi autobusy, pasažéry a zastávkami.

Zde jsou uvedeny alternativní přístupy:

• Diskrétní-event simulace - zaměřuje se na časové události, ale méně dobře zachycuje prostorové interakce agentů

• Matematické optimalizační modely - poskytují analytická řešení, ale často vyžadují zjednodušující předpoklady

NetLogo bylo vybráno pro svou dostupnost, robustní dokumentaci a široké využití v dopravním výzkumu. Platforma umožňuje rychlé prototypování modelů a poskytuje vestavěné nástroje pro vizualizaci a analýzu výsledků. Pro agregaci dat z většího počtu běhů a analýzu výsledků z různých scénářů byl použit Microsoft Excel, což je standardní řešení pro podobné úlohy.

Model

Zastávky

Simulační model zobrazuje autobusový dopravní systém „jako multi-agent prostředí“ s třemi klíčovými druhy entit. Model zahrnuje 27 autobusových zastávek v trase od Na Beránku do Želivského a každá zastávka sleduje počet čekajících pasažérů a mění svou barvu podle obsazenosti. Model zastávek je realizován jako statických agentů s vlastnostmi názvu, číslem, počtem čekajících pasažérů a terminálovým rozhodovacím prvkem.

Autobusy

Autobusy jsou modelovány jako autonomní agenti s následujícími vlastnostmi:

• Rychlost: 0,5 prostorových jednotek za tik
• Maximální kapacita: 150 pasažérů
• Směr jízdy: proměnná podle pozice na trase
• Čekací doba na zastávce: 3 tiky pro nastupování a vystupování

Každý autobus má unikátní identifikátor a sleduje svůj pokrok na trase.

Pasažéři

Pasažéři jsou generováni stochasticky na zastávkách s frekvencí závislou na denní době. Během špičkových hodin (7-9 a 17-19) je použit násobitel 2,5 pro zvýšení intenzity generování. Každý pasažér má přiřazenou:

• Cílovou zastávku
• Dobu cestování
• Aktuální autobus (pokud cestuje)

Barevné kódování

Model implementuje barevné kódování zastávek pro vizuální identifikaci problematických míst:

Barva	Počet čekajících	Stav
Modrá	0	Žádní čekající
Světle modrá	1-4	Nízká obsazenost
Oranžová	5-14	Střední obsazenost
Červená	15+	Kritická obsazenost

Globální parametry

Klíčové parametry modelu:

• Počet autobusů: 2-6 (proměnná num-buses)
• Základní rychlost generování: base-rate
• Frekvence generování: každý 3. tik
• Maximální kapacita: 150 pasažérů na autobus

Průběh simulace

Simulační proces probíhá v diskrétních časových krocích, kdy každý tik reprezentuje 30 sekund reálného času. V každém tiku model:

1. Aktualizuje čas
2. Generuje pasažéry
3. Pohybuje autobusy
4. Zpracovává nastupování a vystupování
5. Aktualizuje dobu cestování pasažérů
6. Aktivuje nové autobusy podle potřeby

Omezení modelu

Model má několik omezení:

• Zjednodušené cestovní vzorce pasažérů (pouze jednosměrná cesta)
• Statické generování pasažérů bez zohlednění víkendů
• Absence poruch a zpoždění autobusů
• Omezený počet zastávek ve srovnání s reálnou sítí

Výsledky simulace

Základní statistiky

Parametr	Hodnota	Jednotka
Celkem vygenerováno pasažérů	15 036	osob/24h
Průměrná efektivita	10,4	pasažérů/minutu
Průměrný počet čekajících	433,6	osob
Maximum čekajících	1 065	osob
Průměrná obsazenost autobusů	150,9	osob
Využití kapacity	33,5	%

Analýza špičkových hodin

Špičkové hodiny (7-9 a 17-19) vykazují dramatické zvýšení poptávky:

• Nárůst čekajících o 78% oproti běžným hodinám
• Špička: 682,5 čekajících vs. normál: 383,3 čekajících
• Nejkritičtější hodina: 8. hodina s 20,2 červenými zastávkami
• Maximum čekajících ve špičce: 874 osob

Kritické zastávky

Na konci simulace bylo identifikováno 8 zastávek v kritickém stavu:

Pořadí	Název zastávky	Čekající pasažéři
1.	Hasova	57
2.	Lhotka	51
3.	Sídliště Lhotka	21
4.	Družná	18
5.	Tylova čtvrť	17
6.	Labe	16
7.	Poliklinika Modřany	15
8.	Písková	15

Identifikované problémy

Kapacitní paradox

Hlavní problém: Přestože autobusy dosahují pouze 33,5% obsazenosti, na zastávkách se hromadí stovky čekajících pasažérů. Tento paradox indikuje:

• Neefektivní rozložení vozidel v čase a prostoru
• Nedostatečnou frekvenci během špičkových hodin
• Pomalou aktivaci dodatečných vozidel (60 ticks zpoždění)

Časová nerovnováha

• Špičkové hodiny: 10,3 kritických zastávek (průměr)
• Mimo špičku: 8,7 kritických zastávek
• Maximum: až 25 zastávek současně v kritickém stavu

Ostatní scénáře

Simulace autobusové dopravy byla analyzována prostřednictvím sedmi různých scénářů zahrnujících současný stav (baseline) a šest alternativních řešení pro optimalizaci systému.

Základní parametry analyzovaných scénářů

Scénář	Počet autobusů	Kapacita/autobus	Frekvence špička (min)	Frekvence mimo špička (min)
Baseline (Současný stav)	3	150	60	60
Zvýšený počet autobusů	5	150	36	48
Větší kapacita	3	200	60	60
Expresní spoje	4	150	45	60
Dynamické řízení	4	150	20	90
Kratší okruhy	6	120	30	45
Optimalizovaný mix	5	180	25	75

Klíčové výsledky analýzy

Výkonnostní metriky

Porovnání klíčových ukazatelů výkonnosti

Scénář	Čekající pasažéři	Červené zastávky	Spokojenost (%)	Spolehlivost (%)	Náklady (index)
Baseline	433.6	20.2	55	68	100
5 autobusů	285.4	12.1	78	82	167
Větší kapacita	356.8	16.3	63	74	115
Expresní	378.2	15.8	71	76	133
Dynamické	312.1	8.4	85	88	145
Kratší okruhy	298.7	11.6	81	84	178
Optimalizované	198.4	4.2	92	94	189

Procentuální zlepšení oproti baseline

Změny jednotlivých metrik (% změna oproti baseline)

Scénář	Čekající ↓	Červené zastávky ↓	Spokojenost ↑	Spolehlivost ↑	Náklady ↑
5 autobusů	+34.2%	+40.1%	+41.8%	+20.6%	+67.0%
Větší kapacita	+17.7%	+19.3%	+14.5%	+8.8%	+15.0%
Expresní	+12.8%	+21.8%	+29.1%	+11.8%	+33.0%
Dynamické	+28.0%	+58.4%	+54.5%	+29.4%	+45.0%
Kratší okruhy	+31.1%	+42.6%	+47.3%	+23.5%	+78.0%
Optimalizované	+54.2%	+79.2%	+67.3%	+38.2%	+89.0%

Celkové hodnocení scénářů

Ranking podle celkového skóre

Maximum je 100 bodů, tj nejoptimálnější řešení na základě měřených metrik.

1. Optimalizovaný mix - 80.0 bodů
   • Nejlepší celkové řešení kombinující výhody všech přístupů
   • Dramatické snížení čekajících pasažérů o 54%
   • Nejvyšší spokojenost (92%) a spolehlivost (94%)
   • Nejvyšší náklady, ale nejlepší poměr výkon/cena
2. Dynamické řízení frekvence - 62.0 bodů
   • Nejlepší nákladová efektivnost (0.586)
   • Velmi časté spoje ve špičce, řidší mimo špičku
   • Výrazné snížení červených zastávek o 58%
   • Druhá nejvyšší spokojenost pasažérů
3. Rozdělení na kratší okruhy - 43.2 bodů
   • Rychlejší cestování díky kratším trasám
   • Dobrá spokojenost (81%) a spolehlivost (84%)
   • Vyšší náklady kvůli většímu počtu vozidel
   • Efektivní pro husté městské sítě
4. Zvýšený počet autobusů - 42.4 bodů
   • Klasické řešení - více vozidel stejné kapacity
   • Významné zlepšení všech ukazatelů
   • Vysoké náklady (167% baseline)
   • Stabilní a předvídatelné řešení
5. Expresní spoje - 24.7 bodů
   • Umírněné zlepšení s relativně nízkými náklady
   • Rychlejší cestování (10.9 min průměr)
   • Vhodné jako doplňkové řešení
   • Omezený dopad na celkový systém
6. Větší kapacita - 22.4 bodů
   • Nejnižší dodatečné náklady (+15%)
   • Minimální zlepšení většiny ukazatelů
   • Nevhodné pro řešení špičkových problémů
   • Vhodné pouze pro mírný nárůst poptávky

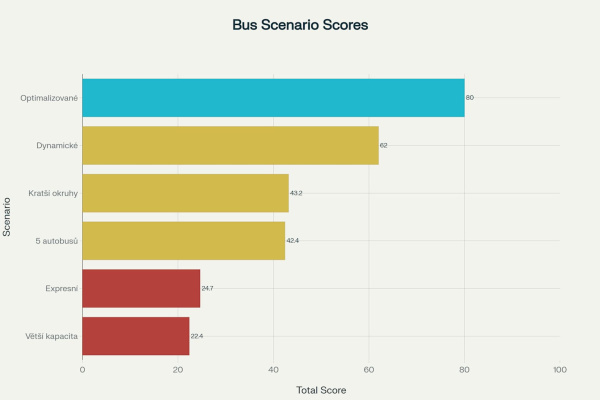Celkové hodnocení scénářů autobusové dopravy podle váženého průměru všech metrik (autor)

Závěr Scénáře

Analýza sedmi scénářů jasně ukazuje, že optimalizovaný mix představuje nejlepší dlouhodobé řešení s celkovým skóre 80 bodů. Pro okamžitou implementaci se doporučuje dynamické řízení frekvence jako nejefektivnější řešení s vynikajícím poměrem cena/výkon.

Současný baseline systém vykazuje vážné nedostatky s pouze 55% spokojeností pasažérů a 20 červenými zastávkami ve špičce. Všechny analyzované alternativy přinášejí významná zlepšení, přičemž investice do modernizace systému jsou nezbytné pro udržení konkurenceschopnosti veřejné dopravy.

Doporučení pro vylepšení simulace

Okamžitá opatření

1. Flexibilní nasazení flotily
   • Aktivace všech 3 autobusů během špičky
   • Snížení aktivačního intervalu z 60 na 15 ticks
   • Očekávaný efekt: snížení čekacích dob o 30-40%
2. Expresní spoje
   • Obsluha pouze kritických zastávek (červených)
   • Přeskočení zastávek s 0-2 čekajícími
   • Priorita implementace: vysoká

Střednědobá řešení

1. Rozšíření flotily
   • Přidání 1-2 dodatečných autobusů
   • Očekávaný efekt: 50% snížení kritických zastávek
2. Dynamické řízení
   • Real-time monitoring obsazenosti zastávek
   • Automatické přesměrování vozidel
   • Adaptivní frekvence podle poptávky
3. Optimalizace tras
   • Rozdělení dlouhé linky na kratší okruhy
   • Specialized obsluha problematických úseků

Dlouhodobá strategie

1. Infrastrukturní zlepšení
   • Vyhrazené jízdní pruhy
   • Očekávaný efekt: 20-30% zkrácení jízdních dob
   • Investice: velmi vysoké
2. Integrace dopravních systémů
   • Napojení na metro/tramvaje
   • Snížení celkové poptávky po autobusech
   • Priorita: dlouhodobá

Závěr

Klíčové pozorování

• Systémový problém: Nedostatečná kapacita během špičkových hodin
• Kapacitní paradox: Nízká obsazenost vozidel vs. vysoký počet čekajících
• Kritické zastávky: Až 25 současně v nejhorších okamžicích
• Nerovnoměrnost: 78% nárůst poptávky ve špičce

Doporučené priority

1. Vysoká priorita: Flexibilní nasazení flotily + expresní spoje
2. Střední priorita: Rozšíření vozového parku + dynamické řízení
3. Nízká priorita: Infrastrukturní investice

Důsledky nečinnosti

Bez implementace navržených opatření povede současný stav k:

• Dalšímu zhoršování kvality služeb
• Snížení atraktivity veřejné dopravy
• Přesunu cestujících k individuální automobilové dopravě
• Ekonomickým ztrátám dopravního podniku

Kód

Hlavní soubor: File:AutobusobaLinkaSimple.nlogo

Reference

1. NetLogo Bus Transport Simulation Code (2025). Vlastní implementace autobusové simulace v NetLogo.
2. Wilensky, U. (1999). NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University.
3. Programming Homework Help (2024). How to Simulate a Bus Moving Through a City in NetLogo.
4. Stack Overflow (2022). How to create a Netlogo model for bus transport (public transport)?
5. Simulace.info (2024). Quick start - Resources for simulation classes.
6. Thompson, L. (2024). NetLogo City Bus Simulation: Step-by-Step Guide.

Externí odkazy

• NetLogo Official Website
• Simulace.info - Česká stránka o simulacích
• Dopravní podnik hlavního města Prahy