Difference between revisions of "User:Kozo01"
(→Základní stavební kameny vytvořeného modelu) |
(→Základní stavební kameny vytvořeného modelu) |
||
| Line 13: | Line 13: | ||
===Základní stavební kameny vytvořeného modelu=== | ===Základní stavební kameny vytvořeného modelu=== | ||
| − | * *Poptávka na hospitalizaci* – vychází z počtu hospitalizací za rok, přepočteného na denní průměr. Abych zachytila skutečné kolísání (např. výkyvy při lokálních epidemiích, náhodné špičky), k této základní hodnotě jsem přidala gaussovský šum pomocí odpovědné funkce. | + | * * Poptávka na hospitalizaci * – vychází z počtu hospitalizací za rok, přepočteného na denní průměr. Abych zachytila skutečné kolísání (např. výkyvy při lokálních epidemiích, náhodné špičky), k této základní hodnotě jsem přidala gaussovský šum pomocí odpovědné funkce. |
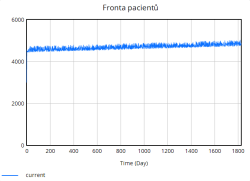
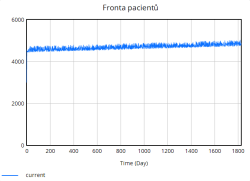
* Fronta pacientů - pokud je denní poptávka vyšší než volná kapacita lůžek, pacienti se nehospitalizují ihned, ale přecházejí do fronty. Fronta tak akumuluje neuspokojenou poptávku a uvolňuje se sem podle denních možností příjmu pacientů. Fronta představuje rozdíl mezi poptávkou a skutečným přijetím pacientů. | * Fronta pacientů - pokud je denní poptávka vyšší než volná kapacita lůžek, pacienti se nehospitalizují ihned, ale přecházejí do fronty. Fronta tak akumuluje neuspokojenou poptávku a uvolňuje se sem podle denních možností příjmu pacientů. Fronta představuje rozdíl mezi poptávkou a skutečným přijetím pacientů. | ||
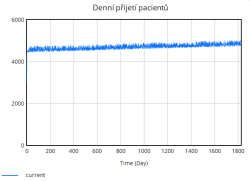
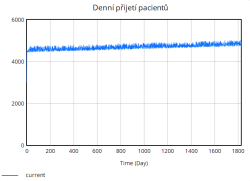
* Denní přijetí pacientů – kolik lidí skutečně se převezme na hospitalizaci, zároveň probíhá zajištění, že do péče nebude převzato víc lidí, než je dostupných lůžek. | * Denní přijetí pacientů – kolik lidí skutečně se převezme na hospitalizaci, zároveň probíhá zajištění, že do péče nebude převzato víc lidí, než je dostupných lůžek. | ||
Revision as of 23:08, 15 June 2025
Definice problému
České nemocnice disponují v průměru 4,6 akutními lůžky na 1 000 obyvatel. Při průměrné ošetřovací době, která teď činí 5,5 dne, dochází k fluktuacím mezi novými přijetími pacientů, obsazeným počtem lůžek a propouštěním pacientů. Při obsazenosti vyšší než 85 %, kvalita péče klesá, prodlužují se čekací doby a zvyšuje se riziko komplikací a nozokomiálních infekcí. Přesně toto se dělo během doby COVID-19. Simulace je vytvořena za účelem sledování vývoje obsazenosti akutních lůžek v čase a vyhodnocení dopadu různých intervencí (zkrácení průměrné ošetřovací doby, navýšení kapacity, úprava rychlosti přidávání lůžek). Výsledky simulace ukážou, která opatření nejvíce snižují riziko dlouhodobé obsazenosti nad 85 %, kdy už dochází k prodlužování čekacích dob; také případně mohou sloužit jako podpora rozhodování o investicích a rozdělení rozpočtu.
Metoda
Pro vyřešení tohoto problému byla zvolena metoda systémové dynamiky, a to konkrétně v prostředí Vensim. Tento výběr metody je odůvodněn dynamickým chováním simulovaného systému, vzájemným ovlivněním klíčových veličin jedna na druhou a také tím, že díky této metodě lze potom jednoduše ověřit jaké opatření budou schopné udržet obsazenost lůžek pod prahem bezpečného provozu.
Model
Navržený model sleduje období 5 let s časovým krokem 1 den. Je to doba, která je dost dlouhá na to, aby šlo vidět efekty od zavedení různých opatření.
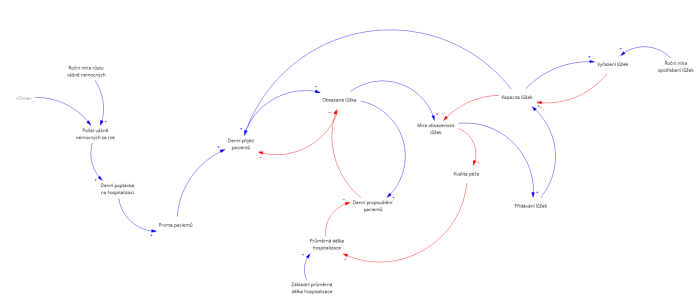
Základní stavební kameny vytvořeného modelu
- * Poptávka na hospitalizaci * – vychází z počtu hospitalizací za rok, přepočteného na denní průměr. Abych zachytila skutečné kolísání (např. výkyvy při lokálních epidemiích, náhodné špičky), k této základní hodnotě jsem přidala gaussovský šum pomocí odpovědné funkce.
- Fronta pacientů - pokud je denní poptávka vyšší než volná kapacita lůžek, pacienti se nehospitalizují ihned, ale přecházejí do fronty. Fronta tak akumuluje neuspokojenou poptávku a uvolňuje se sem podle denních možností příjmu pacientů. Fronta představuje rozdíl mezi poptávkou a skutečným přijetím pacientů.
- Denní přijetí pacientů – kolik lidí skutečně se převezme na hospitalizaci, zároveň probíhá zajištění, že do péče nebude převzato víc lidí, než je dostupných lůžek.
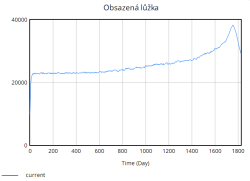
- Obsazená lůžka – tím se zachycuje aktuální počet pacientů, kteří se právě nacházejí v nemocnicích na akutních lůžkách.
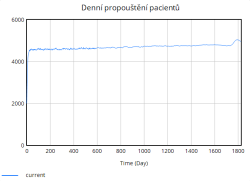
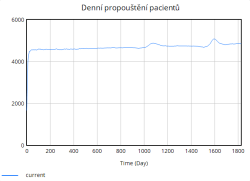
- Denní propouštění pacientů - každý den odchází z lůžek počet pacientů odpovídající průměrné délce hospitalizace– která je upravena kvalitou péče.
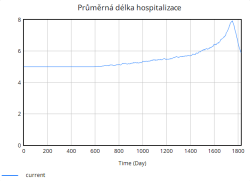
- Průměrná délka hospitalizace - tato hodnota je klíčová pro to, jak rychle se uvolňují lůžka pro nové pacienty. Čím delší pobyt, tím pomalejší obrat lůžek, a tím rychleji se nemocnice plní.
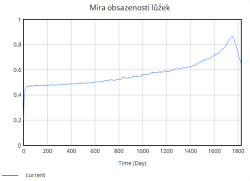
- Míra obsazenosti lůžek – důležitá proměnná pro sledování, zda nemocnice fungují v „bezpečném řežimu“; vyjadřuje, jak velký podíl z celkové lůžkové kapacity je právě obsazen. Zároveň tato proměnná je spouštěčem zásadních zpětných vazeb:
- index kvality péče klesá, když míra obsazenosti překročí prahovou hodnotu
- přidávání lůžek se aktivuje, jakmile obsazenost přesáhne nastavené hranice.
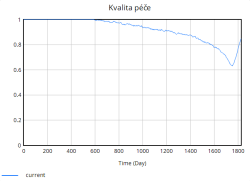
- Kvalita péče – obecně je považováno, že kvalita péče se vztahuje k rozsahu, v jakém zdravotní služby pro jednotlivce a populaci zvyšují pravděpodobnost dosažení požadovaných zdravotních výsledků, tedy přínosů pro zdraví. V případě moje simulace s rostoucí mírou obsazenosti klesá index kvality péče, což zpětně prodlužuje průměrnou délku hospitalizace.Tato vazba zároveň představuje zesilující (pozitivní) smyčku , když je vyšší zátěž, tak ta zhoršuje kvalitu, prodlužuje dobu hospitalizace, a tím dále zvyšuje obsazenost.
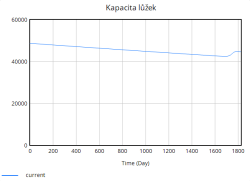
- Kapacita lůžek představuje celkový počet akutních lůžek v systému. Kapacita lůžek se mění v důsledku přidávání nových lůžek do provozu a vyřazení lůžek.
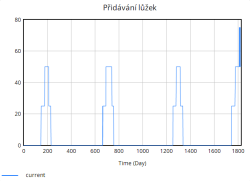
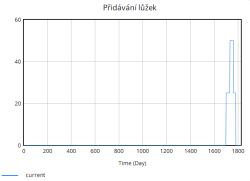
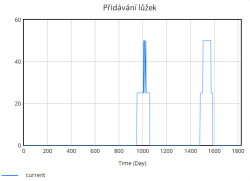
- Přidávání lůžek se zahajuje, když aktuální míra obsazenosti je vyšší než 80%, a dál čím vím roste obsazenost, tím více lůžek se aktivně přidává do provozu.
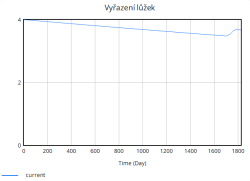
- Vyřazování lůžek: denně se vyřadí podíl z celkové kapacity stanovený roční mírou opotřebení. Děje se to především kvůli stárnutí infrastruktury.
Vstupy modelu
Model je řízen následujícími parametry, které mohou být upraveny:
- Proměnná Počet vážně nemocných za rok v modelu vyjadřuje odhad ročního počtu pacientů s těžkým průběhem onemocnění vyžadujícím hospitalizaci, který se exponenciálně navyšuje podle zadané roční míry růstu.
- Počáteční hodnota fronty pacientů = 3000
- Počáteční hodnota obsazených lůžek v ČR = 10 000
- Základní průměrná délka hospitalizace – 6 dnů
- Výchozí kapacita lůžek na celou ČR = 48698
- Prahy obsazenosti pro spouštění rozšiřování = 80–95 %.
- Roční míra opotřebení lůžek = 3%
Vstupy modelu pro vyzkoušení různých scenářů
- Snížení základní průměrné ošetřovací doby na 15% => Základní průměrná délka hospitalizace = 5
- Navýšení celkové kapacity o 10% => Kapacita lůžek = 53 568
- Navýšení počtu přidávaných lůžek o 10% při vyšší míře obsazenosti =>
- Pokud míra obsazenosti > 0.8 – přidávat 28 lůžka denně
- Pokud míra obsazenosti > 0.85 – přidávat 55 lůžka denně
- Pokud míra obsazenosti > 0.9 – přidávat 83 lůžka denně
- Pokud míra obsazenosti > 0.95 – přidávat 165 lůžka denně.
Náhodná proměnná
RANDOM NORMAL v poptávce na hospitalizaci– zachycuje nečekané výkyvy.
Proměnné modelu
- Roční míra růstu vážně nemocných = 0.013
- Počet vážně nemocných za rok = 1.91899e+06 * POWER(1 + Roční míra růstu vážně nemocných, Time/365)
- Poptávka na hospitalizaci = (Počet vážně nemocných za rok/365) + RANDOM NORMAL(1, 300, -300, 300, 1)
- Fronta pacientů = INTEG (Poptávka na hospitalizaci-Denní přijetí pacientů, Počáteční hodnota fronty)
- Denní přijetí pacientů = MIN (Fronta pacientů, Kapacita lůžek – Obsazená lůžka)
- Obsazená lůžka = INTEG (Denní přijetí pacientů-Denní propouštění pacientů, Počáteční hodnota obsazených lůžek)
- Denní propouštění pacientů = Obsazená lůžka/Průměrná délka hospitalizace
- Míra obsazeností lůžek = Obsazená lůžka/Kapacita lůžek
- Kvalita péče = IF THEN ELSE(Míra obsazeností lůžek <= 0.5,1, MAX(0,1.5 - Míra obsazeností lůžek ) )
- Základní průměrná délka hospitalizace = 6
- Průměrná délka hospitalizace = Základní průměrná délka hospitalizace/Kvalita péče
- Přidávání lůžek = IF THEN ELSE(Míra obsazeností lůžek > 0.95, 150, IF THEN ELSE(Míra obsazeností lůžek > 0.9, 75, IF THEN ELSE(Míra obsazeností lůžek > 0.85, 50, IF THEN ELSE(Míra obsazeností lůžek > 0.8, 25, 0))))
- Kapacita lůžek = INTEG (Přidávání lůžek-Vyřazení lůžek, Počáteční hodnota kapacity lůžek)
- Roční míra opotřebení = 0.03
- Vyřazení lůžek = Kapacita lůžek*Roční míra opotřebení/365
- UNITS FOR TIME = Day
- INITIAL TIME = 0
- FINAL TIME = 1825
- TIME STEP = 1
Diagram kauzálních smyček
Stock and flow diagram
Výsledky
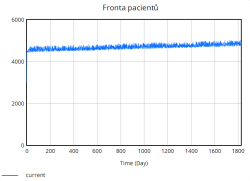
Simulace 1 - neobsahuje žádné opatření
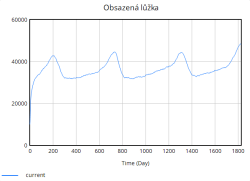
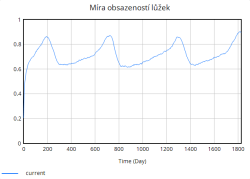
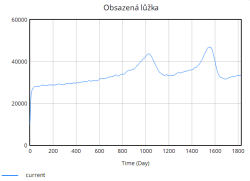
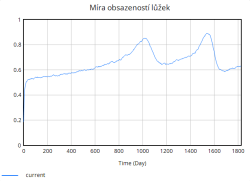
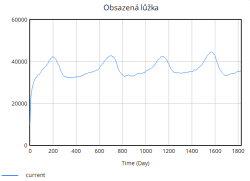
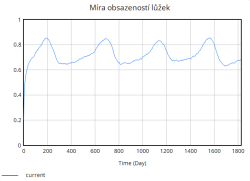
Nejdůležitější veličinou, která nás zajímá je míra obsazenosti lůžek, která jak lze vidět z grafu rychle stoupá již v úvodních dnech simulace. Zpočátku roste strmě, avšak s časem se růst zpomaluje. Důvodem tohoto zpomalení je dosažení blízkosti plné kapacity nemocnice. Jakmile se obsazenost blíží k maximální kapacitě, rychlost dalšího růstu klesá, protože nemocnice již není schopna přijímat další pacienty nad rámec své aktuální kapacity.
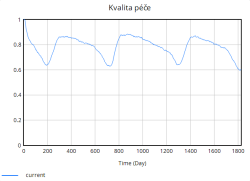
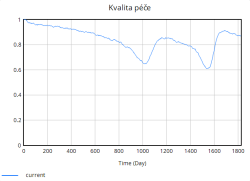
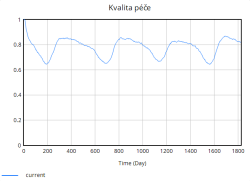
S růstem míry obsazenosti se zároveň výrazně zhoršuje kvalita péče. Graf kvality péče vykazuje periodické poklesy, které přímo souvisí s obdobím nejvyššího zatížení nemocniční kapacity. V těchto obdobích nemocnice pracuje blízko svého maxima, zdravotnický personál a vybavení jsou přetíženi, což vede k poklesu kvality poskytovaných služeb. Naopak v období nižší obsazenosti dochází k postupné regeneraci systému, díky přidávání lůžek, což se projevuje dočasným zvýšením kvality.
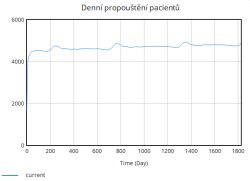
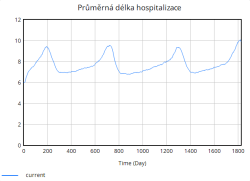
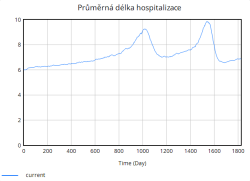
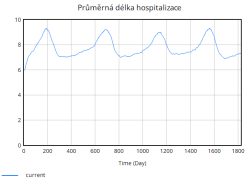
Tento cyklický průběh zatížení a uvolnění kapacity nemocnice má zásadní vliv i na průměrnou délku hospitalizace. Během období vysokého zatížení lůžkové kapacity se doba hospitalizace pacientů významně prodlužuje, jelikož se kvalita péče snižuje, personal nemůže věnovat každému pacientovi v plné míře a pacienti tak potřebují delší čas na zotavení. V období menšího zatížení je hospitalizační doba kratší a systém efektivnější.
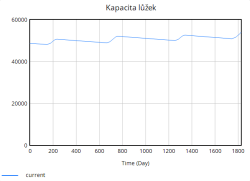
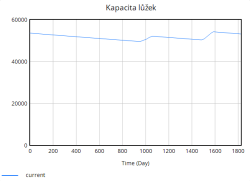
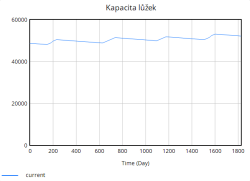
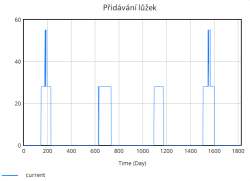
Kapacita lůžek se během simulace zvyšuje skokově díky periodickému přidávání lůžek. Tyto skokové změny odpovídají okamžikům, kdy nemocnice dosahuje kritických hodnot obsazenosti (např. 80 %, 85 %, 90 %, 95 %), a reaguje tak na zvýšený tlak na systém. Přidávání lůžek probíhá ve výrazných skocích, což je reakce na extrémní zatížení, které již nemocnice není schopna zvládnout pouze stávající kapacitou.
Na druhou stranu dochází průběžně také k vyřazování lůžek, které představuje opotřebení nebo zastarání vybavení. Tento tok je v porovnání s přidáváním relativně stabilní a pomalý, ale postupně se zvyšuje s narůstající celkovou kapacitou lůžek. Celkově simulace ukazuje, že bez vhodně zvolených opatření (např. preventivní navýšení kapacity, snížení hospitalizační doby či jiné) se systém periodicky dostává do stavů vysokého přetížení. Tyto krizové momenty se projevují poklesem kvality péče a prodlouženou hospitalizační dobou, což následně zpětně ještě více zvyšuje míru obsazenosti lůžek, a vytváří tak nežádoucí pozitivní zpětnou vazbu zhoršující situaci v nemocnici.
Simulace 2 – opatření 1- Snížení základní průměrné ošetřovací doby na 15%
Po zkracení délky hospitalizace je vidět, že to zřejmě mělo pozitivní vliv na obsazenost lůžek v nemocnicích. Po zavedení opatření se míra obsazenosti lůžek zvyšuje výrazně pomaleji, a její růst je kontrolovanější. Stabilizace nastává kolem hodnoty 0,8, což poskytuje nemocnicím určitou rezervu kapacity.
Kratší doba hospitalizace rovněž pozitivně ovlivnila kvalitu péče. Zatímco v původní simulaci bez opatření kvalita péče postupně a výrazně klesala, v této simulaci kvalita péče klesá daleko pomaleji a zůstává relativně vysoká po většinu simulace. Tento trend ukazuje, že nemocnice dokáže lépe zvládat zátěž pacientů, což je způsobeno zejména rychlejší rotací pacientů díky kratší hospitalizaci.
Kapacita lůžek se taktéž v této simulaci snižovala pomaleji než v původní variantě a na konci sledovaného období kapacita je vyšší, než kapacita na konci sledovaného období v simulaci bez zavedení opatření. Přesto se na konci sledovaného období stále projevuje pokles, který je způsoben prvním dosažením velké míry obsazenosti lůžek a taky postupným vyřazováním lůžek z důvodu opotřebení. Nicméně úplně na konci hodnota kapacity znovu roste kvůli zahájení přidávání lůžek.
Celkově, co se týče přidávání lůžek, v původní simulaci byla nutnost přidávat lůžka častější a výraznější kvůli prudkému nárůstu obsazenosti. Naopak v této simulaci se přidávání lůžek zahajuje méně často a v menším rozsahu. To potvrzuje, že opatření zkrácení průměrné délky hospitalizace pomáhá lépe řídit kapacitu a snižuje potřebu náhlého rozšiřování.
V simulaci, kde bylo zavedeno opatření 2, tak míra obsazenosti roste pomaleji než ve scénáři bez opatření, avšak dvakrát dosahuje vysokých hodnot >80%. Je to odůvodněno tím, že sice kapacita lůžek je od začátku vyšší, ale i tak po nějaké době dojde k vysoké obsazenosti, jen že se to stane po uběhnutí delší doby.
Z tohoto důvodu přiměřeně jsou ovlivněny i další ukazatele jako kvalita péče, která klesá znatelně mírněji, než v případě bez opatření, ale v polovině sledovaného období dosahuje dvakrát značného poklesu; délka hospitalizace má podobné cyklické výkyvy jako v případě bez opatření, avšak amplituda a frekvence těchto výkyvů je nižší.
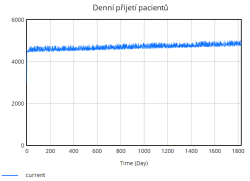
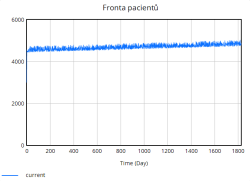
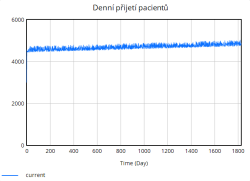
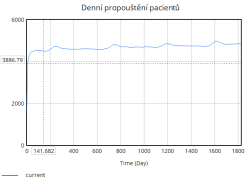
Denní příjem pacientů, fronta a propouštění pacientů vykazují podobné hodnoty jako v předchozích scénářích, avšak stabilnější prostředí způsobuje, že tyto parametry se mění rovnoměrněji bez dramatických nárůstů nebo poklesů.
Dál, díky zvýšené počáteční kapacitě potřeba přidávat nová lůžka je nižší. Vyřazení lůžek zůstává přibližně stejné, což indikuje, že udržování kapacity je jednodušší, jelikož systém se nemusí tak často dostávat na kritickou hranici.
Při aplikaci třetího opatření, kde bylo navýšení počtu přidávaných lůžek o 10% při vyšší míře obsazenosti – můžeme pozorovat podobný trend, jako v simulaci bez zavedení jakýchkoliv opatření. Navíc tady můžeme vidět, že nemocniční systém rychleji dosahuje vrcholů obsazenosti lůžek, ale taktéž rychleji se ta hodnota ponižuje kvůli tomu, že je přidáván větší počet lůžek. Počátečních kapacita lůžek se v čase roste cca o 5 % výše díky častějším dávkám přidávání lůžek.
Opatření 3 tedy zmírňuje přetížení a udržuje stabilnější provoz, ale samo o sobě nestačí k úplné eliminaci špiček – k dalšímu vylepšení by bylo vhodné zkombinovat i zkrácení ošetřovací doby nebo trvalé navýšení kapacity.
Závěr
V rámci této práce jsem vytvořila model plnění nemocniční kapacity a otestovala tři zásahy do modelu:
- Opatření 1 – zkrácení ošetřovací doby o 15 %
- Opatření 2 – navýšení základní kapacity o 10 %
- Opatření 3 – zvýšení počtu přidávaných lůžek o 10 % při vysoké obsazenosti .
Nejúčinnější se ukázalo Opatření 1, neboť zkrácení průměrné doby hospitalizace nejrychleji uvolnilo lůžka, zpomalilo růst obsazenosti a udrželo kvalitu péče větší dobu simulace nad 0,80. Díky kratším hospitalizacím se denní propouštění zvýšilo a fronta se stabilizovala kolem 4 500–4 700 pacientů.
Zavedení opatření 2 sice okamžitě zvýšilo celkovou kapacitu, avšak bez úpravy průtoku pacientů nedokázalo zabránit nárůstu obsazenosti nad 80 % v krizových špičkách. V rámci opatření 3 se přidávalo více lůžek pouze v momentu přetížení, což sice zmírnilo krátkodobé špičky, ale celkově nepřineslo tak výraznou úlevu jako zkrácení délky ošetření.
Na závěr tedy chci shrnout, že optimalizace ošetřovací doby je silnější než pouhé navyšování zdrojů. Do budoucna by model mohl být navíc rozšířen o dynamiku personálního zatížení a finanční náklady na úpravy kapacity.
Kód
File:SimulaceObsazenostiLůžek.rar