Název simulace: Vývoj sítě dobíjecích stanic v ČR

Autor: Bc. Tomáš Koťara, kott03

Typ modelu: Systémová dynamika

Modelovací nástroj: Vensim

Definice problému

V České republice roste počet elektromobilů. Ty je nutné dobíjet a i když počet dobíjecích stanice roste, díky legislativním brzdným silám, jenž způsobuje pomalé povolování staveb dobíjejích stanic, může nastat problém s nedostupností dobíjecích stanic. V souvislosti s rychlým nárůstem popularity elektromobilů se vyskytuje stále naléhavější problém efektivního a udržitelného nabíjení. Dobíjecí stanice pro elektromobily představují kritický prvek v infrastruktuře pro podporu těchto vozidel. Zatímco elektromobily jsou klíčové pro přechod k udržitelnějšímu dopravnímu systému, jejich rostoucí počet klade také nové nároky na elektrickou síť a spotřebu energie. Problém spočívá v identifikaci, jak faktory jako počet dobíjecích stanic, počet elektromobilů, rychlost nabíjení (kapacita baterií), marketingové akce a dostupnost energie (výkonu) ovlivňují spotřebu energie při nabíjení elektromobilů na veřejných dobíjecích stanicích. Tato problematika je složitá a dynamická, proto je její modelování a simulace náročná. Pomocí Vensimu lze tato problematika analyzovat a pochopit, jak jednotlivé faktory ovlivňují celkovou spotřebu energie. Simulace tak může poskytnout informace pro rozhodování o rozvoji infrastruktury pro dobíjení elektromobilů, plánování kapacity energie a strategiích pro řízení spotřeby energie.

Metoda

Cílem simulace je vytvořit zjednodušený model simulace, který bude ilustrovat poptávku a nabídku po dobíjecích stanicích v České republice. Podle nastavených parametrů lze sledovat budoucí vývoj a zjistit, kdy nastane nedostatek nabíjecích stanic. Jelikož budeme simulovat budoucí hodnotu, která je závislá na několika dalších proměnných byl pro implementaci zvolen nástroj Vensim, který je vhodný pro tento typ simulace.

Model

Model sleduje po hodinách období jednoho týdne, kdy se zpravidla uskuteční nabíjecí cyklus elektromobilu, alespoň jedenkrát.

Výchozí hodnoty o nabíjeích stanicích pochází z dat Ministerstvem průmyslu a obchodu. Data o elektromobilech pochází z portálu Čistá doprava od Centra dopravního výzkumu. Data jsou za rok 2022.

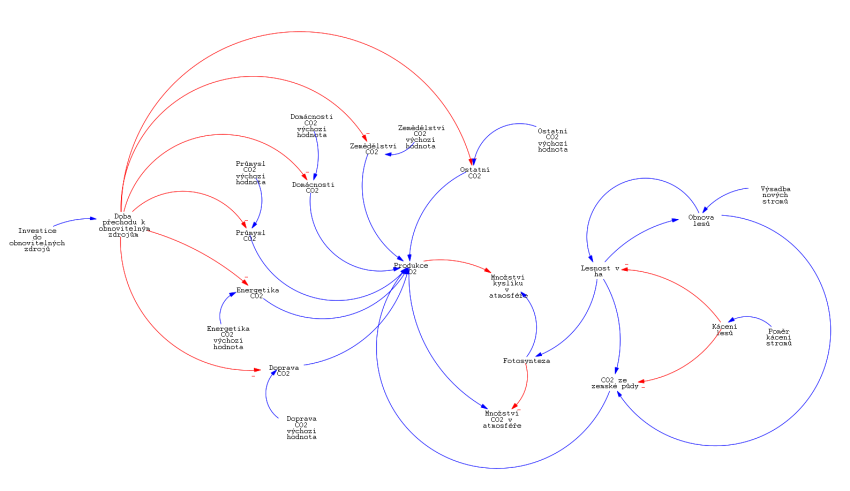
Diagram kauzálních smyček je následující.

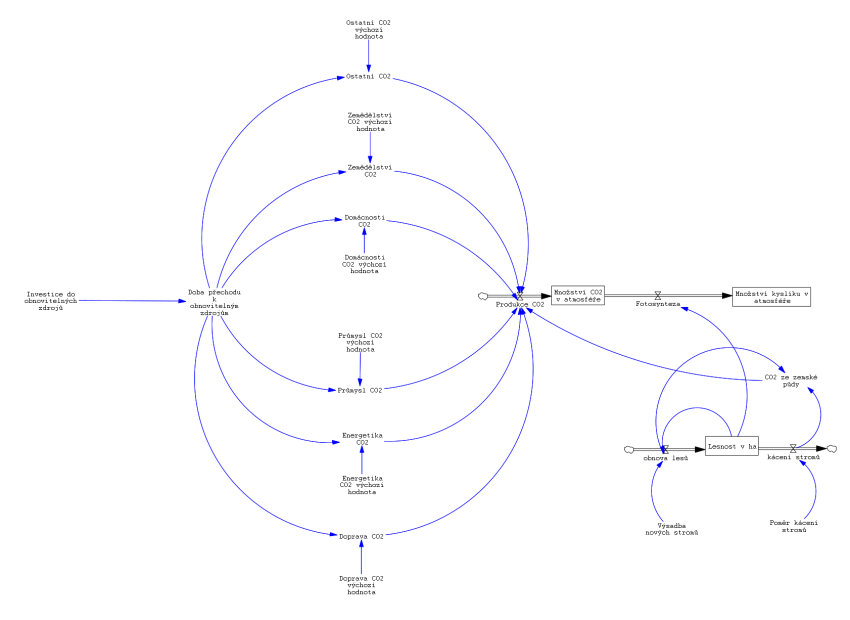
Obrázek 1: Diagram kauzálních smyček

Model kauzálních smyček byl následně přetvořen do stack and flow diagramu.

Obrázek 2: Stock and flow diagram

Proměnné modelu

Nastavení modelu je následující:

• Units for Time = Hour

• INITIAL TIME = 0

• FINAL TIME = 168

• TIME STEP = 1

Proměnné modelu jsou nastaveny následovně:

• Dobíjecí stanice ACDC = 49893 kW Zdroj

• Dobíjecí stanice DC = 9069 kW Zdroj

• Dobíjecí stanice AC = 23689 kW Zdroj

• Dostupný výkon veřejných dobíjecích stanic = (Dobíjecí stanice AC+Dobíjecí stanice ACDC+Dobíjecí stanice DC)/Marketingová akce (Dostupný výkon ze všech dobíjecích stanic ovlivněný marketingovou akcí, která dostupný výkon může snížit)

• Dostupná energie = Dostupný výkon veřejných dobíjecích stanic+IF THEN ELSE( Dobíjecí stanice>0 , Dobíjecí stanice*Přenesený výkon , 0 ) (Dostupná energie, ovlivněná přeneseným výkonem, jenž mohl nastat z minulého období, při nevyužití)

• Marketingová akce = RANDOM UNIFORM( 1 , 2 , 0.5 ) (Váha marketingové akce v intervalu od jedné do dvou)

• Účinnost dobíjecí stanice = RANDOM UNIFORM( 0.85 , 0.95 , 0.01 ) (Účinnost dobíjecí stanice, dle výrobců, se pohybuje v intervalu od 85% do 95%) Zdroj

• Kapacita baterie = RANDOM UNIFORM( 17 , 123 , 10 ) (Kapacita baterie, kdy elektromobily v současné době mají nejmenší 17 kW a největší 123 kW) Zdroj

• Nabíjení = (Kapacita baterie/Účinnost dobíjecí stanice)*Nutnost dobíjet (Kapacita baterie dělena účinností značí spotřebu energie násobenou nutností nabíjet během týdne)

• Počet elektromobilů = 14316 (Počet elektromobilů v ČR za rok 2022) Zdroj

• Denní doba = RANDOM UNIFORM( 1 , 3 , 1 ) (Náhodná hodnota simulující denní dobu a tudíž obvyklý čas nabíjení elektromobilu)

• Nutnost dobíjet = Počet elektromobilů*RANDOM UNIFORM( 0.001 , 0.003 , 0.001 )*Denní doba*Marketingová akce (Simuluje nutnost dobíjet elektromobil, dle denní doby, marketingové akce a počtu elektromobilů)

• Nabíjení = (Kapacita baterie/Účinnost dobíjecí stanice)*Nutnost dobíjet (Zobrazuje celkovou spotřebu při nabíjení v závisloti na zdrojových proměnných)

• Odchozí energie = Nabíjení+IF THEN ELSE( Dobíjecí stanice<0 , ABS( Dobíjecí stanice*Přenesený výkon ) , 0 ) (Zobrazuje celkovou odchozí energii)

• Přenesený výkon = RANDOM UNIFORM( 0.01 , 0.05 , 0.01 ) (Udává procentuální hodnotu, jenž se přenese do dalšího období)

• Dobíjecí stanice = Dostupná energie-Odchozí energie (Udává bilanci mezi dostupnou a odebíranou el. enerigií)

Výsledky

Po spuštění simulace s výchozími hodnotami model zobrazuje nutnost dobíjet v čase u elektromobilů v intervalu od 20 do 220.

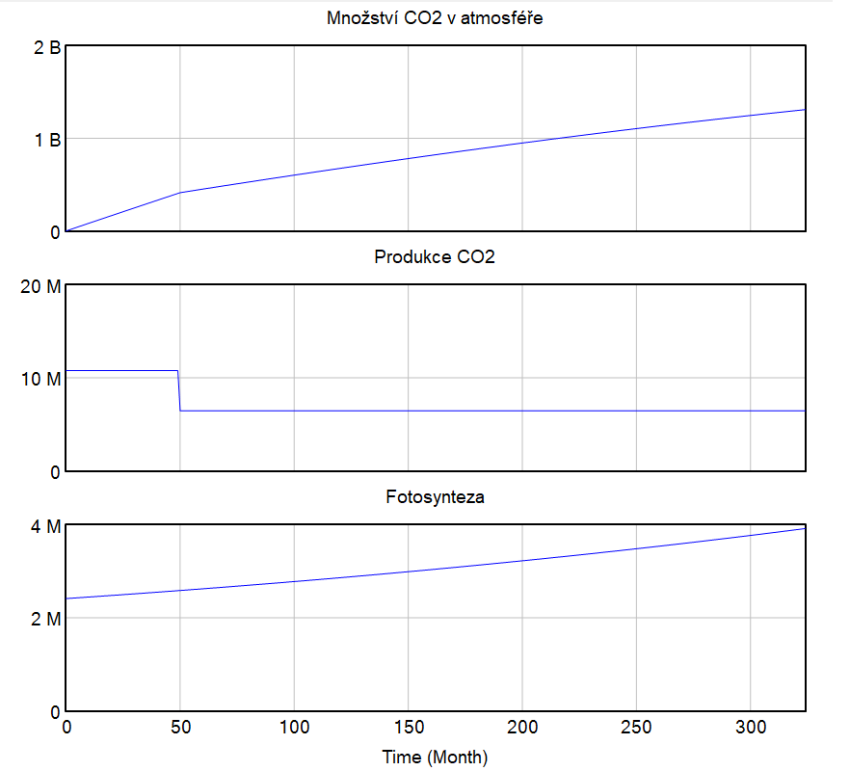
Při spuštění simulace s výchozími hodnotami vypadá model následovně. Za první měsíc Česká republika vyprodukuje celkem 10,77 mil tun CO₂. Zlomový měsíc, kdy se ČR zavázalo, že sníží svoje emise o 40 % je měsíc číslo 96 (rok 2030). Při pohledu na graf vidíme, že svůj slib ČR splnila, jelikož svoje emise v 96. měsíci snížila přibližně o 50 %.

Na grafu produkce CO₂ můžeme vidět, že s výchozím poměrem investice přijde razantní změna v produkci mezi 48-50. měsíci (za cca 4-4,2 roku)

Při pohledu na rok 2050 (324. měsíc) už tak optimistické výsledky nedostáváme, protože se produkce oxidu uhličitého nijak víc nesnížila a množství CO₂ v atmosféře se zvyšuje. Slib nulové produkce do roku 2050 tedy Česká republika nesplnila.

Obrázek 3: Výsledky první simulace s výchozími hodnotami

Pokud bychom chtěli model upravit tak, aby vyhovoval podmínkám Pařížské dohody musíme více investovat do přeměny k obnovitelným zdrojům.

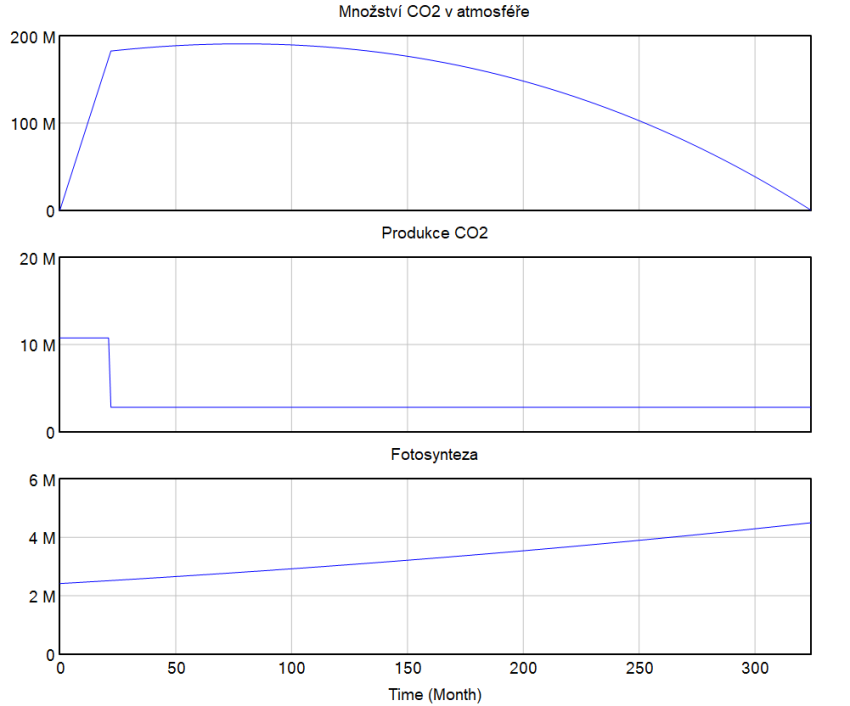
Ještě předtím ale zkusíme zvýšit výsadbu nových lesů a snížit jejich kácení. Uvědomuji si, že těžba dřeva je důležitá proto si ji snížíme z původní hodnoty na 2800 ha měsíčne. Poměr výsadby nových stromů zvýšíme na maximální hodnotu 2500 (obnova po kůrovcové kalamitě). Tím se sníží produkce CO₂ ze zemské půdy a zároveň se díky tomu zvýší podíl fotosyntézy.

Hranice splnění obou podmínek – tedy do roku 2030 snížení emisí o 40 % a do roku 2050 nulový oxid uhličitý nastává při hodnotě investic 0.74. Zvýšením investice se nám sníží i doba přechodu k obnovitelným zdrojům a tím i samotná produkce CO₂.

Obrázek 4: Výsledky simulace pro splnění podmínek Pařížské dohody

Závěr

Pokud Česká republika chce dodržet svůj závazek vůči Pařížské dohodě, musí podporovat a investovat více úsilí a financí do oblasti obnovitelných zdrojů energie. Vlivem kůrovcové kalamity musí zároveň více investovat i do výsadby lesů a zkvalitnit tak zemskou půdu, která se bude podílet na fotosyntéze.

Zároveň je potřeba dbát důraz na rychlý přechod k obnovitelným zdrojům, jelikož rok 2030 se nezadržitelně blíží.

Výsledky simulace jsou pouze ilustrativní a vycházejí z vypočítaných proměnných. Jelikož pracujeme se zjednodušeným modelem je nutné brát výsledky simulace jako hrubý odhad.