Předpověď počasí
Název: Předpověď počasí
Autor: Tereza Plánková
Nástroj: Microsoft Excel 365
Metoda: Monte Carlo
Definice problému
Mladý pár bude mít během příštího roku svatbu. Nemohou se dohodnout, jaký termín je pro svatbu nejlepší. Oba dva se shodli na tom, že by si přáli, aby měli hezký počasí. Pod hezkým počasím si představují slunečný den, kdy teplota bude mezi 20-23 stupni (ne moc teplo, ne moc zima). A vzhledem k tomu, že chtějí mít svatbu venku, tak by byli neradi, kdyby pršelo nebo pouze chvilku, protože jsou pověrčivý - a na svatbě prší štěstí. Dále kromě data řeší také místo, kde je svatba nejlepší. Na výběr jsou tři místa – Praha, Jihlava a Liberec. Ona je z Jihlavy a přála by si svatbu tam, on je z Liberce a také by si přál svatbu ve svém rodném městě a Praha je místo, kde spolu momentálně žijí, oba pracují a poznali se zde během studia a jsou ochotní mít svatbu i tady.
Cílem simulace je zjistit, jaký den/období a místo je nejlepší pro konání svatby, aby byla podle jejich přání.
Metoda
Pro tuto simulace byla použita metoda Monte Carlo. Metoda Monte Carlo je vhodná pro výpočet nejvíce pravděpodobných náhodných hodnot dané veličiny za pomocí generování velkého počtu pseudonáhodných čísel. Program pro modelaci byl zvolený Excel.
Model
Data byla stažena z Českého hydrometeorologického ústavu. Konkrétně se jedná o průměrnou teplotu, denní úhrn srážek a denní úhrn doby trvání slunečního svitu v daném městě. Takže máme celkově 9 souborů (3 pro teplotu, 3 pro srážky a 3 pro sluneční svit). Každý soubor obsahuje informace ohledně roku, měsíce, den a dané hodnoty v tom dni. Teplota je ukazuje, průměrnou teplotu dne ve stupních celsiích, srážky udávají, kolik mm v daný den spadlo a sluneční svit udává kolik hodin ten den svítilo sluníčko.
Do modelu byly použity pouze data za poslední tři roky (2020, 2021 a 2022). Vzhledem k teplotě, kterou si pár přeje na svatbě, byly vyřazeny zimní měsíce. Předpokládáme, že 20–23 stupňů během ledna, února, října, listopadu a prosince nebude.
Dále v každém souboru byl vytvořen sheet pro jednotlivý měsíc, kde jsou pouze hodnoty pro ten daný měsíc. Na každém z nich už můžeme generovat náhodné Monte Carlo vzorky, které nám ultimátně dají celý obrázek toho, kdy chceme svatbu.
Před samotným modelováním byla potřeba zjistit pravděpodobnostní rozdělení. Průměrná teplota měla rozdělení normální a srážky a sluneční svit mělo rozdělení lognormální. Na základě rozdělení jsme potom zvolili vzorce v Excelu pro výpočet náhodných vzorků.
Průměrná teplota
Pro každý měsíc jsem si vygenerovala náhodné hodnoty pomocí vzorce =NORM.INV(NÁHČÍSLO(); PRŮMĚR($E$2:$E$94);SMODCH($E$2:$E$94)). Poté jsem si nastavila podmínku =KDYŽ(A(E2>=20; E2<=23);1;0). Dále jsem zjistila z výsledků podmínky pravděpodobnost, rozptyl a směrodatnou odchylku. Provedla 1000 iterací přes citlivostní analýzu. A z výsledků znova udělala pravděpodobnost, rozptyl a směrodatnou odchylku.
Srážky
Vzhledem k lognormálnímu rozdělení jsem postupovala jinak, než bylo popsáno u průměrné teploty. V první řadě si ze sloupce s hodnotami udělám vedle sloupec logaritmů hodnot pomocí vzorce =LN(D2), poté z těch logaritmů udělám hodnoty normálního rozdělení =NORM.INV(NÁHČÍSLO(); PRŮMĚR($E$2:$E$94);SMODCH($E$2:$E$94)) a nakonec tyto hodnoty umocním na exponent =EXP(F2). Podmínku jsme zvolila =KDYŽ(G2<0,2;1;0). Poté pokračujeme stejně jako u průměrné teploty – pravděpodobnost, rozptyl a směrodatná odchylka, citlivostní analýza a znova pravděpodobnost, rozptyl a směrodatnou odchylku.
Sluneční svit
Sluneční svit má stejně jako srážky lognormální rozdělení, proto postupujeme úplně stejně. Akorát podmínka byla zvolena =KDYŽ(G2>=13;1;0).
Výsledky
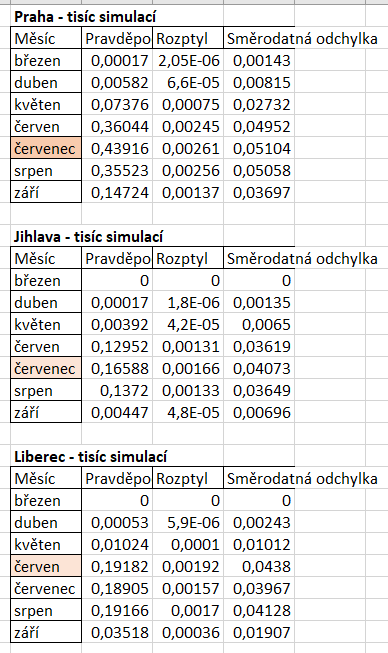
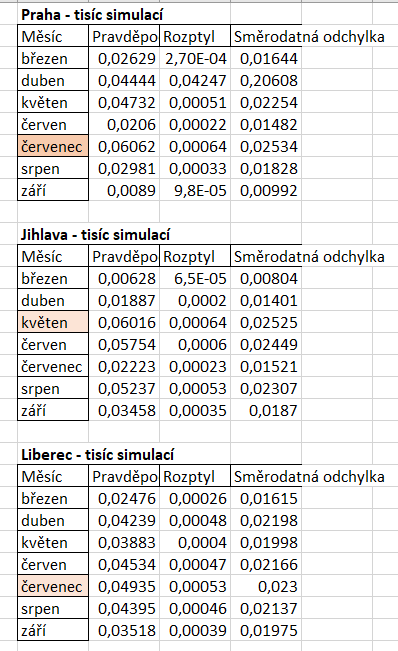
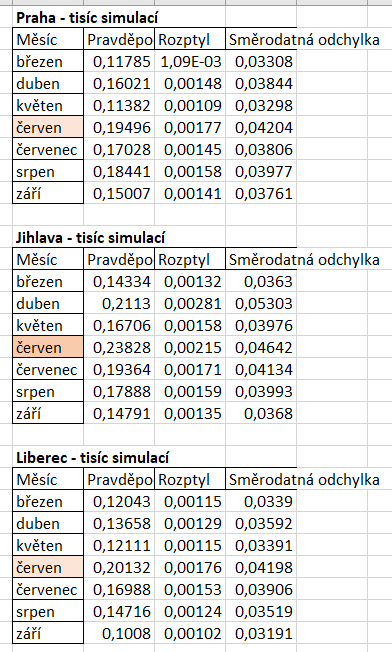
Parametry teploty, srážek a slunečního svitu jsou na sobě nezávislé, a proto byla simulace pro každou část provedena samostatně. Bylo provedeno 1 000 iterací. Následně se výsledky všech měsíců daly dohromady a porovnaly mezi sebou. Na obrázku můžeme vidět, zvýrazněnou největší hodnotu v dané lokalitě a tmavší barvou je zvýrazněn nejlepší pravděpodobný výsledek ze všech. Z výsledků můžeme vidět, že nejlepší období a místo pro svatbu je červenec a Praha. Přestože u slunečního svitu není červenec v Praze vítěz. Když se podíváme na výsledky, tak i v Praze v červenci je vysoká pravděpodobnost, že bude dlouho svítit.
Že bude na svatbě teplota mezi 20-23 stupni bude s pravděpodobností 0,439161 v Praze, s pravděpodobností 0,165882 v Jihlavě s pravděpodobností 0,19182 v Liberci.
S pravděpodobností 0,06062 nebude v Praze v červenci na svatbě pršet. Pravděpodobnost minimálního deště v Jihlavě je 0,06016 a v Liberci 0,04935.
Sluníčko s největší pravděpodobností bude nejvíce svítit v červnu v Jihlavě, a to s pravděpodobností 0,23828. V Praze je to červen s pravděpodobností 0,19496 a v Liberci také v červnu s pravděpodobností 0,20132. V Praze v červenci se jedná o pravděpodobnost 0,17028.
Závěr
Cílem simulace bylo nalézt den nebo období, které bude nejvíce vyhovovat představě páru o jejich svatebním dnu. Cíl byl naplněn. Bylo zjištěno období, ve kterém by byla nejlepší svatba. Po porovnání všech výsledků nejlepším měsícem je červenec a místo Praha. Přestože u slunečního svitu nemá největší pravděpodobnost červenec v Praze, tak předchozí dvě hodnoty ano a pravděpodobnost sluníčka je v červenci i tak vysoká.
Při zjišťování, jestli je lepší první nebo druhá půlka v červenci, jsem došla k závěru, že bude počasí přibližně stejné. Hodnoty jsou velmi podobné. Proto je jedno, zda bude pár pořádat svatbu na začátku, uprostřed nebo na konci června.