Multiplayer games
Contents
Multiplayer games
Game theory analyzes mathematical models of decision making in conflict situations. A conflict is formed by several participants who make decisions according to their best interests, and the outcome is not dependent on a single participant’s actions but also depends on decisions made by other participants. In many cases these situations can be described and analyzed as two player games. This type of games have a very important role in game theory. However, in reality there are often more than two participants and the purpose of game theory is to find general concepts that can be applied onto real life conflict situations. Thus, according to the number of players, we may consider Two player games and Multiplayer games (also known as n-player games, many-player games, multiperson games). In order to be considered a game, a modeled situation must fulfill certain criteria: [1]
- There have to be at least two participants
- There is a conflict of interests between participants
- The player’s behavior implies some uncertainty as they have different options for their decisions depending on the decisions of other participants
- There are different outcomes with different payoffs
- All participants are familiar with the rules of the game
Multiplayer games share the same characteristics as two player games. What is more, they are well defined for n players. Unlike in two player games, in n-player games participants may communicate and come to some agreements. If there is a possibility of negotiations prior to the start of the game, players may form coalitions and agree on strategies which are more beneficial for the cooperating players. Such games are called cooperative or coalition games. By contrast, games where participants cannot make preliminary agreements and form coalitions are called non-cooperative. All zero-sum games may be viewed as an example of non-cooperative games. As for cooperative games, forming a coalition for voting, in order to make decision, which can satisfy the interests of the participants is an example of such game. [2]
Non-cooperative n-player games
In non-cooperative games, the participants make decisions simultaneously and independently from each other. Players are looking to maximize their payoffs, therefore the goal is to find a strategy where no one would be better off if he chose to deviate from this strategy. [3] Mainly, such situations are described as two-player games, as it is easier to analyze the conflict on a model with less participants. However, these situations may as well be generalized for n players. For example, the N-player Prisoner’s Dilemma.
Auctions
In game theory auctions can be considered as a special type of multiplayer game. Theory of auctions is an example of successful application of game theory.[3] Auctions provide an alternative to the set price trade situations. There are several entities that participate in auctions : [1]
- Seller (sellers) has an intention of selling some commodity at a higher price
- Bidders are interested in buying a commodity at a lower price. A buyer is a bidder who wins the auction.
- Auctioneer is an entity or a person responsible for organizing the auction
The conflict of interests between the seller and buyer, as well as competition between bidders, create conditions for analyzing auctions within game theory. Furthermore, for each type of auction there are specific rules that define how the process of bidding is conducted and what requirements should be fulfilled in order to become the winner. In addition, not all auctions are organized with intention of selling some commodities: roles of buyers and sellers can be reversed, and the goal of sellers is to make a purchase at a lowest price. These auctions are called reverse auctions. [2]
Types of auctions
Auctions can be divided into categories based on their properties: [1]
- By bidders accepted in the game: In open auctions bids are accepted from anyone, in closed auctions bids can be placed only by bidders who meet specific requirements.
- By bids secrecy: In sealed-bid auctions (also known as envelope auctions) bids are placed privately and the value of one’s bid is unknown to other bidders. In open-cry auctions bids are voiced or submitted by other medium so that they are known to other participants.
- By the number of objects for sale: in single-object auctions it is possible to sell only one object per auction cycle, while multi-object auctions allow to sell multiple objects at once.
- By the price: first price, second price; decreasing or increasing price
According to typology offered by Ken Binmore in his book Playing for Real : A Text on Game Theory, we can distinguish different formats of auctions. [3]
- Take-It-or-Leave-It Auctions, also known as “Buy it now” on the Internet auctions. Here the price is already given and potential buyer has an option to pay the price or leave the auction.
- First-Price, Sealed-Bid Auctions. This type of auctions is standard for government tenders.
The bids are submitted privately in envelopes or via other secure medium. Then the highest bidding price determines the winner, who has to pay the price he submitted. It is assumed that in case of ties the winner is chosen at random.
- English Auctions. This type of auctions is probably the most famous, the one that often comes to mind when the term “auction” is mentioned. This is the kind of auction typically used for sales of antiques and objects of art. In this auction the price is increased by bidders. The bids are usually oral, the price may be raised in certain increments. Bidding continues until there are no more bidders willing to pay a higher price than the last bid. The last and the highest bid wins and the object is sold at that price.
- Dutch Auctions. Unlike the English auctions, the price in Dutch auction is decreased. This auction starts at the highest price set by the seller. Next, if nobody is willing to buy the commodity at that sum then the price is lowered. The first bidder to accept the new price becomes the winner of the auction. Dutch auctions usually have a short time frame, as they are commonly used for commodities that are perishable and need to be sold quickly, for example flowers, fish etc. However, sometimes this type of auction is also used for durable goods, in that case the period between separate price cuts can last for months.
- All-Pay Auctions. In this auctions the price is increased and the highest bidder wins in the same way as in English auctions. However, unlike in other types of auctions, every bidder has to pay the sum he submitted, even if they didn’t win the auction. Bribery is an example of all-pay auction: every participant pays in secret, in the hope of being the highest bidder.
- Vickerey Auction (second price auction). Named after its author, the Nobel-prize winning economist William Vickerey, this is a sealed-bid type of auction where the highest bid defines the winner. What makes Vickerey auctions stand out is the fact that the winner does not pay the price he submitted but the second highest price. Vickerey auction has its advantages for sellers: while in first-price auctions bidders have to take into account many complex factors, such as the number of players and their potential bids, they also tend to bid lower, as their bid reflects the sum they would have to pay, and their goal is to minimize that amount. In Vickerey auctions they don’t need to pay the amount submitted in their bid, but the second highest bid. At the same time, bidders still want to minimize the price they have to pay. As a result, it only makes sense for participants to bid the exact amount at which they evaluate the commodity, while in first-price auctions they tend to bid lower.
A similar principle to Vickerey auction is often used by Internet auctions, such as eBay. The bidder submits the highest amount he’s willing to pay. If the bid surpasses previous bidder’s maximum, he becomes the current winner until someone else beats his highest bid. However, the current price takes the value of the previous bidder’s maximum bid (the second highest price), while current winner’s maximum (the first price) stays hidden. If no one else bids more than his hidden highest price, he wins the auction. The difference between Vickerey auction and the described auction is that the latter may have more than one iterations – a bidder can be overbid and place a higher bid in the same auction again. In addition, the same goods in which a bidder is interested, may be sold in multiple auctions. That may require some changes in strategy.
Winners may sometimes find themselves dissatisfied with the outcome of the auction if the actual price they payed seems to be higher than the value of the goods (whether real or just in their perception). In auction theory there is a term for this situation - the Winner’s curse. For that reason, players are most likely to avoid this situation in Vickerey auction, as they tend to make their bids based on the true value.
Admittedly, the above list of auction formats cannot be considered complete. Some types of auctions are less common and well-known. Auction theorists strive to design new concepts for auctions based on specific requirements. For instance, Japanese auction (which can also be considered a sub-type of English auction) is worth mentioning. Japanese auction is similar to English auction in that the bids are made in an open manner, the price is rising in increments and the bidder who offered the highest price wins and pays that price. The difference is that all participants who are willing to pay the price have to show it from the beginning, usually by raising hands. If the bidder puts his hand down that signifies that he does not want to pay the price and no longer participates in the auction as a bidder. In other words, the amount of competitors is known throughout the whole auction. By contrast, in English auctions someone can bid when the auction is approaching its end even if he did not show any interest while the price was lower. [2]
Cooperative games
In many real conflict situations the participants may communicate and form some coalitions. While in antagonistic games a player cannot have any advantage if he decides to deviate from the equilibrium, in these cases multiple participants may benefit from forming a coalition rather than from what their payoffs would be if they decide to remain in the equilibrium state on their own. At the same time, cooperation may also cause conflicts between participants as each player’s goal is to receive the highest possible payoff. For that reason it is important to analyze whether a coalition should be formed and if so, under what conditions. The optimal formation of coalitions is still considered to be one of the difficult problems in game theory. However, forming a right coalition may result in a payoff that would not be attainable by each player individually.
In cooperative games it is not always necessary to form coalitions in a sense that players but do not need to redistribute their payoffs .[4]
In case of coalition games, there is a necessity to redistribute the income between players. Of course it is possible to divide it equally. However, this option may not always be fair considering each player’s contribution, nor optimal in terms of maximizing their potential payoffs.
Example 1. [5]
There is a street band consisting of three members: Alex, Bob, Cameron. Alex sings, Bob plays the guitar and Cameron plays the drums. Together they earn 30 euro per hour. The problem is, how to divide these earnings between the members? First option is to divide this sum equally . But what if such solution does not reflect the contribution of each member? Let us suppose the members also tried playing solo and in sub-units. In that case their earnings would be the following:
| A | B | C |
| 10 | 5 | 3 |
| AB | AC | BC |
| 22 | 15 | 10 |
With this information, the members would not agree to receive any less than they would have if they played solo, but also not less than if they were in any of the sub-units. At the same time, playing as a three-member band is still more beneficial than playing in sub-units as the payoff is larger. Thus the distribution of payoffs has to satisfy the condition:

If the payoffs satisfy the above condition, the members would agree with such distribution of payoffs. Therefore this set of solutions is stable and is called the core of the game. Any particular solution from the core would be acceptable. If it is impossible to satisfy all the conditions, then the core is empty, meaning there are no stable solutions to the game.
Evolutionary game theory
At present, one of the rapidly developing branches of game theory which involves multiplayer games is evolutionary game theory. This theory is based on the expectation that the most successful behavior will dominate the way it does in biological evolution. Unlike classical game theory, where players are supposed to be rational, in evolutionary theory players are assumed to be acting without understanding how their decisions may affect and inform the decisions of others. Evolutionary game theory studies populations of players, their interactions and the overall development of the state of the system. The inclusion of multiplayer games into evolutionary game theory takes into consideration non-linearities and helps with the modeling of the more complex systems. [6]
There are parallels between Evolutionary Game theory and Cooperative game theory. These connections are investigated in the Evolutionary Nash Program. [7]
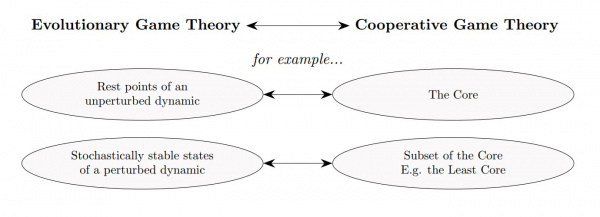
Application of evolutionary game theory is not limited to biology, but also includes sociology, economy and any other field that studies development of patterns of behavior in time. For example, the problem of pricing where a population of buyers decide which goods they will buy, or the impact of employees’ decisions on organizational culture and so on.[6]
References
- ↑ 1.0 1.1 1.2 MAŇAS, Miroslav a Martin DLOUHÝ. Games and economic decisions. 4., přeprac. vyd. Prague: Oeconomica, 2009. ISBN isbn978-80-245-1610-3.
- ↑ 2.0 2.1 2.2 DIXIT, Avinash and Susan Skeath, 2004, Games of Strategy, 2nd ed. New York: W.W. Norton. ISBN 978-5-00057-311-2.
- ↑ 3.0 3.1 3.2 BINMORE, K. G. Playing for real: a text on game theory. New York: Oxford University Press, 2007. ISBN isbn978-0-19-530057-4.
- ↑ R. Aumann. Subjectivity and correlation in randomized strategies. Journal of Mathematical Economics 1 (1974) 67–96.
- ↑ SAVVATEEV, Alexey. Game Theory. Lecture 35. Cooperative game theory - subway musicians. (in Russian) [online]. [cit. 2019-01-31]. Dostupné z: https://www.youtube.com/watch?v=R7WYDMQVAVU
- ↑ 6.0 6.1 NEWTON, Jonathan. Evolutionary Game Theory: A Renaissance. Games [online]. 2018, 9(2) [cit. 2019-01-31]. DOI: 10.3390/g9020031. ISSN 2073-4336. Dostupné z: http://www.mdpi.com/2073-4336/9/2/31
- ↑ Gokhale CS, Traulsen A (2014) Evolutionary multiplayer games. Dyn Games Appl 4(4):468–488