N-player prisoner's dilemma
Contents
Introduction
You have already become familiar with Prisoner’s dilemma. But now imagine a different situation. What if there are three prisoners. And even worse, what if there is a lot of them. How will they behave? What strategy will they use. They can cooperate or they have to make fools out of the other. Sometimes though, the environment is shared and not cooperating can have devastating consequences. Imagine a field, a pasture for cattle. There are three farmers who can send their cows on this field. But as there are more and more cows on it, it becomes devastated. Each farmer sends their cows until the field is totally ruined. That is a classical dilemma of this topic. In this chapter you will find out more details about how n-player prisoner’s dilemma works and how is it solved.
Problem definition
N-player prisoner’s dilemma is a multiplayer game from Game theory. It is a expansion of classical Prisoner’s dilemma, because its lack of applicability. In real world problems, there usually are more than two players or two sides of an argument. Some of these problems can be turned to two-player games, but there are some you cannot. These situations are called N-player games or Multiplayer games.
Interesting fact: In group of 8 players there are 28 one-to-one relations. There are 40.320 potential relationships (8!, groups of 2,3,4,5,…). But in group of 50 players there already are 1225 one-to-one relationships.
Multiplayer games like N-player prisoner’s dilemma have 3 defining properties, which are similar to the characteristics of regular 2-player prisoner’s dilemma.
- Each player can either cooperate or defect
- Defecting is usually dominant strategy for each player
- The dominant strategies intersect at a deficient equilibrium point
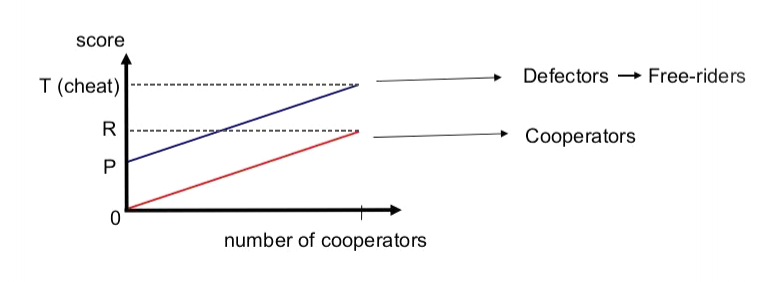
What it really means is, that all players want to make their utility higher, therefore they usually incline to defecting strategy. Regardless of what the other players do, each one receives a higher payoff for defecting behavior than for cooperating behavior. But because of limits of the environment equilibrium is usually deficient. We don’t find true Nash equilibrium. All players receive a lower payoff if all defect than if all cooperate. The dominance of the non-cooperative strategy over cooperation, regardless of the overall share of cooperating entities, shows the mutual position of the curves of the functions of cooperation and non-cooperation in the graph. The specific form of function curve depends on the concrete problem’s definition. [1][2]
Parameters
Beside of defecting strategy, we can find more parameters describing situation and decision making of players. (In game theory in generally we call them agents, as it could be individuals, groups, companies, artificial agents or imaginative organization structures).
Information – agents can either know how others make their decisions, what are their biases and limits, or not know. They can also have or not have information about environment (e.g. limits of pasture)
Time – Decisions agents make can be proceeded simultaneously or in turns. Also, one’s turn can take longer than others, leading to overlaying of turns (one can make two changes in their strategy while the other will only make one change). The game itself can be played only as one interaction or iteration, or as repeated game. This repetition could be certain number, or it could be infinite. If game is infinite again information about it will be very important for decision making
Communication – If agents can communicate among themselves, they can form fellowships and coalitions for improving their results. Goals – With postmodern emancipation we can assume that some agents come into a game with different goals. Therefore, their rational behavior towards their personal goal could be different from others.
Space – In todays world of fast travel of information, space doesn’t make too much of a difference. But information is not the only thing traveling through space. We can find more spatial problems and definitions than just that. These afterwards create limits for players and their decisions. Often when space is bigger than agents in it, they can move in it, having influence on ever changing environment
Participation – Huge difference for agents is not having to participate. It can refuse to participate in whole game or in some of iterations. For example, in chess you can’t refuse to move, on the other hand, Kutuzov beat Napoleon by avoiding battles.
Personalities of agents – last mentioned parameter will be personality of agent. Everyone is different and can decide differently then others when faced the same situation. We will introduce personalities as Szilagyi[3] described them. He presents 4 areas of distinction. Need to say, that “personalities” as we understand them here, will be just decision approaches, that can be designated as the most usual ones.
Firstly, distinction he used for his work model[3].
- Pavlovian personality – means that agent, internally, changes probability of repeating the same decision by amount of reward or penalty coming from this decision. How fast he learns from previous wins or loses is called “learning rate”. This personality is derived from experiments of I.P. Pavlov on dogs and Thorndike’s Law of effect.
- Greedy – agent will act same way as any of his friend or foes, who got the best result
- Conformist – agent will act the same way as majority of other agents
- Accountant – agent with this personality will count average payoff or utility of previous decisions and decide by that
- Statistically “predictable” – has a constant parameter “p” – cooperation. Short-time rational agent always defect (p=0), Altruistic agents ignore short term interest and cooperate (p=1), P=0.5 acts randomly, agent is totally unpredictable.
Secondly, Big Five approach to personalities, Szilagyi used this distinction in his standing ovation study
- Openness
- Conscientiousness
- Extroversion
- Agreeableness
- Neuroticism
Third, approach that distinguishes what kind of action will agent perform after result.
- trustworthiness (probability of choosing cooperation after reward for cooperation by all members)
- forgiveness (probability of choosing cooperation after “sucker’s payoff” – when cooperating while the opponent/s was defecting)
- repentance (probability of choosing cooperation after “temptation payoff” – when defecting while other one/s cooperating)
- trust (probability of choosing cooperation after receiving punishment for defecting by all members)
Last approach probably the most particular one, personalities defined by 16 mental disorders. These disorders are extremes of regular people’s personalities, therefore combination of them puts together agent’s personality. Traits and disorders are shown in following table.
| Adventurous (Antisocial) | Self-Confident (Narcissistic) |
| Aggressive (Sadistic) | Self-Sacrificing (Self-Defeating) |
| Conscientious (Obsessive-Compulsive) | Sensitive (Avoidant) |
| Devoted (Dependent) | Solitary (Schizoid) |
| Dramatic (Histrionic) | Vigilant (Paranoid) |
| Idiosyncratic (Schizotypal) | Exuberant (Cyclothymic) |
| Leisurely (Passive-Aggressive) | Serious (Depressive) |
| Mercurial (Borderline) | Inventive (Compensatory Narcissistic) |
All these parameters can be found in regular two player prisoner’s dilemma, but in N-player versions, especially personalities have significant value, as there is more players and more types of situation and more interactions are about to arrive.[3]
Models
As it is very difficult to create a matrix like one in two player game, we need to choose another approach to modelling. In three-player game you would need 3x3x3 matrix, in game of 4 players 4x4x4x4 and so on. It would be almost impossible to make even like 10-player game. Therefore, we need to replace matrix approach. We will use something like the first graph. At first, we will infer 2-player graph out of 2-player matrix.
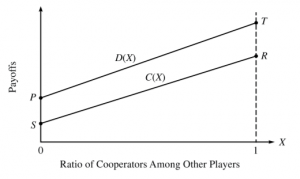
The letters describe something we already mentioned in previous part. “P” – means punishment to an agent when all agents defect. “R” – means reward to an agent when all agents cooperate. “T” – is temptation’s payoff, it is a utility/reward for agent when defecting while others cooperate and last letter “S” – sucker’s payoff, utility/reward or punishment for cooperating while others defect.
In this graph we can easily replace axis x – second player’s choice with ratio of cooperating agents in the rest of the group. This way we can apply graph on any size of a group, even again on two-player game. Last adding to the graph will be connecting point P with point T – creating “defectors’ payoff function” (D(X)), and also connecting letters S and R – creating “cooperators’ function” (C(X)). These function can have various shapes, don’t have to be linear, and can also go below zero. Look on this graph here:[3]
Examples
Probably the best-known example of n-player dilemma is, already mentioned, problem with cow pasture – Tragedy of the commons . It is inspired by real situation that happened in 18th century in England.[4]
Imagine situation, six farmers share common field, a pasture. Each farmer takes on the pasture one cow every day. If this cow is well fed it will weight 500kg. The pasture can hold up to six cows, if there’s more it will be overgrazed. So, if more cows are added, they will be starving, and the weight of each animal will be lowered by 50 kg. Being a farmer, you want to add more cows, (900kg – 2x450kg > 500kg). Everyone of these farmers are adding more cows, making it dominant strategy. In the end, adding more cows will totally deteriorate and no cows can live there. This problematic dilemma describes situation of merely all environmental issues in todays world. What could governments do about it? They can either privatize the field – sell it to one owner, so he can add as many cows as he wants at his own risk, or they can setup regulations (how many cows can each farmer have). This way cheaters are punished by government and not the environment. There is a certain conspiracy about this problem, because it was published in time of beginnings of privatizations of properties in US and it was taken as a campaign for it. More about this dilemma here. There are many similar examples like water usage, waste dumping etc. [5][6]
Another example of n-player dilemma is called Unscrupulous diner’s dilemma. Imagine you go on a dinner with 3 friends, before ordering your food you decide that you split the bill equally. However, there are two types of burgers in the menu, regular one (utility of 1) and XXL one (utility of 2). Prices of those burgers though are not adequate to the utility. It is 1$ for regular one and 3$ for XXL one. My dominant strategy would be to eat as much as I can and pay less. So, I will order XXL burger and let others pay for me. Therefore, total amount paid will be 6$ (3+1+1+1) and I will pay just 1.5$, but I will receive 2 utility / you get 2 times better burger but only paid 1.5-time the money. However, everyone of your friends think the same way, each one of them wants to have twice as much burger at just a little bit more price or at least, nobody wants to pay for the douchebag ordering the big burger while being stuck on the regular one. So, in the end everybody orders XXL burger – bill is 12$ and everybody pay 3-times more but only get twice better burger.[7] .
Problems like these are sometimes called “freeriding” or “freeriding problems”. One member of the group uses it to gain utility, but if everybody in the group would acts the same way, everyone would lose more than gain. N-player prisoner’s dilemma is in general sociocultural issue. Individual rationality leads to collective irrationality. It presents modern battle between individualism and collectivism. On the other hand, there is also few examples, showing otherwise.
First one is called Volunteer’s dilemma game. It models for example meerkat behavior when being on guard. One member of a group chooses between making a little sacrifice in name of bigger good of the whole group or just wait until somebody else does the sacrifice instead. Mentioned meerkats take on themselves roles of sentries even though when they warn about incoming danger, they face immediate thread of dying because of being discovered first while calling a warning. This dilemma is often connected with Bystander effect and other psychological effects discovered in 1960s and 70s by Milgram and Zimbardo.[8]
Imagine you and your family want to go for a dinner. The restaurant is quite far away, and you would rather stay at home and have dinner there instead of that long drive. But you think that don’t want to be the bad guy who ruins dinner for everybody, so you go. Now imagine, that every member of the family thinks just the same way. And with lack of communication you all end up going to the restaurant, even though nobody truly wanted to go there. This is called Abilane Paradox, because of example with restaurant in town of Abilane. It’s quite the opposite we see in previous dilemmas but, it fills up the overview about decision-making. [9]
Practice
Try to solve this N-player game:
- 6 players are waiting to get checked into a flight.
- The consumers utility is based on when they get checked in:
| Order served | Utility |
|---|---|
| 1 | 20 |
| 2 | 17 |
| 3 | 14 |
| 4 | 11 |
| 5 | 8 |
| 6 | 5 |
- The airline will check people randomly if no one is in line, but those in line will be checked-in first
- Players incur a 2 units loss of utility by waiting in line.
- What is the equilibrium number of people standing in line?
Results: 4 people standing in line - The 5th guy gets 6 Utils guaranteed by waiting, but a 50/50 of getting 8 or 5 (average 6.5) Utils if he takes a seat. The -3 for getting picked last vs the -2 for waiting in line for 5th is more than made up for by the chance he gets picked 5th anyway for +2. The 4th guy isnt so lucky. The average of being picked 4/5/6 is only 8, while standing in line guarantees 9. [10]
References
- ↑ Cooperation in n - player Prisoner’s Dilemma threshold game Boza, G. (1,4) , Könnyű, B. (1) and Számadó, Sz. (2,3) 1-Department of Plant Taxonomy and Ecology, Eötvös Loránd University 2-HAS Research Group of Ecology and Theoretical Biology, Eötvös Loránd University 3-Collegium Budapest, Institute for Advanced Study Budapest, Hungary 4-IIASA, International Institute for Applied Systems Analysis Laxenburg, Austria
- ↑ Bach, LA, Helvik, T & Christiansen, FB 2006, 'The evolution of n-player cooperation—threshold games and ESS bifurcations' Journal of Theoretical Biology, bind 238, s. 426-434.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Szilagyi, Miklos N. "An investigation of N-Person prisoners' dilemmas." Complex Systems 14.2 (2003): 155-174.
- ↑ Morgenstern, O. Theory of Games and Economic Behavior; Wiley: New York, NY, USA, 1944. 3. Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982.
- ↑ G. Hardin, “The Tragedy of the Commons,” Science, 162 (1968) 1243– 1248.
- ↑ N-Person Prisoner's Dilemma. Stanford.edu [online]. [cit. 2017-06-09]. Dostupné z: https://cs.stanford.edu/people/eroberts/courses/soco/projects/1998-99/game-theory/npd.html
- ↑ Glance, Natalie S.; Huberman, Bernardo A. (March 1994). "The dynamics of social dilemmas". Scientific American
- ↑ Poundstone, William (1993). Prisoner's Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb. New York: Anchor Books ISBN 0-385-41580-X.
- ↑ Harvey, Jerry B. (1988). The Abilene Paradox and Other Meditations on Management. Lexington, Mass: Lexington Books. ISBN 0-669-19179-5
- ↑ Matthew Rousu 2014, Game Theory N person games, available at https://www.youtube.com/watch?v=GxCWuktSckQ [22.1.2019]