Carsharing Fleet Optimization
Introduction
Recently, carsharing becomes more and more popular in large cities. Short-term rental (from several minutes to 24 hours) of a car with possibility to drop it anywhere in the allowed area in the city attracts people who, for some reason, do not want to use their own vehicles. However, it is not always convenient. If the fleet is relatively small, the probability that a car will be somewhere close by is also quite low. Cars also must be refueled or recharged sometimes by staff, which would increase cost of the fleet maintenance with increasing of the fleet size.
Problem definition
Carsharing companies have to solve a problem of optimization of their fleet size, which is not simple. The entire system of carsharing is complex and has many different parameters that must be considered for decision making. For example, if the number of cars available in the city is relatively small the maintenance is also respectively inexpensive. However, in this case, the probability that users can find a car next to their location drops drastically. On the other hand, having too many cars leads to the risk that they will stay with no use for long time. The goal of this simulation is to understand how the carsharing system behaves and propose quantitative solution on optimal number of cars and price of rent to maximize marginal profit of a hypothetical carsharing company.
Method
Since the system consists of several entities, each of them is able to some extent to make decisions, and system itself is dynamic and requires to take into account spatial factors, agent-based modelling was chosen as the most appropriate tool to design the simulation. Implementation was performed using NetLogo software platform.
Model
The model is represented by several agents and accepts some simplifications. It is assumed that the simulation will be run on ticks, every tick represents one minute of real time.
Agents
The model contains 3 types of agents: cars, users, and maintainers.
Cars
Represent the vehicles used for short-term rentals. Cars have the following characteristics:
- price - cost of rental per minute
- status - current status of the vehicle, can be idle (the car is ready for rent), booked (the car is booked but paid rent has not started yet), in rent (the car is taken in paid rent by some user, for the purpose of this simulation it means that the car is moving), needs maintenance (the car is not visible for users but visible for maintainers), and out of service (the car is not visible for users and maintainers, is already under maintenance by one of the maintainers)
- fuel - how many liters of gas is left
- mileage - for how many kilometres the car was already driven, every car must go through maintenance procedure every 10,000 kilometres
- premium - boolean parameter that indicates if the car belongs to premium class
- inspection - boolean parameter indicating that the car needs to undergo an inspection.
Cars are located in the simulation space and, if possible, can be rented by users. Users can drive cars, i.e., move it from one point of the simulation space to another. Cars can be re-fueled and taken to inspection by maintainers. It is assumed that a car can serve for the purpose of carsharing only for 100,000 km, then the car is replaced with absolutely identical one.
Users
Represent people holding a driving license, registered in the carsharing service and actively using it. Every tick of the simulation users decide with probability 1% whether they want to travel from the current location to somewhere else and, if so, to what coordinates of the simulation space. However, there are peak hours when most of users want to travel (for example, commute to work). It is assumed that there are 3 such hours every workday, 15 hours during the week, i.e. 9% of all the time. During these hours 50% users want to travel somewhere.
Then, user starts looking for a car and, if the user finds one near by, decides if he or she wants to book it. The closer the car and the lower the price of the rent, the greater is probability that user takes the car. If user decides to rent a car, the user first books it and walks to the car. Then, user decides whether the user wants to start rent. With probability 1%, user who booked a car will decide not to start paid rent for some reason (for example, the car is dirty). When user decides not to take a car or not to start paid rent, it is assumed that the user gets to the destination point by personal car or by public transport. In the end, user who decided to travel travels anyway, by car or without it. If user travels by car, the user leaves the car exactly at the destination point. Users have the following parameters:
- travel - boolean parameter indicating if user is travelling at the moment
- destination (destinationx and destinationy) - destination where user is travelling to (applicable only if travel = True)
- car_assigned - car which user uses for travelling, could be Nobody if user travel not using a carsharing car (applicable only if travel = True).
For every user, maximum acceptable time of walking to the car before booking is 20 minutes (2 km).
Maintainers
Represent employees of carsharing company who are responsible for maintenance of the cars. They have their own vehicles (not the agent cars) and identify the cars which need maintenance in the simulation space based on the car's parameter status. The identified car is marked as out of service until maintenance is over. It is assumed that as soon as maintainer reaches the car, maintenance is done and car is again ready for rent. Maintainers have the only parameter - car_assigned - indicating the car assigned to them for maintenance (could be Nobody if no car is assigned). There are only two conditions when a car can be marked as needed maintenance:
- fuel level is below 2.5 liters (for this simulation, it is number close to amount of fuel needed to drive across the square simulation space diagonal)
- car exceeded another 10,000 km and requires inspection.
Simplifications
Since the carsharing system is very complex, for the purpose of this simulation some simplifications were accepted.
Space
Space of the simulation is considered uniform, i.e., there is no roads, buildings, and traffic in the simulation space. It does not matter what roads the users will drive across and how much time they will spend in traffic. On the other hand, what matters is duration of rent, which for this simplification does not depend on the traffic. The city is assumed to be of a square size 20×20 km. The simulation field is set of size 100×100 patches, which means that every patch has height and width equal to 200 m (0.2 km).
Prices
In real life, carsharing companies often offer different plans. It is normally fixed price per minute (usually depending on current demand) and packages with different duration with or without included mileage (for example, 2 hours of rent with 20 km included with fixed price per minute and per km after exceeding the included amount of time and mileage). For this simulation, only fixed prices per minute are available. The reason is that, even though some carsharing providers offer a wide range of different packages and plans, in the end final price does not differ much for each of the package.
Cars
There are several simplifications related to the cars.
- First, all of them have the same fuel consumption: 7.5 l per 100 km. It means that 1 liter of fuel will cover approximately 13.33 km.
- Second, it is assumed that cars do not need any maintenance except for regular inspection every 10,000 km and re-fueling.
- Third, only users can drive the cars. It is assumed that maintainers do no move the cars (which could happen in real life to adjust the car locations to expected demand) and perform inspection every 10,000 km at the place where the car is located at the moment
- Finally, there are only 2 types of cars: regular and premium, they have totally identical characteristics, only price differs.
Users
All the users drive cars with the same speed, 40 km/h. All of them are very careful and never have any accidents. Users drive cars only from one point in the simulation space to another, they do not drive between several points and do not leave the rent on pending (in real life, for example, some people could take a car to go for groceries and back and leave the car parked in paid rent while shopping). Without a car, users walk with the speed of 6 km/h.
Revenue and expenditures
Since the goal of the simulation is to find optimal parameters to maximize marginal profit, a task of financial calculations appears. However, calculations in the simulations are very simple. For the purpose of this simulation, Czech crowns were used as currency for all the financial operations. There is only one way to increase revenue - by renting out the cars. There are several expenditures:
- fuel price (added after every refueling, by default 30 CZK per liter)
- inspection cost (added for each car every inspection, assumed to be equal to 15,000 CZK)
- cost of maintenance, including salary of maintainers, fuel for maintainers' vehicles, and so on (by default 10 CZK per minute).
Margin profit is calculated as revenue minus expenditures minus initial expenditures. Initial expenditures include the price of the cars. It is assumed that regular car price is 400,000 CZK and premium car price is 800,000 CZK.
Results
The simulation is designed in a way that number of cars, number of users, number of maintainers, number of premium cars, rental price for normal and premium cars, fuel price, and maintenance rate are adjustable.
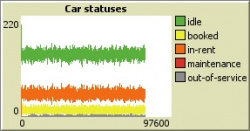
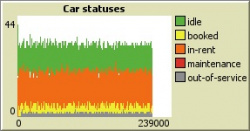
Unfortunately, it was not possible to get actual data from a real carsharing company operating in Prague. However, according to publicly available observations in the carsharing operator's application, ratio of cars available for rent is in average 70-80%. Similar results were obtained for 1,000 users and 200 cars (5 users per car).
It is visible that the results are stable and fluctuations in numbers of cars of each status are within narrow boundaries. Thus, the simulation is considered to be developed well.
Further in this section, different ratios of users per car considered, all the observations are listed. Since a tick of the simulation is counted as 1 minute of real time, in each case the observation period was set as one quarter (around 131,000 ticks).
Normal ratio
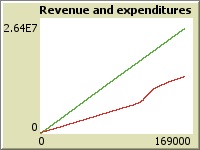
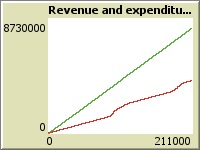
With normal ratio (5 users per car), results look fine, revenue exceeds expenditures twice. Return of investment may happen already in 3 years, which is okay. However, cost of maintenance starts growing faster closer to the end of the quarter since there are some delayed expenses such as planned inspections. However, this scenario looks good in general and will be used for comparison for the future cases.
Another important observation here is that with 5 maintainers, almost no cars are in the maintenance state, which means that maintainers manage to work on the car as soon as it needs maintenance.
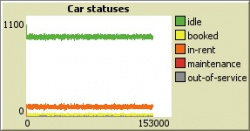
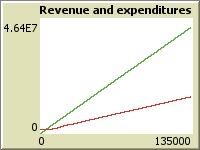
High number of cars
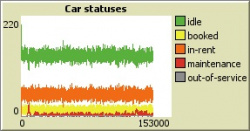
In this scenario, number of cars was increased to 1,000 (including 145 premium ones) and was equal to number of users. As a result, 85-90% of cars were in idle state all the time. But it positively affected profit: now revenue exceeds expenditures three times. Also, the curve of expenditures looks more stable: every car has less mileage and requires less investments. However, considering that initial investments are significantly higher, since number of cars is 5 times greater than in previous scenario, and return of investment would take almost 40 years. Also, for the period of one quarter with such number of cars, expenses on inspections and car replacements are not yet visible on the graph and will be higher (which means smaller gap between revenue and expenditures) in the future.
Hence, it makes no sense to increase number of cars that much because margin profit in the end will be much worse than in case with 200 available cars.
Low number of cars
For this simulation run, 40 cars were left including 12 premium ones. At the same time, it makes no sense to keep 5 maintainers for such a low number of cars and only 1 maintainer was kept. Because of low number of cars, statuses fluctuated more. However, number of idle cars still exceeds number of cars in rent: users are not eager to rent a car because it is mostly far away from them. Due to lower cost of maintenance, revenue is still almost twice greater than expenditures and, due to lower initial investments, return of investments will happen already in 1.5-2 years.
Extremes
Two extreme scenarios were also tried: 4 cars (including one premium) with 1 maintainer and 10,000 cars (including 1,450 premium ones) with 5 maintainers for 1,000 users. In the first run, revenue barely exceeded expenditures, return of investments would take decades. In the second run, until the end of the quarter, revenue value did not even reach the value of expenditure.
Optimization of the best scenario
Last runs of the simulation aimed to increase margin profit by decreasing number of maintainers and slightly increasing number of cars comparing to the best scenario (200 cars per 1,000 users). It turned out that even one maintainer is enough to perform routine maintenance of the fleet. Number of cars waiting for maintenance grew but the profit in the end increased. Graph of car statuses looks similar to what was shown before with a extra red ("need maintenance" status) cars. On the other hand, revenue now exceeds expenditures 2.5 times (comparing to 2 times with 5 maintainers). It means that return of investments may happen already in 1.5-2 years.
At the same time, increase in number of cars from 200 to 250 (with 1 maintainer) kept the ratio revenue / expenditures at the same level increasing turnover. However, considering greater initial investments, return of investments would happen definitely not sooner than with 200 cars.
Conclusion
Two optimal sizes of fleet size were discovered:
- few cars (about 25 users per one shared car) - due to relatively small initial investments and revenue significantly exceeding expenditures, return of investments for this scenario will be quite quick, in 1.5-2 years
- ratio mostly used by currently operating services (about 5 users per one shared car) in combination with optimized maintenance costs - greater turnover and revenue, which is 2.5 times greater than expenditures, allows to achieve return of investments in the same 1.5-2 years.
Therefore, new carsharing providers before running their business may choose either of the scenarios based on their abilities to get the initial investments. Already established companies may adjust their user-per-car ratio to the nearest one by either attracting new users or increasing the number of cars in the fleet.