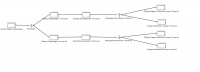
Covid-19 Mass testing in Slovakia (SIMPROCESS)
Contents
Assignment
- Simulation: Covid-19 Mass testing
- Author: pavm13 21:00, 20 January 2021 (CET) Milan Pavelčák
- Model type: Discrete simulation
- Used tool: SIMPROCESS
Problem definition
In Slovakia government decided to fight coronavirus by testing its population in a massive way. Such action requires a number of qualified personnel to be paid and premises to be secured. The goal of this simulation is to find an optimum (from the economic point of view and also from the personnel side) and decide how many sampling points need to be opened along with number of experienced personnel in order to test as many citizens as possible. Another point worth mentioning is that in this simulation population will be divided into two groups. First one will consist of people older than 60 years and the second one of peple between 15 - 59 years old. Reason for this division is to take care of older people and to protect them from the dangers posed by young asymptomatic citizens.
Flow of the simulation: Simulation will start with people coming to sampling points. Then they will be sorted based on their age into two groups (in simulation priority for sorting was used) and they would have to fill some paperwork and other staff. This requires one administrative worker and one police officer. Both groups will have their own administrative worker and police officer in order to keep them separated. After that citizens will wait in line for samples to be taken by qualified medical laboratory technician. After having their samples taken then they will wait again for the results which will be provided by another administrative worker and then sorted again according to the test result (for this in simulation data from webpage were used and probability of positive citizens was calculated). Citizens with positive result will have to wait again for instruction provided by another administrative worker and then they are free to go home to self-isolate. The rest, the negative ones will be given certificate and also free to go home.
Models
In this simulation 4 models with different conditions will be used:
- Model 1: The duration of the first model will be 4 hours with 8 sampling points evenly distributed for both groups. The variable according to which the number of sampling point is determined are the roles/resources.
- Model 2: In the second model duration of the simulation will be 8 hours and other conditions will remain the same as in Model 1.
- Model 3: In the third model 2 more sampling points for citizens below 60 years will be added and the duration of simulation will be 6 hours.
- Model 4: In the last model for this simulation duration will be set to 8 hours, sampling point for younger people will be set to 8 and for people older than 60 years number of sampling points will be set to 2.
Number of people to be tested
The data source is a page of a smaller city that has published the test results on its website. From this page, the numbers of test citizens were drawn, as well as the positivity of the tests performed. [1] Numbers of people incoming to the sample points to be tested was calculated as average from the data source and afterwards divided according to the demographic information about Slovakia. [2]
- Citizens over 60: 266
- Citizens below 60: 1544
Roles/Resources
As mentioned before economic point of view is also important for this simulation therefore each and every role will be seen as resource with allocated cost (hour wages)[3]. Due to the nature of SIMPROCESS features when it comes to working with resources roles were created for both groups:
| Role | Hourly wage (€) | Number required for one sampling point |
|---|---|---|
| Medical laboratory technician < 60 | 7.33 | 1 |
| Medical laboratory technician > 60 | 7.33 | 1 |
| Administrative worker < 60 | 8.98 | 4 |
| Administrative worker > 60 | 8.98 | 4 |
| Police officer < 60 | 12.74 | 1 |
| Police officer > 60 | 12.74 | 1 |
Waiting times
Incoming intervals of people coming to the sampling points to be tested was calculated with Poisson distribution for both groups. For waiting which can be found in multiple parts of the process Exponential distribution with various means was used.
Results
Model 1
As already mentioned, the duration set for first model is 4 hours and the simulation will take place in one day between 8:00 - 12:00. After 12:00 there will not be a chance for citizens to enter the sampling point. However, for those who will be still inside a sampling point there will be 30 additional minutes. Number of sampling points in this model is 8.
| Group | Total generated | Remaining in system | Processed |
|---|---|---|---|
| Below 60 years | 1550 | 1462 | 88 |
| Over 60 years | 293 | 13 | 280 |
| Resource | Idle | Busy |
|---|---|---|
| Medical laboratory technician < 60 | 1,340% | 98,660% |
| Medical laboratory technician > 60 | 14,873% | 85,127% |
| Administrative worker < 60 | 0,302% | 99,698% |
| Administrative worker > 60 | 43,749% | 56,251% |
| Police officer < 60 | 0,741% | 99,259% |
| Police officer > 60 | 26,639% | 73,361% |
| Amount | |
|---|---|
| Cost | 1649,96€ |
As can be seen from results for group of people over 60 years there are resources which were not fully utilized and on the other hand the amount of people between 15 and 59 remaining in simulation is too high to be a right model to be implemented.
Model 2
For the second model the only variable that is changed is duration which will be set to 8 hours (8:00 - 16:00) instead of 4 hours from Model 1. In this model citizens will also be given 30 minutes to leave the sampling point. Other variables remain unchanged.
| Group | Total generated | Remaining in system | Processed |
|---|---|---|---|
| Below 60 years | 1572 | 1139 | 433 |
| Over 60 years | 282 | 5 | 277 |
| Resource | Idle | Busy |
|---|---|---|
| Medical laboratory technician < 60 | 2,004% | 97,996% |
| Medical laboratory technician > 60 | 57,878% | 42,122% |
| Administrative worker < 60 | 1,655% | 98,345% |
| Administrative worker > 60 | 74,893% | 25,107% |
| Police officer < 60 | 4,167% | 95,833% |
| Police officer > 60 | 41,018% | 58,982% |
| Amount | |
|---|---|
| Cost | 2532,27€ |
In second model number of people between 15 and 59 is rising but really slowly and still there are people waiting to be tested for Covid-19. Also in this model significant rise in idleness of resources allocated for older people can be observed. The last important indicator, costs is rising as well which is not wanted from the state as the governments wants to achieve best price-performance ratio.
Model 3
Model 3 will be adujsted differently than the previous one. Two more sampling points will be added to the model for citizens younger than 60 years and duration will be set to 6 hours (8:00 - 14:00).
| Group | Total generated | Remaining in system | Processed |
|---|---|---|---|
| Below 60 years | 1755 | 1210 | 545 |
| Over 60 years | 322 | 9 | 313 |
| Resource | Idle | Busy |
|---|---|---|
| Medical laboratory technician < 60 | 2,112% | 97,888% |
| Medical laboratory technician > 60 | 37,607% | 62,393% |
| Administrative worker < 60 | 1,185% | 98,815% |
| Administrative worker > 60 | 59,638% | 40,362% |
| Police officer < 60 | 3,902% | 96,098% |
| Police officer > 60 | 35,505% | 64,495% |
| Amount | |
|---|---|
| Cost | 2856,53€ |
Model 3 with adjusted number of sampling points for people below 60 and adjusted time is still facing the same issue as the previous ones. High number of people below 60 waiting in the sampling point to have their Covid-19 tests done.
Model 4
Last model in this simulation will be adjusted more "drastically". Duration will be set back to 8 hours (12:00 - 16:00) in order to evenly distribute people coming to be tested and number of sampling points for citizens below 60 will be set to 8 and as a result of idleness of resources allocated for people over 60 the number of sampling points belonging to them will be set to 2.
| Group | Total generated | Remaining in system | Processed |
|---|---|---|---|
| Below 60 years | 1487 | 227 | 1260 |
| Over 60 years | 259 | 7 | 252 |
| Resource | Idle | Busy |
|---|---|---|
| Medical laboratory technician < 60 | 3,949% | 96,051% |
| Medical laboratory technician > 60 | 25,015% | 74,985% |
| Administrative worker < 60 | 17,396% | 82,604% |
| Administrative worker > 60 | 46,489% | 53,511% |
| Police officer < 60 | 67,056% | 32,944% |
| Police officer > 60 | 36,560% | 63,440% |
| Amount | |
|---|---|
| Cost | 3347,22€ |
Conclusion
From all 4 models described in this paper the last one seems to be the most optimal one to be implemented. Mainly, it is because during the simulation this model serves the highest number of citizens coming to be tested (both young and old ones). On the other hand cost increase can be observed but considering the fact that majority of people will be tested in one day such an increase in costs of just over 1,600€ in comparison to Model 1 is negligible.