Exponenciální rozdělení

Úvod

Exponenciální rozdělení představuje jedno ze základních pravděpodobnostních rozdělení. Společně s rovnoměrným, normálním či logritmicko-normálním rozdělením spadá do spojitých rozdělení. Náhodná veličina, která má exponenciální rozdělení, představuje dobu čekání mezi dvěma jevy, které nastávají s pravděpodobností mající Poissonovo rozdělení (např. doba mezi dvěma nehodami na dálnici). Dalo by se tedy říct, že exponenciální rozdělení je spojitým protějškem Poissonova rozdělení.
Jako příklad souvislosti Poissonova a exponenciálního rozdělení lze uvést již zmíněné autonehody na dálnici. Poissonovo rozdělení zde popisuje počet autonehod na dané dálnici za určitý časový interval, například v průměru 2 autonehody za den. Exponenciální rozdělení pak popisuje dobu do výskytu první autonehody, nebo dobu mezi dvěma autonehodami. V tomto příkladu by to bylo v průměru 1/2 dne (střední hodnota těchto dvou rozdělení je vzájemně převrácenou hodnotou).

Terminologie

Definice

Obr. 1: Funkce hustoty pravděpodobnosti exponenciálního rozdělení

Obr. 2: Distribuční funkce exponenciálního rozdělení

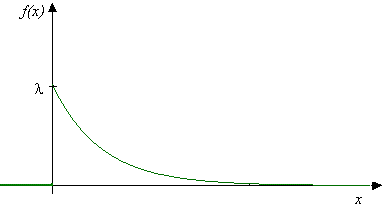
Spojitá náhodná veličina X má exponenciální rozdělení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Exp(\lambda)} , právě tehdy, když má funkce hustoty pravděpodobnosti tvar:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)=\begin{cases} \lambda e^{-\lambda x}, & \text{pro }x>0 \\ 0, & \text{pro }x\le 0 \end{cases}}

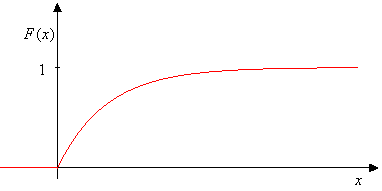
Distribuční funkce je potom popsaná rovnicemi:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)=\begin{cases} 1-e^{-\lambda x}, & \text{pro }x>0 \\ 0, & \text{pro }x\le 0 \end{cases}}

Vlastnosti

Jednoparametrové exponenciální rozdělení se značí jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X \sim Exp( \lambda )} , kde parametr Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} představuje střední hodnotu počtu jevů, které nastanou v daný časový interval. Jelikož počet jevů je vždy kladné číslo, tak pro parametr platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda>0} . Střední hodnota exponenciálního rozdělení se pak počítá jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX={1 \over \lambda}} a rozptyl exponenciálního rozdělení se počítá jako Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle varX={1 \over \lambda^2}} .

Vlastnosti exponenciálního rozdělení

Značení	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X \sim Exp( \lambda )}
Parametry	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda>0}
Nosič	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X \in (0,\infty)}
Hustota pravděpodobnosti	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)=\begin{cases} \lambda e^{-\lambda x}, & \text{pro }x>0 \\ 0, & \text{pro }x\le 0 \end{cases}}
Distribuční funkce	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)=\begin{cases} 1-e^{-\lambda x}, & \text{pro }x>0 \\ 0, & \text{pro }x\le 0 \end{cases}}
Střední hodnota	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX={1 \over \lambda}}
Rozptyl	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle varX={1 \over \lambda^2}}

Reálné aplikace

Jak již bylo zmíněno, exponenciální rozdělení popisuje dobu čekání na určitý jev, či dobu mezi dvěma jevy, jejichž výskyt je dán Poissonovým rozdělením. Obě tato rozdělení hrají důležitou roli například v teorii spolehlivosti či v teorii hromadné obsluhy.

Teorie spolehlivosti

Teorie spolehlivosti zahrnuje problematiku související s konstrukcí výrobků, s použitými materiály a s diagnostikou údržby a soustředí se na odhady a optimalizaci bezporuchového provozu výrobků. Spolehlivost výrobku lze popsat jako jeho vlastnost splňovat určitou funkci po danou dobu a za daných podmínek.
Teorie pravděpodobnosti a matematická statistika zde mají hlavní roli v určování odhadů a stanovování prognóz ohledně bezporuchovosti či životnosti výrobků. Pravděpodobnost poruch se v životě výrobku popisuje právě pomocí exponenciálního rozdělení. Porucha výrobku často nastává v libovolném čase, což znamená, že proměnná tohoto rozdělení (v tomto případě je proměnnou čas, x=t) je nezávislá. V rámci teorie spolehlivosti se kromě distribuční funkce F(x) a hustoty pravděpodobnosti f(x) také často počítá pravděpodobnost bezporuchového provozu (někdy také nazývána jako funkce spolehlivosti), která je dána vztahem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R(x)=1-F(x)=e^{-\lambda x}} , a veličina intenzita poruch, která je dána vztahem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda(x)=\frac{f(x)}{R(x)}=\frac{\lambda e^{-\lambda x}}{e^{-\lambda x}}=\lambda} .

Příklad

Na základě pozorování žárovek do světlometů bylo zjištěno, že za sledovaný čas se vyskytlo 80 poruch, přičemž akumulovaný pracovní čas žárovek byl Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_{ak}=22500 \text{ hod}} . Údaje z pozorování jsou zpracovány v tabulce níže. Jaká je střední doba do poruchy? Za jaký čas dosáhne pravděpodobnost poruchy 10 % (tj. jaký je 10% kvantil)?

Údaje z pozorování žárovek

Doba do poruchy (hod)	Absolutní četnost poruch	Akumulovaný pracovní čas Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_{ak}}
150	31	22500 hod
300	22
450	13
600	7
750	4
900	2
1050	1
	Celkem 80 poruch

Řešení: Nejprve vypočítáme střední dobu do poruchy žárovek, tj. jak dlouho v průměru trvá žárovce, než se rozbije:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Ts=\frac{T_{ak}}{n}=\frac{22500}{80}=281 \text{ hod}}

Nyní známe střední hodnotu rozdělení, a tudíž lze ze vztahu pro střední hodnotu rozdělení (EX) vypočítat intenzitu poruch Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} , která představuje převrácenou hodnotu střední hodnoty:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\lambda}\Rightarrow \lambda =\frac{1}{EX}=\frac{1}{281}=0,00356 \text{ poruch za hodinu}}

Pravděpodobnost poruchy pak popisuje distribuční funkce. V tomto příkladu ale známe pravděpodobnost poruchy (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p=0,1} ) a hledáme čas (proměnnou x), kdy bude této pravděpodobnosti dosaženo. Je tedy třeba si nejdřív z distribuční funkce vyjádřit x:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)=1-e^{-\lambda x}}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1-F(x)=e^{-\lambda x}}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \ln{(1-F(x))}=-\lambda x}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x=\frac{\ln{(1-F(x))}}{-\lambda}=\frac{\ln{(1-0,1)}}{-0,00356}=29,6 \cong 30 \text{ hod}}

Střední doba poruchy je tedy 281 hodin a pravděpodobnosti poruchy 10 % dosáhne žárovka přibližně po 30 hodinách.

Teorie hromadné obsluhy

Teorie hromadné obsluhy (někdy také nazývaná teorie front) představuje vědní disciplínu, která se zabývá systémy hromadné obsluhy. V takovém systému dochází k obsluhování a vyřizování příchozích požadavků, které se mohou hromadit a tvořit fronty. Požadavkem může být jakákoliv jednotka, která přichází do systému za účelem obsluhy (například pacient u lékaře, auto v servisu či tisková úloha v tiskárně).
K popisování systémů hromadné obsluhy se stejně jako u teorie spolehlivosti využívá matematická statistika a teorie pravděpodobnosti. Nejčastěji se zde využívá právě exponenciální a Poissonovo rozdělení.
Poissonovo rozdělení zde popisuje tzv. intenzitu příchodů (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} ) a intenzitu obsluhy (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} ). Intenzita příchodů představuje průměrný počet požadavků, které přijdou do systému hromadné obsluhy za určitou časovou jednotku (například do ordinace přichází v průměru 5 pacientů za hodinu). Intenzita obsluhy pak představuje průměrný počet obsloužených požadavků za určitou časovou jednotku (například doktor vyšetří v průměru 4 pacienty za hodinu).
Exponenciální rozdělení zde pak nejčastěji popisuje tzv. příchod požadavků do systému (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\lambda}} ) a obsluhu požadavků v systému (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\mu}} ). Pojem příchodu požadavků do systému představuje průměrnou dobu mezi příchody dvou po sobě jdoucích požadavků (například nový pacient přijde do ordinace v průměru jednou za 12 minut). Obsluha požadavků v systému pak vyjadřuje průměrnou dobu obsluhy jednoho požadavku (například doktor vyšetří jednoho pacienta v průměru za 15 minut).

Příklad

K bankomatu chodí v průměru 10 lidí za hodinu. Každý člověk stráví u bankomatu průměrně 2,5 minuty. Jaká je průměrná doba mezi příchody dvou zákazníků? Jaká je intenzita obsluhy? Jaká je pravděpodobnost, že do jedné minuty od odchodu posledního zákazníka přijde další?

Řešení: Ze zadání známe intenzitu příchodů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda=20} lidí za hodinu a průměrnou dobu obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\mu}=2,5 \text{ min}=0,041\bar{6}\text{ hod}} (nutné převést na společné časové jednotky). Z těchto hodnot lze snadno vypočítat průměrnou dobu příchodů a intenzitu obsluhy. Jedná se o převrácené hodnoty již známých hodnot.

Průměrná doba příchodů: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\lambda}=\frac{1}{20}=0,05 \text{ hodiny}=3 \text{ minuty}}

Intenzita obsluhy: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle EX=\frac{1}{\mu}\Rightarrow \mu=\frac{1}{EX}=\frac{1}{0,041\bar{6}}=24 \text{ lidí za hodinu}}

Nyní známe jak průměrnou dobu příchodů, tak intenzitu obsluhy. Stačí už jen vypočítat pravděpodobnost, že do 1 minuty (1/60 hodiny) od odchodu posledního zákazníka přijde další. V tomto případě nám poslouží distribuční funkce, kde proměnnou je v tomto případě čas (x=t):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)=1-e^{-\lambda x}}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F(x)=1-e^{-20\cdot \frac{1}{60}}=0,2835}

Pravděpodobnost, že do jedné minuty od odchodu posledního zákazníka přijde další, je 28,35 %.

Funkce v Excelu

Hodnoty hustoty pravděpodobnosti a distribuční funkce exponenciálního rozdělení lze v prostředí Excelu získat pomocí funkce EXPON.DIST(). Tato funkce má tři parametry:

• x — hodnota proměnné, neboli hodnota náhodné veličiny, pro kterou hledáme danou pravděpodobnost výskytu
• lambda — střední hodnota četnosti výskytu, neboli převrácená hodnota průměrné doby mezi jevy
• kumulativní — nabývá hodnot 0 či 1 a určuje, zda bude pro výpočet použita funkce hustota pravděpodobnosti (0, nekumulativní funkce) nebo distribuční funkce (1, kumulativní funkce)

Příklad

Internet ve firmě vypadne průměrně každých 10 hodin. Jaká je pravděpodobnost, že po posledním výpadku internet opět vypadne během následujících 6 hodin?

Řešení: V zadání je důležité slovo „během“, které nám napovídá, že se ptáme na kumulativní funkci, tedy na distribuční funkci (zajímá nás pravděpodobnost, že jev nastal v intervalu od 0 do 6 hodin od posledního výpadku). Hodnota proměnné je zde oněch 6 hodin, pro které zjišťujeme danou pravděpodobnost a hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} je zde převrácená hodnota průměrné doby mezi jevy, tj. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{1}{10}=0,1} .
Do Excelu vložíme tuto funkci:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle =EXPON.DIST(6;0,1;1)}

Výsledkem je, že pravděpodobnost, že po posledním výpadku internet opět vypadne během následujících 6 hodin, se rovná 45,12 %.

Příklady k procvičení

Zde můžete najít pár příkladů na procvičení. K některým výpočtům lze použít i výše zmíněnou funkci nástroje Excel. Řešení příkladů naleznete zde: řešení.

Příklad 1

Náhodná veličina má funkci hustoty pravděpodobnosti:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x)=\begin{cases} 0,1 e^{-0,1 x}, & \text{pro }x>0 \\ 0, & \text{pro }x\le 0 \end{cases}}

Jaká je střední hodnota a rozptyl této náhodné veličiny?

Příklad 2

Na trase mezi kolejemi VŠB v Ostravě-Porubě a magistrátem v centru Ostravy délky 10,5 km napočítali cestáři 86 děr v silnici.

1. Jaká je pravděpodobnost, že narazíme na díru v silnici při ujetí úseku délky 100 m na této trase?
2. Jakou vzdálenost je třeba na této trase ujet, aby pravděpodobnost, že narazíme na díru v silnici byla 99 %?

Příklad 3

Žárovky mají průměrnou životnost 2000 hodin. Předpokládáme, že doba, po kterou žárovka svítí, je náhodná veličina, která má exponenciální rozdělení.

1. Popište tuto náhodnou veličinu pomocí funkce hustoty pravděpodobnosti a distribuční funkce.
2. Jaká je pravděpodobnost, že žárovka vydrží v provozu nejvýše 1000 hodin?
3. Jaká je pravděpodobnost, že žárovka vydrží v provozu v rozmezí 1000 až 2500 hodin?