Monte Carlo method

Introduction and history

John von Neumann
Born: December 28, 1903 Budapest, Austria-Hungary Died: February 8, 1957 (aged 53) Walter Reed General Hospital Washington, D.C., United States Institutions: University of Berlin Princeton University Institute for Advanced Study Site Y, Los Alamos

Stanislaw Ulam
Born: April 13, 1909 Lemberg, Austria-Hungary (now Lviv, Ukraine) Died: May 13, 1984 (aged 75) Santa Fe, New Mexico Institutions: for Advanced Study Harvard University University of Wisconsin Los Alamos National Laboratory University of Colorado University of Florida

Monte Carlo method is a stochastic method using pseudorandom numbers. We can also say it is a class of algorithms for the simulation of systems. We can use it for solving mathematical problems as calculating integrals, particularly multidimensional where conventional methods are not effective. This method has wide range of application - from simulation experiments through computation of definite integrals up to for example solving differential equations. The basic idea of this method is very simple. We want to determine the mean value of the variable that is the result of random action. Let's imagine creation of a computer model of that action and after a sufficient amount of simulations, data may be processed by conventional statistical methods, for example to determine the average and standard deviation. Monte Carlo method was formulated and also used during World War II by scientists John von Neumann and Stanislaw Ulam in the United States in the development of atomic bomb. A research of neutron behavior and its feasibility of penetration various substances raised the problem of how to determine the percentage of neutrons in a spray that penetrates for example the water tank of certain dimensions. It wasn't possible to find a practical method to predict further behavior of individual neutron, to predict the entire further "history of his life." Neumann and Ulam used for modeling the prediction of "history of neutron life " Monte Carlo method inspired in roulette wheel technique (from here was the idea for the name Monte Carlo). Using this method it is possible to predict the trajectory of each neutron of the given bundle. Simulation of neutron motion wandering in water and randomly colliding with atoms of hydrogen and oxygen was done as follows:

"Is known that random event - that neutron is absorbed by hitting the hydrogen atom - will occur in one of hundred possible cases on average. To map the route of neutron is spinned the roulette wheel divided into one hundred parts, and among them only one part is indicating the "neutron absorption by a hydrogen atom." If the roulette wheel stops on that part, it indicates the "end of life" of neutron. In opposite case is possible by the another roulette wheel to determine the direction and speed of the neutron after collision. Then with another roulette wheel is possible to determine the trajectory that neutron will take before the next collision occurs. Simulation of "history of life" of neutron is performed as long until the neutron is absorbed, or until it lose such energy that the final exit of the neutron is no longer interesting for us, or until the neutron manages to escape without damage from the tank. When we will make a large amount of such simulations, we get more or less accurate information about percentage of neutrons that have managed to escape from the tank. The accuracy of this method is determined by mathematical-statistical methods of estimation theory." František Fabian, Zdenek Kluiber, Metoda Monte Carlo a možnosti jejího uplatnění, Praha: Prospektrum, 1998, page.13-14

Despite fact this is a very simplified example the nature of the Monte Carlo method is described close enough. The simulation would be of course very time consuming, in case it is actually necessary always spin the roulette. However, the authors worked at a time when the development of information technology was already in full progress, therefore they could use for these simulations simple computers (compared to current ones) that simulation time significantly shortened. The basic principle of Monte Carlo method has been spoken in 1777. In this year the French natural scientist Georges de Buffon formulated his famous needle problem - known as Buffon's task. It determines the value of the number π by random throwing a needle on paper with painted equidistant parallels. Very simply, it is an experiment, when he throws a needle on sheet of paper. Paper is divided by parallel lines and the needle is the same size as the distance between the lines. The result is that the probability of the needle crosses one of the lines is 2 / π. From this can be deduced π value. In 1901 Lazzerini made 34 080 needle throws and got for number π value 3,1415929 which was really amazingly good result. This method was at first used in solving the physics problems, which were before then practically unsolvable. Gradually, with the development of computer technology and modeling theory, it began to be used in solving complex problems from such areas like technology, economy, activity of call centers, traffic management and in solving problems in mathematics itself. Monte Carlo method is useful especially wherever there is the solution of the problem in some way dependent on the probabilities.

Monte Carlo Method

With Monte Carlo method we solve probabilistic and deterministic tasks using many times repeated random iterations. The solution is based on the fact that we construct probabilistic task, which has identical solution with the original task. The obtained solution has a probabilistic nature. Monte Carlo method can be divided into two groups according to the procedure of the solution or let say there are two possible approaches to solving problems by Monte Carlo method - the "geometric method" and the "calculation based on the estimation of certain characteristics of the random variable".

Geometric method

The geometric approach we have already met in the Buffon's task. Now, on a simple example let me show what other way can experimentally determine the value of π. To solve we use random number generator software Microsoft Excel (RAND function).

Calculation of π value

Is given unit square, which is inscribed with circular sector (see picture n.1). Using geometric approach we experimentally determine the value of π.

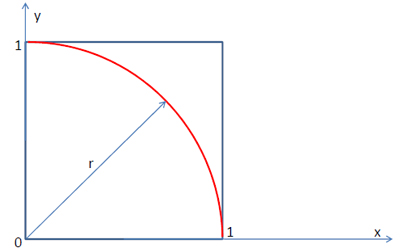
Picture n.1

Define event A - randomly selected point of the unit square is located in a circular sector. Based on the geometric probability, we can write the probability of the event A:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(A)=\dfrac{\dfrac{\pi*r^2}{4}}{r^2} }=\frac{\pi}{4}}

Now we need to perform a series of random experiments - choose a random point X from the square unit. Point X is determined by two independent uniformly distributed x and y coordinates, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0 \le x \le 1} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0 \le y \le 1} The concrete realization of x and y coordinates can be obtained in MS Excel using the RAND function which generates uniformly distributed random numbers from the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle <0, 1)} .

If a pair of x and y coordinates is generated, we can proceed to determine whether there was success (point lies in the circular sector) or failure. We can say that for the distance d of point X [x, y] from the origin of the coordinate system is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle d=\sqrt{x^2+y^2}}

Success therefore will occur if the i-th point can be decribibed as follows:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sqrt{x_{i}^2+y_{i}^2}\le1}

If there is m successful experiments out of n takes, where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle m \le n} , we can for the probability of event A write:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(A)\approx\frac{m}{n}} , so we get Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{m}{n}\approx\frac{\pi}{4}\Rightarrow\pi\approx4*\frac{m}{n}} .

Number of realized attempts	Number of succesful attempts	Determined estimate of π value
100	74	2,96000
1 000	782	2,96000
65 532	51 503	3,14369

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi \dot= 3,1415926539} It should be remembered, however, that in all cases there is a point estimate of the value of π.

Calculation based on the estimation of certain characteristics of the random variable

This approach can be used for example for the calculation of integrals.

Calculation of integrals

Let ξ be a continuous random variable defined on the interval (a, b) with the probability density f (x). We are interested in the continuous function η = g (ξ). Let a finite mean value of the function g (ξ) is defined by:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E[g(\xi)]=\int_{a}^{b}g(x)*f(x)dx}

If we make n realizations Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_{1}, ..., x_{n}} , we can take the value of the integral I as the arithmetic mean of the values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g (x_{i})} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I \approx \frac{1}{n} \sum_{i=1}^n g(x_{i})} . The task is to calculate the definite integral: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I=\int_{a}^{b}g(x)dx} . Let choose a continuous distribution defined on the interval (a,b) described by probability density f(x) so that it applies: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int_{a}^{b}f(x)dx=1} . Edit the given integral into: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int_{a}^{b}\frac{g(x)}{f(x)}*f(x)\, dx}

The integral we are able to determine. The procedure is as follows:

• Generate values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_{1}, ..., x_{n}} from distribution defined by density f(x)
• Calculate values of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g(x_{i})} , which brings realization of random variables with the same distribution
• When we take sufficiently large number of attempts n, the arithmetic mean of the values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g(x_{i})} can be considered as an estimation of the values of the integral: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle I \approx \frac{1}{n} \sum_{i=1}^n g(x_{i})}

Basic scheme of calculation by Monte Carlo method

General basic scheme of calculation by Monte Carlo method is as follows:

• Generate random numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{i}} with uniform distribution on the interval (0,1).
• Transform random numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y_{i}} into random numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_{i}} with the required distribution.
• Using random numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z_{i}} we can directly calculate estimates of the characteristics of random variable X, or we can calculate it using appropriate algorithms of values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_{i}} and estimates of characteristics of random variable.
• The results are statistically processed.

Calculation by Monte Carlo method is based on the modeling of random process and on the processing of results using statistical methods. To achieve the required accuracy is required multiple repeat simulations. Together with estimating unknown value is important to determine the accuracy of the estimation.

Accuracy of Monte Carlo method

An important part of Monte Carlo methods is to determine accuracy of our estimation. So our wanted unknown variable X has been estimated using the implementation of the random variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \bar{X}} , whichever there is approximate equality between them: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X \approx \bar{X}} . This approximate equality has precision ε with confidence α, if the inequality Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \left |X - \bar{X}\right | < \epsilon} applies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(\left |X - \bar{X}\right |<\epsilon)=\alpha} . If we put ε=0,01 α=0,95, then in 95 cases out of 100, the approximate value differ from actual by not more than 0.01. Assume further that our unknown value we estimate by the arithmetic mean Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \bar{X}=\frac{1}{N}(X_{1}+X_{2}+...+X_{N})} . Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X_{1}+X_{2}+...+X_{N}} are independent random variables, equally divided, while Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(X_{i})=X} and have the final dispersion Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho^2} . According to the Central Limit Theorem has random variable Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \bar{X}} asymptotically (for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N \to \infty)} normal distribution with mean value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(\bar{X}=X)} and dispersion Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D(\bar{X}=\frac{\rho^2}{N}} . So for large enough N the following applies:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P\left (\frac{\left |X - \bar{X}\right |}{\rho^2}\sqrt{N}<t_{\infty}\right)}

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t_{\infty}} is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1 - \alpha}{2}} critical value of the standard normal distribution. Comparing this relation with the previous one, we get the relation: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon=t_{\infty}sqrt{\frac{\rho^2}{N}}} , thence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N=\frac{\rho^2}{\epsilon^2}t_{\infty}^2} . From this relation we determine the number of attempts N needed to achieve the required accuracy ε at the significance level α. We can also observe from these relations that given α and σ error decreases inversely with respect to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle sqrt{N}} . If we are estimating area content A, random variable m has binomial distribution with parameters n and p, with mean value E(m) = np and dispersion D(m) = np(1-p). According Moivre - Laplace sentence has such random variable for large enough n normal distribution, random variable has asymptotic distribution. So for sufficiently large n the following applies:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P\left (\frac{\left |\frac{m}{n}-p\right |}{\sqrt{p(1-p)}}\sqrt{n}<t_{\infty}\right)=\alpha}

For size of error we get the following relationship: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon=t_{\infty}\sqrt{\frac{p(1-p)}{n}}} , thence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n=\frac{p(1-p)}{\epsilon^2}t_{\infty}^2} .

In practice, the value of p is unknown, so we determine number of required attempts n to achieve certain accuracy as follows: choose Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{0}} as the value of p = 0.01. We realize Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{0}} attempts and calculate approximate value of p. Substitute into the previous formula and calculate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{1}} . If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{1}} is greater than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n_{0}} , we'll make additional attempts and re-calculate the approximate value of p. If the previous estimate differs substantially from the new one, then specify the value of n again.

Monte Carlo method use

Monte Carlo method has a wide range of applications. Generally speaking, it can be used wherever there is a solution which can be found by using many times repeated random attempts. Since this is a stochastic method, it is necessary to know the probability distribution of observed variables. These problems can be found in all areas, not only in mathematics but also in finance and commerce, physics and physical chemistry, in computing and games etc.

Calculation of integrals

One-dimensional integrals can be easily computed using numerical methods but some multidimensional integrals are not that easy to calculate. In these cases it is useful to compute them with Monte Carlo method. As you already know, to estimate the unknown value we can proceed with two approaches - geometric method or we estimate certain characteristic of random variable. To calculate the definite integral we can use both methods (I used the second one earlier).

The calculation of multidimensional integrals

For calculation of multidimensional integrals, we can also use both methods. The method is similar to the calculation of one-dimensional integrals, only the two-dimensional space we replace with multidimensional space.

Option pricing

At the beginning we generate a random element from the normal distribution Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon\simN(0, 1)} . Calculate the value of the asset at term of maturity. If we have daily data and we estimate price of an option with term of maturity, we simulate asset prices after the days until we get the price. The whole procedure is repeated N times. We receive N payments, from which we calculate their mean value, which in the end is discounted to the beginning.

Sensitivity and uncertainty analyzes

Monte Carlo filtering in general deals with the definition of a certain area from which may originate input factors to attain the output reached specific value (for example, the largest and lowest value etc..). Provides answers to questions as: What factors or group of factors are most responsible that the output will be located in certain area? Which parameters cause the stability (instability) of a dynamic system? The main idea of Monte Carlo filtering is a division of outputs Y into good and bad, those that fall into the desired area, and those that did not fall.

Gambling games

Gambling games are based on chance. As with other games is described a system of rules and sequences of moves. Precisely the results of turns are completely random at gambling - random turns (in other games where the turns are affected by the player the turns are called personal moves). Monte Carlo is an example of processes, where the system of personal moves will simulate a system of random moves. It were gambling games what were the basis for the emergence and development of the theory of probability. Monte Carlo or random and pseudorandom numbers generators allow mechanizing gambling games because they allow you to set all the alternatives of equal probability.

Computer graphics

Especially Quasi Monte Carlo method is used for rendering 3D models. Graphics programs have a feature that creates light reflections from various surfaces, Monte Carlo is generating them randomly within a hemispherical distribution, Quasi Monte Carlo produces them regularly. Usage - computer games, graphics, animation, special effects, architecture, etc. One of rendering methods is radiosity, based on the law of conservation of energy.

Conclusion

Monte Carlo method can be used to compute various numerical tasks - calculate integrals, either one-dimensional or multidimensional, value of the number π, or we can use this method to solve a system of linear equations. Using this method, is important firstly to model a random variable by which we estimated given task, and then prepare a given algorithm in some programming language. This method is also applicable in other areas such as economics or physics. In economics, for example, the development of share prices, or option pricing.