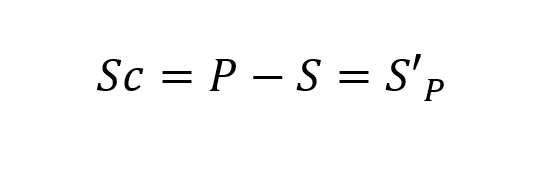Multiplayer cooperative games
Contents
Introduction
In previous chapters of Multiplayer games we have introduced already the topic regarding multiplayer games. In other words many player games or n-player games are part of Game theory, which focuses on games where are more than two players. It is considered as games with n ≥ 2 players, and every player has d ≥ 2 strategies to choose.
In real world the people will confront much more often with multiplayer games, than with pure 2 player games. In some way, the whole life and surviving on this planet could be stated as a multiplayer game, because every living person has to choose the way to act (strategy) and therefore affect the others.
In this chapter we will take a look at the multiplayer cooperative games.
Cooperative games
Cooperative game theory deals with situations where objectives of participants of the game are partially cooperative and partially conflicting. It is in the interest of participants to cooperate in the sense of making binding agreements to achieve the maximum possible benefit. When it comes to distribution of benefit/payoffs, participants have conflicting interests. Such situations are usually modelled as cooperative games.
In game theory, a cooperative game (or coalitional game) is a game with competition between groups of players ("coalitions") due to the possibility of external execution of cooperative behavior. Those are opposite to non-cooperative games in which there is either no option to forge coalitions or all arrangements need to be self-enforcing.[1]
Cooperative game theory provides a complex method as it only defines the structure, strategies and payoffs of coalitions, whereas non-cooperative game theory also looks at how bargaining events will affect the distribution of payoffs inside each coalition. As non-cooperative game theory is more general, cooperative games can be investigated over the approach of non-cooperative game theory provided that necessary assumptions are made to include all the possible strategies available to players due to the possibility of outdoor application of cooperation. While it would accordingly be optimal to have all games expressed below a non-cooperative outline, in many instances insufficient data is available to precisely model the formal procedures available to the players during the planned bargaining process, or the resulting model would be of too high complexity to offer a practical tool in the real world. In such cases, cooperative game theory provides a simplified approach that allows to investigate the game at large without having to make any hypothesis about bargaining powers.[1] [2]
When creating a mathematical model of the conflict, a distinction is made between a coalition of action and a coalition of interests. Coalition of action mentions to certain groups participating in the game and making decisions. Coalition of interests are collectives that participate in the game and protect some general interests. In addition, the concept of a situation is presented - the result of all coalitions choosing their strategies.
The game is called cooperative, or coalition, if players can join in groups, taking on some duties to other players and coordinating their actions. This is different from non-cooperative games in which everyone is forced to play for themselves. Recreational games are rarely cooperative, but such mechanisms are not unusual in normal life.
It is often expected that cooperative games differ exactly in the ability of players to communicate with each other. In general, this is not true. There are games where communication is allowed, but the players pursue personal goals.
Of the two types of games, non-cooperative games define situations in great detail and generate more precise results. Cooperatives reflect the process of the game as a whole. Efforts to combine the two approaches have yielded considerable results. The so-called Nash program has already found solutions to some cooperative games as equilibrium situations of noncooperative games.
Hybrid games include elements of co-op and non-co-op games. For example, players can form groups, but the game will be played in a non-cooperative style. This means that each player will follow the interests of his group, while at the same time trying to achieve individual profit.
Cooperative games are obtained in cases when, in a game of n players, it is allowed to form certain coalitions.
Cooperative Games with Transferable Utility
Games with Transferable Utility are games where the utility can be transferred by one player or coalitions to another, without incurring any losses, then it is called Transferable Utility (TU).[3]
For example:
n farmers can cooperate to grow fruit
- Each group of farmers can grow apples or oranges
- a group of size k can grow Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2k^2} tons of apples and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k^3} tons of oranges
- Fruit can be sold in the market: – if there are x tons of apples and y tons of oranges on the market, the market prices for apples and oranges are max{X - x, 0} and max{Y - y, 0}, respectively
- X, Y are some large enough constants
- The profit of each group depends on the quantity and type of fruit it grows, and the market price
Superadditivity and Cohesiveness
Superadditivity
Definition: a game G = (N, v) is called superadditive if v(C U D) ≥ v(C) + v(D) for any two disjoint coalitions C and D [3]
- Example: v(C) = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |C|^2} : – Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(C U D)} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (|C|+|D|)^2} ≥ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |C|^2} +Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle |D|^2} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(C) + v(D)} [4]
- In superadditive games, two coalitions can always merge without losing money; hence, we can assume that players form the grand coalition
In superadditive games, two coalitions can always merge without losing money; hence, we can assume that players form the grand coalition
- Convention: in superadditive games, we identify outcomes with payoff vectors for the grand coalition
i.e., an outcome is a vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x = (x1, ..., xn)} with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x(N) = v(N)}
Clearly, a superadditive game is cohesive. Cooperative (or coalitional) games simply define what each group of individuals can jointly achieve.
Cohesiveness
Cohesiveness is a special case of the stronger assumption, superadditivity, which requires Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S} ∪ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T) } ≥ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(S) + v(T)} for all disjoint coalitions S and T. [4]
Cohesiveness guarantees that the equilibrium coalition is the one that should form. The worth of other coalitions will influence how Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(N)} will be divided among the players. [4]
The Core
In game theory, the core is the set of possible allocations that cannot be enhanced upon by a subset (a coalition) of the economy's agents. A coalition is said to advance upon or block a possible allocation if the members of that coalition are better off under another feasible allocation that is equal to the first excluding that every member of the coalition has a different consumption bundle that is part of an aggregate consumption bundle that can be built from publicly available technology and the initial endowments of each consumer in the coalition.
An allocation is said to have the core stuff if there is no coalition that can improve upon it. The core is the set of all possible allocations with the core property.
The core of the game (N, V ) is the set of payoff vectors:
![]()
In other words, it is the set of possible payoff vectors for the grand coalition that no coalition can break. If such coalition S exists, we shall say that S can improve upon or block x, and x is deemed unstable. That is, in a context where any coalition can get together, when S has a blocking move, coalition S will create and walk back the grand coalition and its payoffs ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Xs} to get to a better payoff for each of the members of the coalition, a plan that is enforceable for them.
Shapley value
The Shapley value is a solution concept in cooperative game theory, which was introduced it in 1951. To each cooperative game it gives a exclusive distribution of a total surplus produced by the coalition of all players. The Shapley value is characterized by a collection of necessary properties.[5]
The Shapley value always occurs and it is unique. It can be driven as the only solution that meets the axioms of symmetry, additivity, and a dummy player axiom that says a player that does not add anything to any coalition obtains what he can achieve for himself.
The number of player which is given a coalitional game, according to the Shapley value, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (v,N)} is given by the formula :[5]
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \varphi_i(v)=\sum_{S \subseteq N \setminus \{i\}} \frac{|S|!\; (n-|S|-1)!}{n!}(v(S\cup\{i\})-v(S))} [5]
- n- is total number of the players
- the sum extends over all subsets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S} of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} not containing player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i}
Multiplayer cooperative games
In multiplayer cooperative games, where number of players more than 2, there is a situation where players should interact and cooperate with each other. But the question remains, with whom to cooperate and against whom. The group of players who choose strategies together is called the coalition from which the coalition games originate.
Multiplayer cooperative game theory deals with situations where objectives of participants of the game are partially cooperative and partially conflicting. It is in the interest of participants to cooperate in the sense of making binding agreements to achieve the maximum possible benefit. When it comes to distribution of benefit/payoffs, participants have conflicting interests. Such situations are usually modelled as cooperative games. While the book mainly discusses transferable utility games, there is also a brief analysis of non-transferable utility games.
Coalitions
A coalition is a group of players cooperating in the choice of strategies, or in the redistribution of winnings.
In fact, coalition games involve a set of players, designated N = {1, ..., N}, who strive to form cooperative groups, i.e. coalitions to strengthen their position in the game. Any coalition S ⊆ N is an agreement between the players in S acting as a unit. Coalition or alliance formation is ubiquitous in many applications.
Let P be a set of players and in a system of N players N is also called a grand coalition. The coalition is marked with capital letters of the alphabet: S, T, U, etc. The formed coalition S ⊆ P and the counter-coalition SC:
- The coalition can be one-member (different from political science).
- A grand coalition is a coalition of all players (different from political science).
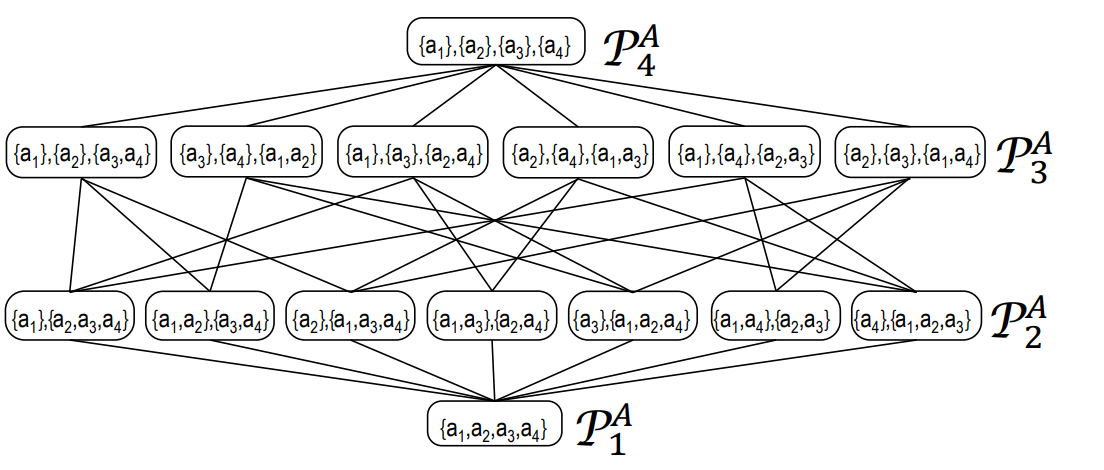
- Coalition structure is the set of all formed coalitions. For example here the coalition structure for 6 players ({1,4}, {2,3}, {5},{6}).
- Players {5}, {6} are one-member coalition, it means that these players do not cooperate with anyone. For typical conflict situations, a prerequisite is a game with a free disjunctive coalition structure. This coalition structure indicates that any coalition is allowed and a player can only be a member of one coalition.
Here is the graph example for 4 agents coalition.
Characteristic function
A characteristic function game is a pair (N, v), where:
- N = {1, ..., n} is the set of players and
- v : 2N → R is the characteristic function.
- for each subset of players C ⊆ N, v(C) is the amount that the members of C can earn by working together
Usually it is assumed that v is
- normalized: v(∅) = 0,
- non-negative: v(C) ≥ 0, for any C ⊆ N, and
- monotone: v(C) ≤ v(D), for any C, D such that C ⊆ D
- A coalition is any subset of N. N itself is called the grand coalition.
Voting
A voting game is a specific game that has only a score of 1 (accepted) or 0 (not accepted).
- The voting rule is a number specifying the minimum number of votes for the result 1 (accepted).
- A majority coalition is a coalition of players with more votes than indicated voting rule.
- A minority coalition is a coalition that does not have this number of votes. It is often a theoretical coalition that complements the majority coalition.
References
- ↑ 1.0 1.1 Wikipedia Cooperative game theory.[online].Available at:https://en.wikipedia.org/wiki/Cooperative_game_theory
- ↑ Non-Cooperative Game - Game Theory Available at: https://www.gametheory.net/dictionary/Non-CooperativeGame.html
- ↑ 3.0 3.1 3.2 Cooperative Game Theory [online]. Czech Technical University In Prague. Dostupné z: https://cw.fel.cvut.cz/b181/_media/courses/be4m36mas/mas2017-cooperative_games.pdf
- ↑ 4.0 4.1 4.2 Cooperative Game Theory [online]. Vrije Universiteit Amsterdam. Dostupné z: https://www.cs.vu.nl/~eliens/download/paper-cooperative-game-theory.pdf
- ↑ 5.0 5.1 5.2 Shapley value [online]. Wikipedia. Dostupné z: https://en.wikipedia.org/wiki/Shapley_value