N-Player prisoners dilema

Introduction

Let’s imagine a market with 5 companies. All of them are making the same product and each of them have around 20% of all customers. One day, a marketing company comes into the town and it offers its service to these 5 companies. Now the companies have a choice. Either to get an advertisement and get bigger part of the market, or to not advertise and save the money. But if all of the companies will advertise, they will again have 20% of market and they’ll lose money for advertisement. Now, this example seems quite easy. They can all make a deal not to advertise, and save the money. But what if one of them will betray the others and get an advertisement. Than the others will probably also advertise and all of them will be worse off. The trust will be lost and so the money.

Problem explanation

The N-player prisoners dilemma is a multiplayer (3 or more players) game in which the agents (players) have two different options. Either they can cooperate or they can defect. They are always better of when they defect, but when all cooperate, the group will have the best result. Let's take a closer look at the 5 companies. The total profit of all the companies is 1000 crowns. So each of them is making 200,- before the advertising company (ADCOM) comes. Remember, the advertisement won't make the total market bigger, it will just attract more customers to the advertised company. The ADCOM is charging 40,- for the advertisement and it says, that the first advertised company will get 50% more customers. So if one of the companies will buy this service, it will make total profit of 260,- (200 * 150% - 40) and the others just 175,-((1000 - 300)/4). But in total, the companies made 960,-. If all of them will buy the advertisement, all of them will make 160 crowns, total profit of all companies will be just 800,-. Let's see a table for better understanding.

Number of advertised companies	Profit of adv.com.	Profit of not adv.com.	Total profit
0	--	200	1000
1	260	175	960
2	235	150	920
3	210	125	880
4	185	100	840
5	160	--	800

As we can see, the advertise (defect) option is always better for the individual company, but the more companies defect, the more money is lost from the market. Unfortunately, this is just the beginning. Here are some questions that we can ask about this situation:

• Are the choices and actions of the agents simultaneous or distributed in time?
• Can individual agents see and adapt to the actions of others?
• Can they form coalitions?
• What are the agents’ goals in the game: to maximize their payoffs, to win a competition, to do better than their neighbors, to behave like the majority, or any other goal?
• Is it a one-shot game or an iterated one? If it is an iterated game, how will the next action be determined?
• What are the personalities of the agents? (Surely, different people react quite differently to the same conditions.) Can they change their personalities?
• Can an agent refuse participation in the game?
• Are the payoff curves the same for all agents?
• What are the payoff curves?
• How is the total payoff to all agents related to the number of cooperators?
• How are the agents distributed in space?
  • This is important for situations, where the communication and information flow is restricted by the factor of space. Players can for example communicate only with neighbors etc.

Let’s take a closer look to some of those questions:

Time distribution

Obviously, there is a big difference when all the players are making the choice in the same time or not. If all of the players have to do the decision in the same time, they cannot take decisions of others into account. Mostly, the players make the decision in different times. In that case, it’s important

• if there is a given order who’s turn is next or not
• if the player knows his position in the given order
• if the player knows the previous decisions of others

Communication/Visibility

There are several possibilities, how and if the players can communicate or see each other’s previous decisions. If there is no visibility, the players have to guess the moves of others. Of course, if they know the payoff curves, they can even count the previous moves out of their profit. Other possibility is for example to see neighbors only, random agents, fixed positions or everybody. This visibility, knowledge of previous moves, is crucial for some types of strategies and for creating and respecting the agreements or coalitions.

Coalitions

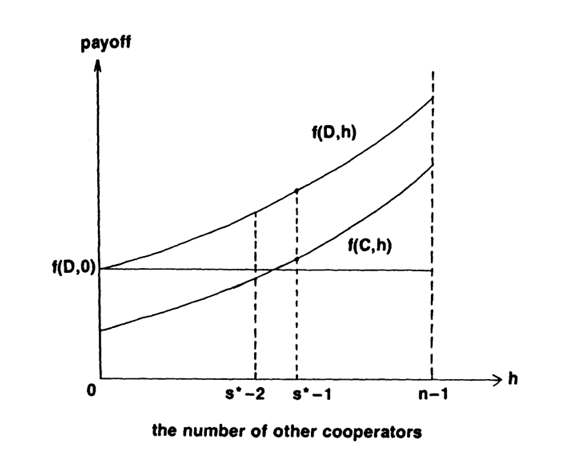
To show some how the coalitions can work, let’s make few assumptions.Let N = {1,2,3,.....,n} be our set of players. Each of them has an option to defect (D) or cooperate (C). Also let h to be number of other cooperators. (number of cooperators not including the decision-making player) Assumptions:

• The payoff difference f(D, h) - f(C, h) is positive and constant for all values h = 0, 1, ..., n-1. This payoff difference is denoted by α.
• f(C, h) is monotonically increasing in h = 0, 1, ..., n-1.
• f(C, n - 1) > f(D, 0).
• Payoff functions are well known to all players

If this all is true, than there exists a unique integer s*, 2 ≤ s* ≤ n, such that

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle f(C,s^*-2) < f(D,0) \le f(C,s^*-1)}

That means, s*-1 is the minimum number of other cooperators which will secure that if the player will cooperate, he will get better profit than when all of them will defect.

This number is really important when we are thinking about situation, where players can form coalitions. Let’s return to our example. Imagine that one of the companies (Alpha) is making decision about the advertisement. The situation is following: One company did buy the advertisement and it is making 260 crowns. The others including Alpha are making 175. The companies, that have no advertisement, formed coalition and they want not to advertise. They asked Alpha to join them.

Number of advertised companies	Profit of adv.com.	Profit of not adv.com.	Total profit
0	--	200	1000
1	260	175	960
2	235	150	920
3	210	125	880
4	185	100	840
5	160	--	800

If Alpha will join, it will make 175,-. But if it will advertise, it could make 235,-. That is better, but let’s see what will happen next. The coalition will make 150 each. That is less than when all of them would advertise. That means the coalition will most likely break. And then Aplha will be making also 160,-. That means it is maybe better to cooperate now, and make more, than when all of the companies would advertise. This is of course situation assuming that all companies know each other’s payoff curves, they can communicate and form coalitions, they know about decision of others and their goal is profit.

Tit for tat strategy

Iteration

Iterated games are much more complex than single-shot games. Players will react to the previous decisions and to the changing situation. There is also a difference, if the game has given end and if the players know how much rounds are left.

There was a tournament of different strategies in iterated n-person prisoner’s dilemma organized by Robert Axelrod. The players had to choose a strategy and then stick to it. The tournament was done by an algorithm in which the different strategies were entered. The winning strategy was “tit for tat”. It was very simple, cooperate in the first turn and then do whatever the opponents will. This was done for the 2 player version, but we can use this strategy even in N-player game. The difference will be, that the player has to have a “tolerance level”, that is the minimal number of defectors, which will trigger the defect reaction.

Personalities

The personality of the player is of course influencing his decisions. Economics is mostly presuming that people are behaving rationally. Which they in fact lot of times aren’t. But irrational behave is almost unpredictable, so the only way is to presume rationality. Other situation occurs when we know the players or if we can observe their previous games/moves and predict their next move based on that. But sometimes, the personality can change even in the game, for example when a company changes owner.

Real Applications

In real world we can meet a lot of examples of this game. But of course not all of them are studied or simulated. The simplest way to solve this dilemma is in fact to restrict the defect option by law or an agreement. This is used in many cases for example in agriculture, market and so on.

Market

First real world example can be our advertising companies model. But there are much more examples of this game in the market. Those are off course items for economics studies.

Example of N-player prisoner's dilemma

Environment

There are plenty of environmental examples. For the macro view, we can mention the global clime changes. For the micro view it can be pollution of local water sources by factories or even by local citizens. Those games are specific in the way, that cooperation has negative outcomes in the short term view. Imagine 5 companies again producing the same product and polluting one lake in one town. They know that if they won’t stop polluting the water, the town will lose all citizens and they will go bankrupt. But the clearing of their waste costs money and raises prices of their product. Hence the company that will clear its waste will probably go bankrupt even faster. So there is a high chance, that all of them will pollute.

Fortunately, situations like this are solved by long term agreements or restrictions. Agreements are based on the long term view. When even one of the companies won’t cooperate, the citizens will move and they all will go bankrupt, so the only rational choice is to cooperate. The restrictions are designed to change the payoff curves in such way, that defect option is way worse, than cooperating.

Nature

The next example we can find between animals. There are lots of species that are living in groups and also lots of others, living separately. The dilemma is to cooperate, be a part of a pack and share your food, space and so on, or to be on your own, more vulnerable, with risk of not finding any food at all.

References

See also

Prisoner's dilemma (czech version) http://www.simulace.info/index.php/Prisoner%27s_dilemma/cs