Predicting number of applicants for high school exams and their level of success in 2021
Contents
Problem Definition
This model serves to predict the population, number of applicants and number of the various kinds of tests that are written in the Czech generalised national high school entry exam, which is mandatory for all high school that end with the final "Maturita exam". As any prediction model drastically loses accuracy for the further years, it is designed in the way that it can be easily released for year 2022 when the real data for 2021 is available.
Method
The method for this work is Monte Carlo application in Excel, VBA is used as a more controlled substitute to Data Tables. The model uses the .xlsb format for the better optimazation of file size and efficiency.
Model
The model consists of 2 parts, one of them uses data from Czech Statistical Office(CZSO) and annual reports from Cermat to estimate the population, number of applicants and how many applicants will write which tests. The second part applies data from the first part on the distributions that we got from raw data from Cermat.
Demographics
The first part starts with 3 input tables from Cermat, the first one is the total number of applicants which we got from the the annual reports. It is expected that in the years where there were 2 rounds (2017-2019), only students that took part in the first round can take part in the second. This would match the absolute growth between 2019 and 2020 that was reported in Cermat’s latest press release as well. It’s worth noting that the data for 8 year High Schools is significantly higher in 2019 than in other years. The other two tables sum all tests taken that are present in the raw data.
The next table consists of CZSO’s yearly reports – population by age tables. Important things to notice in the table are the study type that is assigned to age on left (for the 4 year, 6 year and 8 year high school) and the fact that each generation gains number of people each year.
Because of that we are looking up the growths in the next table. We can generalize that the rate of growth is usually the same or higher. Therefore the rate of growth is set as normal distribution with the expected value same as the last growth traced, with standard error based on the data we have and probability limited to the top 50% of cases. As that means we cannot generate the value with the RAND() function, we’re replacing it with a more complex RANDOM() function. The last column in this table adds the estimated growth to the generations.
Population and applicants in history tables shows historical population for each type of study, number of applicants is added again for clarity. This serves as a base for calculation of shares between population and applicants throughout the years.
The next table calculates these shares with simple division, the data for 2021 is then predicted with normal distribution. The shares between applicants and tests looks at the shares of them, while 2021 prediction uses the same logic, the expected value for the normal distribution is much higher. As such the values can exceed realms of possibility, which has been counteracted by capping the shares to 99.5% The final table shows the forecasted values that are used in the second part of the model. Population is calculated by simple addition, the rest is the product of the estimated share and population and applicants respectively.
Cermat data analysis
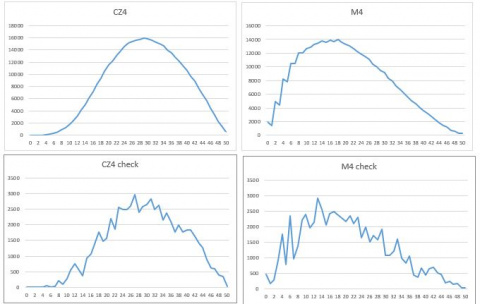
Raw data from Cermat includes all answers and points achieved for every question, it is also separated on sheets by each test term (1st Official term, 1st Substitute term, 2nd Official term, 2nd Substitute term – described as A,B,C,D respectively) The point gains have been summed and exported to the excel file. The data has then been transformed to consist of number of students that achieved each point count. For less bias Official terms have been combined with their Substitute terms, as the Substitute terms always have only a fraction of the students that took the Official ones. To find the distributions for points for each study type and subject, the data from all of the test through the years has been combined and plotted (Figure 1). From the data we estimate Normal distribution for Czech language and Log – Normal distribution for the Mathematics. Statistical analysis in a different software could estimate a more accurate distribution for the Mathematics.
To avoid the effect of numbers of applicant’s in the distribution the data has been changed to shares. The shares from the combined and plotted data has been used as the expected value, standard deviation of the preceding data is used as a standard deviation for the normal distribution. We are basically treating each possible point gain value as a different normal distribution, this allows us to avoid problems with unfitting assumed distributions. The sum of the new shares is obviously not 1 – which does not make sense for a probability distribution. The values are therefore corrected and adjusted, values less than 0 are turned to 0 and then they are divided by the adjustment factor, which is calculated as the sum of the unadjusted values.
Finally the number of students for each point gain value is calculated from the number of previously forecasted tests and the shares that we have generated in this point. These number are also plotted and compared with their matching source distributions for a sanity check (Figure 1). As the numbers have to be rounded, we end up with a new forecast for the number of tests taken. Since the difference in that is insignificant this is the number that will be used in the output. To prevent the issues with the size of the files, the output has been created in the separate file. The example output used for the results has 10000 iterations, however the model is made in a way that custom reports should be easy to generate.
Results
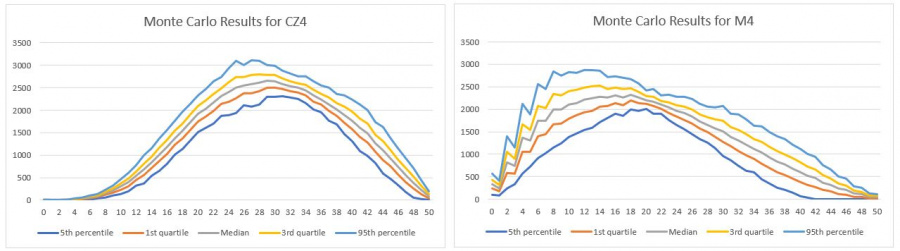
In Table 1 you can find the descriptive statistics of the outputted demographics data. 5th and 95th percentile are added so we can visually see the 90% confidence interval. To not repeat the obvious multiple times, I shall describe the meaning of the statistics only for Czech language tests for students of 4-year long high schools. There is a 90% likelihood that between 203253 and 203367 people will be in the age group that is able to apply for the high school. With the same likelihood 67057 and 72125 will actually apply for Cermat high school exams. There is 90% likelihood that the number of students that will write the Czech test will be anywhere between 64892 and 70123. All of the other data is read the same way.
These demographics were applied to the simulated distribution as can be seen in Figure 2. It is clear that the median distribution is of a nearly same shape as our baseline distribution of summed values, this is an expected behaviour. The detailed data for these graphs are included in the output files. The number are not viable to be shown in nongraphical way in this wikipage. It is derived from the raw outputted data with a simple Excel function.
Conclusion
The demographic part of this model can be used by Cermat to see how many applicants they can expect, the model in its entirety can be used either for high school to know how many students to prepare for and how will the point limit for their school will most likely look like or a students who would like to know how do they rank in country on average before the Cermat's annual report gets made many months later.
The best possible improvements for the model would lie in more accurate population estimates based on the detailed historical data of population, mortality and immigration. More advanced statistical methods could be used for the fitting the distribution which would require a more advanced statistical software (R,Python,Stata). Transformation of the model to a different program could also drastically improve the effiency and computation limits.
During the process of the model's creation it has become appearant that the model might not be immediatly useful as if the Covid-19 situation does not improve, Cermat tests will not be mandatory where they are mandatory now. That would turn the entire part of demographic data for applicants on its head, and would have a highly significant effect, that is impossible to quantify before the final decision is made by both the governement and the high schools themselves.
Source
- CZSO Annual Reports - 3 more for preceding years were used
- Cermat - Raw data
- Cermat main page - Basic information about present situation and the future