Queueing theory
The queueing theory is a mathematical method for analyzing the congestions and delays of waiting in line. The theory takes into consideration every component involved in waiting in line: process to serve, number of servers and number of customers. By reducing the theoretical results into Markov chains, it is possible to prove the correctness of its theorems. Usual task of the queueing theory is to predict the queue lengths and waiting times and optimize these results by changing its properties (i.e. type of the queue, number of servers-shop assistants). Its first thoughts were made by a Danish mathematician Agner Krarup Erlang at the beginning of the 20th century.
Contents
Motivation - why learn queueing theory?

Everyone hates waiting in queues, while everyone is forced to do it often. The queueing theory helps both parts of market - the customer has to wait shorter time, while the merchandiser has to pay less shop assistants. But the field of study doesn't focus only on the queues in the shopping malls.
Where is the queueing theory usually applied? These are the most common fields:
- Optimize the number of shop assistants in big shopping centers, so that the customers may wait shorter time, but the sellers may also use less shop assistants and therefore save money.
- Improve processes at banks or post offices - it is possible to simulate, what type of lines are the most appropriate under certain circumstances.
- Very often, it is used for improving manufacturing processes. Simulation of the production of items can result in more budget-wise systems, which can produce more goods in shorter time, thanks the the reduction of possible bottlenecks.
- Transportation systems simulations - by simulation of junctions, traffic lights can be configured, so that they help making the traffic as smooth as possible.
- Call centers - simulation can help predicting the number of incoming calls and the number of necessary operators.
Disclaimer: This chapter is written primarily for beginners and ones, who have only light background in operations research, computer science and industrial engineering. It is intended to be used as a study text, therefore you can find questions at the end of each part to make sure you understand the topic correctly. Important information are written in bold. Interesting - not necessary to remember - information can be found in box "Did you know...?"
Make sure you know enough...
- Name three different possible situations, where the queueing theory may help optimize the process.
- Let's say you're in a post office. What are the advantages of having only one line which belongs to multiple reception desks?
Classification
Classification tree: Mathematics > Applied mathematics > Operations research > Queueing theory
The queuing theory is considered as a branch of operations research, which belongs to the applied mathematics. Operations research is usually taught in faculties of engineering, public policy or business. This field focuses on the human-technology interaction and put an emphasizes on practical usage, searching for the best possible result (usually the maximum - profit, performance; or minimum - loss, risk, cost). Between other major operations research disciplines usually belongs: Computing and information technologies, financial engineering, manufacturing, service sciences, supply chain management, marketing engineering, policy modeling and public sector work, revenue management, simulation, stochastic models and transportation. [2]
| Questions in the end of each part should help you summarize what you know and challenge a little bit. Not sure how to answer one? Read suggested resources and look it up on Google. |
Make sure you know enough...
- Name at least two other subdisciplines of the Operations research and one subdiscipline of Applied mathematics.
- Which other mathematical disciplines may be useful to know for studying the queueing theory?
History
It all started in 1909 in a Copenhagen phone company, where an engineer Agner Erlang (1878-1929) asked himself: How many trunk lines are necessary to adequately service an entire city. [3] You could use just one, but that would result into huge delays, because the people would have to wait until the trunk is empty. Or you could install one for each phone, which would be extremely expensive and wasteful, since most people only call short time of the day. The telephone company needed a perfect compromise. Erlang found out, that knowing the average number of calls in an hour and the average call duration, one can estimate the number of trunk lines needed. The problem comes from the fact that the people can call in bunches, meaning that more people call at one time, and less later. Somebody can also block the trunk line longer than expected. Erlang came with a solution. He was able to count the number of trunk lines and get the percentage of callers with blocked calls, which made it possible to predict the adequate numbers for different time periods. And that was the beginning of queuing theory - when he published his work The Theory of Probabilities and Telephone Conversations.
Another important name connected with the theory, is David George Kendall (1918-2007), an English statistician, working mainly in field of probability. Kendall was the first to use the term Queuing theory, in his work "Some Problems in the Theory of Queues" (1951) [4]. He is well known for coming up with so-called Kendall's notation. It is a standard system used for describing and classifying a queuing node.
Even the Soviets contributed to the field of queueing theory more than little. Mathematicians Andrey Kolmogorov (1903-1987), Alexander Khinchin (1903-1987) were directly interested in this theory, often extending the theory of Andrey Markov (1856-1922) - Markov chains and Markov processes.
Make sure you know enough...
- Who is considered as the first to work on the queueing theory?
- What is a Kendall's notation?
Types of queueing systems
Queueing systems may have different structure. For example, there can be one line, multiple lines, one sever or more servers with complicated connection.
Queueing systems can be divided by these criteria[5]:
Source of customers
- Finite - the source of customers is finite, when it is possible and practical to count with the maximum possible number of customers.
- Infinite - usually, the source is considered as infinite, because the theoretical maximum value is too high.
Arrival of customers to the system
It can be described by two properties:
- Intensity of new customers - number of customers per one time unit.
- Interval between single tasks - time between two subsequent customers.
When we know one of these information, it is easy to figure out the second. The intensity and intervals may be divided in two possible types:
- Deterministic - the intervals between two subsequent customers (tasks) are fixed. This usually happens in manufactures.
- Stochastic - The arrivals vary, being described by some probabilities.
Service time distribution
The time spent while being serviced can be also either deterministic or stochastic. Most often, an exponential spread of a random variable X is being used.
Network of servers
The number of servers is crucial for the entire system. The goal of the queueing theory is to find the ideal number of servers, to satisfy both the customers and the owner.
- One server - this is the easiest type. Just one check desk in a small local shop for example.
- More servers parallel - the servers offer the same service. Typical example are the checking desks in big supermarkets. These can be further divided into another two categories: Having separate waiting line' for each server, or having one line for all, which then spreads.
Queue characteristics
This information shows, what rules are applied for letting the customer in the queue be served.
- FIFO - First In, First Out - the most common type. The one, who comes first, is also the first to be served. Classical queue in a shop.
- LIFO - Last In, First Out - servers always accept the ones, who are in the queue the shortest time.
- SIRO - Select in Random Order - the order, in which the customers joined the queue, is irrelevant, because the servers pick the customers randomly.
- PRI - Priorities - it is possible to set some priorities, which will help to decide, who goes first.
Special characteristics of queues
- Limit of queue capacity - shows the maximum capacity of the line, not allowing anyone else joining it, if reached.
- Patience of customers - it is possible (and also often very important), to take into account customer's patience. When the system doesn't care about it, it can be said, that the customers' patience is unlimited. It means, that they will wait in the queue as long as needed. But when the patience is limited, it is possible, that the customer simply rejects to join the line (and doesn't buy anything), because it is too long.
Make sure you know enough...
- What would happen, if LIFO type of queues were used in supermarkets?
- What are the advantages and disadvantages of single and multiple servers (cheking desks) in supermarkets?
- Name one process at place, where PRI type of queues is used.
Kendall's notation
Kendall's notation is a commonly used system for describing and classifying queues. Originally, these nodes were described by three factors A/S/c. Later, it has been extended to six factors - A/S/c/K/N/D:
- A = time between arrivals to the queue. Possible codes are: M (Markovian or memoryless - Poisson process), Mx (batch Markov), MAP (Markovian arrival process), BMAP (Batch Markovian arrival process), MMPP (Markov modulated poisson process), D (Degenerate distribution), Ek (Erlang distribution), G (General distribution), PH (Phase-type distribution).
- S = service time distribution. Possible codes: M (Markovian or memoryless), MY (bulk Markov), MMPP (Markov modulated poisson process), D (Degenerate distribution), Ek (Erlang distribution), G (General distribution), PH (Phase-type distribution).
- c = number of servers (service channels)
- K = capacity of the queue - the maximum capacity of customers in whole system (including the ones being served)
- D = queueing discipline - how to customers in the queue are being served
- N = size of population - the number of people who can possibly get into the system and become customers
Make sure you know enough...
- What does the M/m/1 queue in the Kendall's notation mean?
Suitable software
Java Modelling Tools
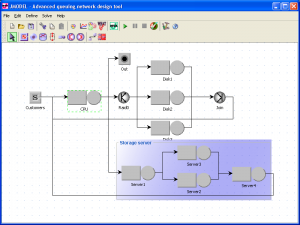
Java Modelling Tools (JMT) areapplications developed by Politecnico di Milano and Imperial College London, released under GPL license. At this time (January 2015), they include six applications:
- JSIMgraph - Queueing network models simulator with GUI
- JSIMwiz - Queueing network models simulator with wizard-based UI
- JMVA - Mean Value Analysis and Approximate solution algorithms for queueing models
- JABA - Asymptotic Analysis and bottlenecks identification of queueing network models
- JWAT - Workload characterization from log data
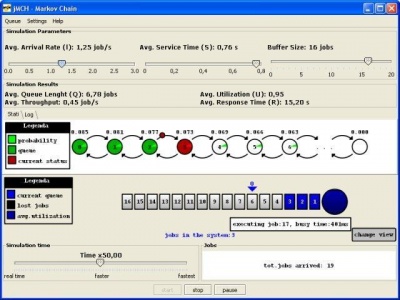
- JMCH - Markov chain simulator
Java Modelling Tools is platform-independent and requires only the Java Runtime Environment (version 1.6 or later). [6]
MATLAB
If you're interested in mathematics, solving difficult tasks and visualizing data, you probably know the MATLAB software. It can also be used for simulating the queues and application of it's theories.
Modelling
To make a mathematical model of the queue system, we need to use these variables:
- Entry of items
- Length of serving
- Network of servers
- Rules for leaving the queues to be served
- Specific parts of the system
| If you want to make simple calculations based on the queueing theory faster, you can use an automatic online tool. After opening the webpage, you have to choose the queueing model and input all required values. After the fast calculation is done, you get the results described in this chapter.
The tool can be accessed here: http://www.supositorio.com/rcalc/rcalclite.htm |
What sort of questions the mathematical model should answer about the line:
- How long does the service takes on average.
- How long do the people wait on average.
- What are the odds of the line being empty.
- How long is the line on average.
Make sure you know enough...
- How would you count, how long the service takes on average?
- Open the tool "Supositorio" and try it out.
Real world examples
These are two chosen examples from real world, where the application of the queueing theory had significant impact:
Prague public transportation
Queueing theory's results are used for setting traffic lights up. Engineers use several micro-simulation software programs, which can adequately simulate the movement of cars and people. It is possible to specify all necessary attributes like number of cars per time unit, size of the road, size of the cars, type of drivers (whether they are aggressive or not...). Traffic lights can also reply to current traffic situation, and for example let public transportation vehicles go faster, by allowing them to pass the junction quicker than the other roads. Using these optimizations saved 20 seconds in average for each bus and each optimised junction it is crossing, which can lead to millions of saved Czech crowns per year. [1]
Disney-world management of waiting lines
It wouldn't be very interesting to describe the process of optimizing and simulating of the waiting lines in Disney Parks, because it would be very similar to all such simulations. What they focus much more on is the psychological aspects of waiting. MIT professor Dick Larson says, that the main problem isn't the delay itself, but how it is experienced. “Disney has been the absolute master of this aspect of queue psychology,” says Larson. “You might wait 45 minutes for an 8-minute ride at Disney World. But they’ll make you feel like the ride has started while you’re still on line. They build excitement and provide all kinds of diversions in the queue channel.” It is possible thanks to series of chambers that the queue is passing, using LCD display's with interesting animations and other interactive tools.[7]
Make sure you know enough...
- Can you name three possibilities, how to make waiting in a queue more comfortable?
- Do you know some examples of comfortable waiting lines in your neighborhood?
External links
http://people.brunel.ac.uk/~mastjjb/jeb/or/queue.html
http://www.win.tue.nl/~iadan/queueing.pdf
http://wwwhome.math.utwente.nl/~boucherierj/onderwijs/Advanced%20Queueing%20Theory/AQTsheetshc1.pdf
http://www.mathworks.com/discovery/queuing-theory.html
https://mattachak.wordpress.com/2014/02/28/understanding-erlang-and-queuing-theory/
Resources
- ↑ 1.0 1.1 [ ČESKÁ TELEVIZE. Teorie front. 2007. Available at: http://www.ceskatelevize.cz/porady/10121359557-port/81-teorie-front/video/]
- ↑ [ What is Operations Research. Lancester University [online]. 2014 [cit. 2015-01-24]. Available at: http://www.lancaster.ac.uk/lums/study/masters/programmes/msc-operational-research-management-science/what-is-operational-research/ ]
- ↑ [ Agner Krarup Erlang. Plus Magazine - living mathematics [online]. 1997 [cit. 2015-01-24]. Available at: http://plus.maths.org/content/os/issue2/erlang/index]
- ↑ [ David George Kendall. St. Andrews University [online]. 1998 [cit. 2015-01-24]. Available at: http://www-history.mcs.st-andrews.ac.uk/Biographies/Kendall.html]
- ↑ [ ADAN, Ivo a Jacques RESING. Queueing Theory. Queueing Theory. 2002, n. 1. Available at:h ttp://www.win.tue.nl/~iadan/queueing.pdf ]
- ↑ [ Java Modelling Tools. JMT [online]. 2015 [cit. 2015-01-24]. Available at: http://jmt.sourceforge.net/ ]
- ↑ [ STEVENSON, Seth. What You Hate Most About Waiting in Line. Slate.com [online]. 2014 [cit. 2015-01-24]. Available at: http://www.slate.com/articles/business/operations/2012/06/queueing_theory_what_people_hate_most_about_waiting_in_line_.html]