Simple ecosystem simulation (NetLogo)
Contents
Simple ecosystem simulation
This problem is partly inspired by theory of "Primordial soup", partly by modern things such as agar.io game and partly by Swimbots simulation.
The primordial soup was a term created by Alexander Oparin in his theory of origin of the life on Earth. This theory states that there were just chemical elements which, under pressure and exposed to various energies (electrical discharges, high temperature), formed monomers, polymers and, in the end, live organisms. ( https://en.wikipedia.org/wiki/Primordial_soup )
Agar.io is a web-browser based game where the player controls his own cell. The cell can move, eject some of its matter and split itself in two. It can also absorb smaller cells which belong to other players. There is no particular goal in the game - just to, well, live long and prosper.
Swimbots is a simulation of the "gene pool" and originally was created as an answer to the statement of Richard Dawkins that:
"The very idea of a gene pool has no meaning if there is no sex. 'Gene Pool' is a persuasive metaphor because the genes of a sexual population are being continually mixed and diffused, as if in a liquid. Bring in the time dimension, and the pool becomes a river, flowing through geological time..." -Richard Dawkins, The Ancestor's Tale, page 432
Therefore swimbots are simulation where agents can move around in a "pool" and have two basic goals - 1) to eat and 2) to reproduce. Everything else emerges on its own during the simulation. Official web of the Swimbots is www.swimbots.com where the complete simulation app can be downloaded.
For purpose of our simulation we blended those three topics together and the result was a small artificial ecosystem which could have existed on the primeval Earth.
The blend is as follows:
Oparin's primordial soup already evolved into single-cell organisms - algae and protozoa. Some of protozoa are herbivorous (can eat single-cell algae), some of them "carnivorous" (can eat other protozoa). More detailed information is given in the problem statement but main idea of our work is to simulate what happens in the pool as the time goes on. We are insterested in this, because we want to determine if such a closed ecosystem could actually exist - and if it could, what is its equilibrium (here we consider the pool as an actual small puddle of water with all those happy little creatures in it, separated from the "outside" world).
Problem definition
Name of simulation: Simple ecosystem simulation
Class: 4IT495 Simulace systémů (LS 2015/2016)
Author: Petr Fišer
Type of model: Multi-agent simulation
Modelling software: NetLogo
We have three types of objects, algae (AL), herbivorous protozoa (HP) and carnivorous protozoa (CP).
Basic properties:
- Algae do not move, protozoa, on the other hand, do.
- They are not intelligent enough so they move randomly.
- Each protozoan has its movement speed (determined upon its creation) and a direction it is moving in.
- There is a 5% chance the direction changes.
- Algae emerge on their own.
- Frequency of algae regrowth is adjustable.
- HP can eat algae.
- CP can eat HP and CP. If CP eats AL, it does not count as consuming food (the AL disappears though).
- If protozoan consumes food (algae or other protozoa) it grows by a size of food it has just consumed.
- Protozoa can eat only smaller food than they are.
- "Eating" happens when two objects touch.
- Each object has a size.
- Size of the AL is always 1.
- Initial size (mass) of the HP is 3.
- Initial size (mass) of the CP is 5.
Life of a protozoa:
- When moving around, protozoa consume energy.
- The bigger they are, the more energy they need. Therefore, the mass of a protozoa continually decreases by 0,25% (HP) and 0,5% (CP), respectively
- Mass of protozoa decreases by at least by 0.001.
- When two objects collide (touch), "eating" happens.
- Two objects cannot overlay.
- When the cannot eat it, they stop moving in the given direction.
- If protozoan has mass equal to zero, it dies.
- If protozoan grows beyond two times of its initial size, it can reproduce by spliting itself.
- Beyond two times of initial size, the chance of splitting is 25%.
- Beyond three times of inital size, the chance is 50%.
- New protozoan does inherit speed atribute from its parent.
Starting conditions:
- A puddle of water with starting amount of AL, HP and CP scattered around. Those amounts need to be adjustable.
- Algae regrows (adjustable frequency).
Goal
Observe evolution of the ecosystem as a whole in order to determine if it is able to survive in the long run. If it is, then determine for which values of starting parameters there is an equilibrium formed in the ecosystem and determine ratios between count of algae,HP and CP respectively.
Used method and software
Multi-agent simulation using NetLogo.
Model
This section describes model implementation. First we show user interface and means for changing default inputs. Later, we will describe implementation on the level of functions called throughout the model. For complete programmer-level documentation, please, see the nlogo code itself.
User interface
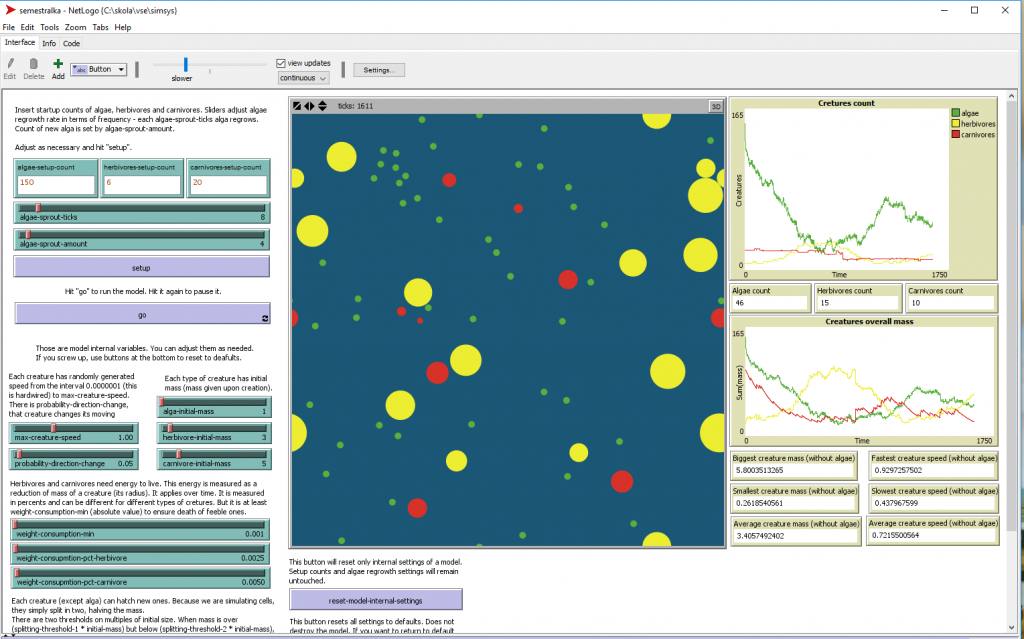
On the left side, we see simulation inputs and internal model variables. Variables which are meant to be set have their boxes above the "setup" button. Those are: initial number of algae, herbivores and carnivores and algae regrowth rate and amount. Model is run by hitting "go" button. Other inputs are internal model variables which are, generally, not meant to be fiddled with. They are there to make model more customizable for different purposes. During our simulation, those settings are left to default (because that is how the original problem was specified). Buttons not fully shown on the screenshot are used to reset internal model settings and to reset all settings to default, respectively.
On the right side, we see plots and counters. We observe counts of our creatures and also their overall mass. This is important because, as we see later, in some circumstances a supercreature can emerge - such a creature can fill the whole simulation window with its mass but in absolute counts, there is nothing else than this one creature. Other monitors give us a peek on the biggest/smallest and fastest/slowest creatures and also on the average values of speed and mass. In the center there is a simulation window. One important fact is that this is not only a place to show something, its size actually matters. As we see later, when simulation window (=puddle of water) is too small, the ecosystem is not able to survive for long.
Implementation
This section describes actual implementation of a simulation.
Agents (creatures)
There are three types of agents in the model - alga, herbivore and carnivore. Model consists only of agents. This is because we have to simulate collisions between them and modelling algae (algae do not move) as patches would cause troubles in computing collisions, not mentioning that a patch cannot have circular shape. Each agent - or "creature" as model internally calls it - has six attributes:
- creature-type - alga / herbivore / carnivore
- mass - mass of a creature, also used as a radius of circular body
- speed - a speed of a creature, as "distance per tick"
- already-existing - if it does exist or was freshly created (useful when creating new creatures)
- weight-consumption-pct - on every turn, creature consumes some percent of energy contained in its own weight
- initial-mass - initial (default) mass, 1 for AL, 3 for HP, 5 for CP
Most attributes are given to the creature upon its creation. This allows readjusting model parameters during the simulation without affecting already existing creatures. Type of creature determines its color, initial-mass and weight-consumption-pct. Shape is always circle and size attribute is set to twice the mass.
Mass of a creature continually decreases because a creature needs to consume energy in order to move (and live at all). This is governed by weight-consumption-pct (percent of current creature mass) but is always at least weight-consumption-min.
Each creature has a circular body. This is main difference from other NetLogo agent simulations where agent is treated more or less as a point. Agents (creatures) are created by three functions: breed-algae, breed-herbivores and breed-carnivores.
Each creature can split itsef when getting more than (splitting-threshold-1 * mass). There are two such thresholds because when creature has more than (splitting-threshold-2 * mass) it can have differrent splitting probability. Probabilities are given by splitting-probability-1 and splitting-probability-2, respectively, and are adjustable. Unlike other internal variables, splitting-* variables influence whole model including already existing creatures. Splitting is implemented by cell-split.
When created, each creature has direction it is facing. There is 5% (adjustable) probability that the direction changes. This is implemented by new-direction function.
Algae regrowth
Algae regrows during the simulation run. Its behavior is governed by algae-sprout-ticks (number of ticks between regrowth) and algae-sprout-amount (amount of alga in one regrowth). Regrowth is implemented by sprout-algae function. When sprouting, alga is placed in the simulation window in such a way that it is not overlapping any existing creature (including other alga). This is checked by collission detection routine.
Global parameters and variables
- max-creature-speed - max speed of a creature; generated as ((random-float max-creature-speed) + 0.000000000001)
- alga-initial-mass - initial mass of an alga
- herbivore-initial-mass - initial mass of a herbivore
- carnivore-initial-mass - initial mass of a carnivore
- probability-direction-change - probability that creature changes direction while moving
- weight-consumption-min - minimal (absolute) weight consumption
- weight-consupmtion-pct-herbivore - percentual weight consumption of herbivores
- weight-consupmtion-pct-carnivore - percentual weight consumption of carnivores
- algae-sprout-ticks - number of ticks, after which new algae will grow
- algae-sprout-amount - number of individual alga in one grow
- splitting-threshold-1 - creatures split when big enough, this is first threshold (multiple of mass)
- splitting-probability-1 - probability creature will split itself when bigger than threshold
- splitting-threshold-2 - the second splitting threshold
- splitting-probability-2 - splitting probability after second threshold can be different
- algae-setup-count - initial count of alga
- herbivores-setup-count - initial count of herbivores
- carnivores-setup-count - initial count of carnivores
- last-algae-sprouting - global counter how many go loops passed since last algae regrowth
Program functions
This is a printout of function headers with only a brief explanation of what they do. For more detailed information, please see the code.
- reset-all-settings - resets all settings to defaults
- reset-model-internal - settings - resets internal model settings to defaults
- setup - sets up the simulation according to given parameters
- go - main simulation loop
- check-collisions - checks collisions between agents
- process-collision [creature1-id creature2-id distance-delta] - if collission of agents is detected, this function is called to resolve it
- resolve-back-off [creature-who creature-who-away-from distance-delta] - when two creatures collide and none can eat the other, the smaller one has to correct its position
- process-eating [eater-id food-id] - when two creatures collide and one can eat the other, the bigger eats the smaller one
- process-nonweight-eating [eater-id food-id] - this function is called when carnivore collides with alga; carnivore eats it but does not gain weight
- place-nonconflicting [creature-id] - ensures agent placement such that it does not collide with those already placed, gives up after 500 (hardwired) tries to prevent inifinite loop
- cell-split - asks carnivores and herbivores to split themselves according to the splitting thresholds and probabilities
- consume-weight - asks carnivores and herbivores to lower their weight according to the weight-consumption-pct
- do-weight-decrease [decrease-pct] - this function realizes actual weight decrease of a creature
- sprout-algae - this method regrows algae
- breed-creatures [amount] - creates non-specialized creatures, is called from breed-algae, breed-herbivores and breed-carnivores
- breed-algae [amount] - creates algae
- breed-herbivores [amount] - creates herbivores
- breed-carnivores [amount] - creates carnivores
- (reporter) new-direction [previous-direction] - determines if creature should change its direction
- fuzz and hot-fuzz functions - those are not a part of the model but were used for fuzzing
Simulation setup
Before starting a simulation, we need to set it up. Because many functions are called internally from breed-* functions, the setup is very simple.
- clear-all
- set default creature shape as "circle"
- set patch color as "sky - 2"
- set last-algae-sprouting to zero
- create desired count of algae, herbivores and carnivores
- reset-ticks
Simulation go (main loop)
When simulation is set up, we can run it by calling go function in loop. go function looks as folows:
- try to sprout algae
- ask all creatures to move by forward speed command; alga has speed set to 0 so it does not move
- check for collisions and resolve them
- ask cells to split if they can and wish; the splitting algorithm ensures no new collissions are created during splitting
- decrease creatures' weight
- refresh creatures' directions
- tick
Movement and collision detection
Herbivores and carnivores move, algae, on the other hand, don't. Our problem statement is sort-of based on a fact that there is a limited space in a puddle and that creatures occupy significant space. They also cannot overlap (not even mentioning move one through the other). When two creatures touch, they can stop moving in that direction or eat each other. Each tick (each loop of go function), creatures move forward in the direction they are currently facing by a speed distance. The speed attribute of a creature can be understood as a "distance per tick".
Creatures have circular shape of size twice the creature's mass - mass is therefore a radius of a creature in the visualization window. For detecting collisions we had to create special routine. This routine, apart from working correctly, has to respect that if two creatures collide in a model, it would be good for them to collide optically. For this purpose, we stated mass as a radius of a creature.
Relying on the fact that creatures are circles, we can then check for collisions very simply: if (mass of agent1) + (mass of agent2) > (distance of agent1 to agent2), then there must have been a collision. Distance between agents is measured as a distance of centers of circle icons because that is how NetLogo draws them (size attribute of an icon is the same as diameter when icon is a circle).
We implement collision detection in check-collisions function which just takes every tuple of agents possible and checks for collision. If there was any, the process-collision is called on particular agents. The main decision block of process-collision looks as follows and decides possible combinations of colliding agents. Please note that we do not need complementary conditions like (creature1 alga and creature2 herbivore) and (creature1 herbivore and creature2 alga). This is because check-collisions generates all combinations of tuples (creatureX,creatureY).
...
if (creature1-type = "alga" and creature2-type = "herbivore") [
ifelse (creature1-mass >= creature2-mass) [
;; alga is bigger, herbivore backs off
resolve-back-off creature2-id creature1-id distance-delta
] [
;; alga is smaller, herbivore eats it
process-eating creature2-id creature1-id
]
]
if (creature1-type = "alga" and creature2-type = "carnivore") [
ifelse (creature1-mass >= creature2-mass) [
;; alga is bigger, carnivore backs off
resolve-back-off creature2-id creature1-id distance-delta
] [
;; alga is smaller, carnivore destroys it
process-nonweight-eating creature2-id creature1-id
]
]
if (creature1-type = "herbivore" and creature2-type = "herbivore") [
ifelse (creature1-mass >= creature2-mass) [
;; herbivore1 is bigger, herbivore2 backs off
resolve-back-off creature2-id creature1-id distance-delta
] [
;; herbivore2 is bigger, herbivore1 backs off
resolve-back-off creature1-id creature2-id distance-delta
]
]
if (creature1-type = "herbivore" and creature2-type = "carnivore") [
ifelse (creature1-mass >= creature2-mass) [
;; herbivore is bigger, carnivore backs off
resolve-back-off creature2-id creature1-id distance-delta
] [
;; herbivore is smaller, carnivore eats it
process-eating creature2-id creature1-id
]
]
if (creature1-type = "carnivore" and creature2-type = "carnivore") [
ifelse (creature1-mass = creature2-mass) [
;; both carnivores are of equal size, one of them backs off
resolve-back-off creature2-id creature1-id distance-delta
] [
if (creature1-mass < creature2-mass) [
;; carnivore1 is bigger, eats carnivore2
process-eating creature2-id creature1-id
]
]
]
Our collision system therefore works similarly to collision detection systems used in e.g. computer games - we forward the time by a small amount and then we check if collision happened. If it did, we react and either let one creature eat other or correct their positions in such a way that the are touching but not colliding.
Back off (position correction)
When two creatures collide and none can eat the other, one of them must correct the position so they are not colliding any more. We respect a "rule of the heavier" where the creature with higher mass stays on its position and the one with smaller mass moves in order to resolve the conflict. It is not necessarily moved backwards, it can bounce-off of the heavier creature. This is done by calculating how much creatures are overlapping and then setting heading property of smaller creature straight away from the heavier one. Direction is set to be parallel to line connecting centers of colliding creatures. Colliding creature is then moved by a distance of which they were overlapping.
Eating
When two creatures collide and one can eat another, eating happens. This is processed by process-nonweight-eating (when carnivore collides with smaller alga) and process-eating (for everything else) functions. Nonweight eating simply remove the eaten agent from the agentset. Regular eating transfers mass of creature that is being eaten to its devourer and repaints his icon.
Some new collision may occur after the creature enlarges, but in practice we observed them being with no significant effect on the simulation. With bigger creatures, the speed they move is small enough (compared to mass of a creature) that such collision will get resolved in next go loop anyway.
Splitting (making an offspring)
When creature gains enough mass, it can reproduce by splitting itself in two. The probability of splitting is governed by splitting-probability-{1,2} and the threshold after which it occurs is set by (splitting-threshold-{1,2} * initial-mass). Decision routine is this (algae do not reproduce):
;;mass over 2*initial-mass
if (((mass >= (splitting-threshold-1 * initial-mass))
and ;;but below 3*initial-mass
(mass < (splitting-threshold-2 * initial-mass))
and ;;generate random [0;1) and when lower than 0.25
((random-float 1) <= splitting-probability-1))
or ;;mass over 3*initial-mass
((mass >= (splitting-threshold-2 * initial-mass))
and ;;generate random [0;1) and when lower than 0.5
((random-float 1) <= splitting-probability-2)))
[
set size mass ;;make original creature half the size and move it
forward (mass / 2)
set mass (mass / 2)
hatch 1 [ ;;hatch a clone and move it in opposite direction
set heading (heading + 180)
forward (mass * 2)
]
]
Reproduction function is guaranteed to not create any new collisions. This is because it produces two creatures (the original and a hatched one) with half the mass who are positioned that they are touching (not colliding!) and heading in opposite directions. Their point of touch is where center of original creature used to be before it split. Using hatch, new creature inherits speed of the original one - as required by problem statement.
Results and observations
Main goal of the simulation was to determine if the ecosystem specified in problem statement can survive in a long run (with algae, herbivores and carnivores existing together). This was solved by fuzzing the input parameters and running the simulation numerous times. No matter the size of simulation plane - starting one was 128x128 patches, 5px per patch - the ecosystem shows following pathological states (PS):
- PS1 - Everything dies out on its own. This is caused mainly by clustering of alga in different region than most of herbivores are located (herbivores cannot gain mass). Both herbivores and carnivores cannot gain mass and die out.
- PS2 - Herbivores gain mass quicker than carnivores can eat them. This leads to state where all carnivores get smaller than initial-herbivore-size is and cannot eat them. Carnivores can eat only other very small creatures which turns out to be not enough. Gradually, herbivores outnumber carnivores who die out. System gets into equilibrium with only algae and herbivores and degenerates into predator-prey model. This model can run indefinitely.
- PS3 - Due to unlucky random positioning, herbivores gain mass quicker than carnivores can eat them. Carnivores get gradually smaller, but one still-surviving carnivore (and one is enough!) manages to eat few herbivores. The carnivore gets bigger almost explosively, consuming everything, sometimes forming supercreature (only one huge creature in the ecosystem). Then it splits itself into smaller carnivores who die out because there are no herbivores to eat.
- PS4 - The same scenario as PS3 initiated by frequent algae regrowth which enables herbivores to quickly gain mass.
Stable ecosystem
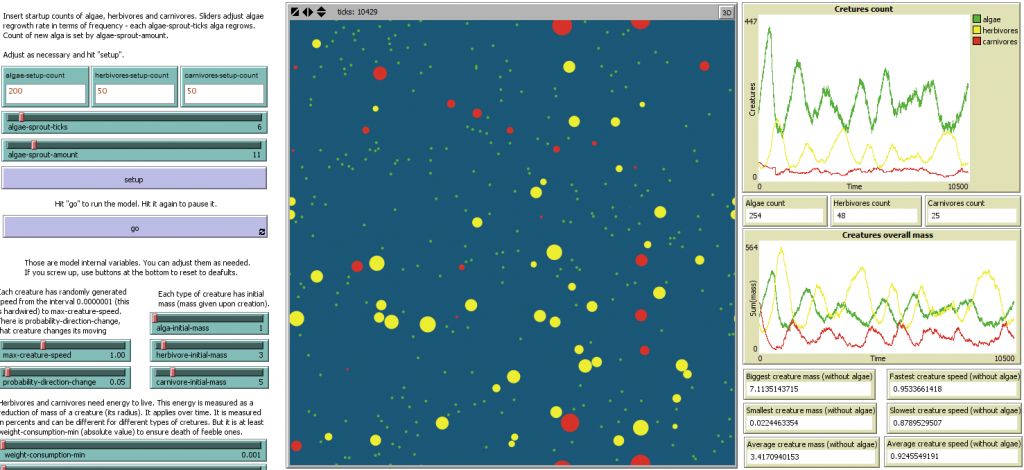
We learned that size of a simulation plane (a puddle of water) has great impact on ecosystem. We gradually raised size of a puddle from 128x128 patches, 5px per patch to 320x320 patches, 2px per patch. This greatly slows the simulation but is necessary to create a body of water where creatures are able to live. When fuzzing input parameters in 320x320 plane, we managed to create a stable ecosystem. We observed, that pathological states occured generally before tick 2000, in very rare cases stretching up to tick 5000. For stable ecosystem, we therefore considered an ecosystem going beyond tick 10000. On the following screenshot is our stable ecosystem.
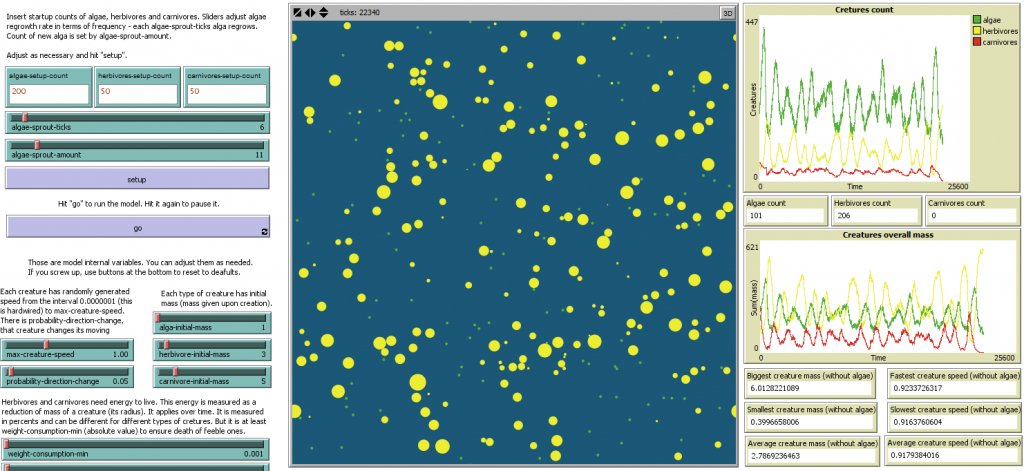
Although even this balance ceased to exist around tick 22000. First, the spatial nature (which is a big difference from predator-prey model) of simulation took place when carnivores weren't able to find anything to eat, which led to overpopulation of herbivores. This led to overpopulation of carnivores and greater decrease of algae population. However, the next "cycle" broke because carnivores almost wiped out herbivores, thus - with almost no food left because they could not find it - carnivores died out and system ended up in PS2.
Finding stable ecosystem parameters
It is safe to say that aforementioned ecosystem is able to survive with all algae, herbivores and carnivores in it. However, a big portion of luck is needed for it to do so. When trying to find smallest stable ecosystem, we used fuzzing - we created a small routine for simulation runs. Routine randomized input parameters across following intervals:
- algae-setup-count - [1;500]
- herbivores-setup-count - [1;100]
- carnivores-setup-count - [1;100]
- algae-sprout-ticks - [1;30]
- algae-sprout-amount - [1;50]
Fuzzing
In total, we examined one hundred randomly generated models. We ran each model one hundred times and if there were still all three creature types alive at the tick 10000, we considered the model as stable. In the end, we computed ecosystem-stability-rate as a number of times we managed to create stable ecosystem divided by 100. Therefore, ecosystem-stability-rate is a probability of creating stable ecosystem when running particular model (each run has random agent placement). We placed results into a CSV file of the structure:
algae-setup-count,herbivores-setup-count,carnivores-setup-count,algae-sprout-ticks,algae-sprout-amount,ecosystem-stability-rate
basically meaning:
{startup parameters of particular model},ecosystem-stability-rate
The result file is attached to this page and link to it can be found in the last section.
Following pseudocode describes our fuzzing procedure (this procedure was ran 100 times to evaluate mentioned 100 different models):
- generate random initial parameters
- run model a hundred times
- run advances to tick 10000; if herbivores or carnivores go extinct earlier, stop earlier
- if there are all three types of creatures still alive, consider model stable
- increment stable-counter
- report model statistics into a csv file
Results
We defined a stable ecosystem as an ecosystem older than 10000 ticks where there are some algae, herbivores and carnivores still alive. First stable ecosystem we found had startup parameters:
- algae-setup-count = 231
- herbivores-setup-count = 52
- carnivores-setup-count = 63
- algae-sprout-ticks = 7
- algae-sprout-amount = 16
By minor tweaking, we were able to lower the parameters a little bit, resulting in smallest ecosystem we managed to find having following parameters. This ecosystem is also shown on previous screenshots.
- algae-setup-count = 200
- herbivores-setup-count = 50
- carnivores-setup-count = 50
- algae-sprout-ticks = 6
- algae-sprout-amount = 11
The balance of whole ecosystem is very fragile. It looks dependent more on a placement and movement of creatures than on their initial count. It basically does not matter whether there are 50 or 60 carnivores, if they are poorly placed e.g. in a proximity of most herbivores, they eat them and stability ceases to exist. This can be partly solved by making puddle even bigger and increase counts of creatures analogically, but it makes NetLogo simulation painfully slow. Creating a stable ecosystem is therefore a matter of coincidence. Probability of creating minimal stable ecosystem is lower than 1% (only one run out of 100 simulation runs).
Truth is, that is not very convincing result. Point is, aforementioned instance was a minimal one. Our fuzzing procedure was able to find much better example with probability of 14% that stable ecosystem forms. This instance har initial parameters:
- algae-setup-count = 468
- herbivores-setup-count = 74
- carnivores-setup-count = 16
- algae-sprout-ticks = 18
- algae-sprout-amount = 24
There is also another instance with probability of about 5% to form a stable ecosystem. Common denominator is that algae-setup-count is over 400 and algae regrowth is relatively fast (about 30 algae every 20 ticks in both cases).
Evolution
During simulation runs, we got a notion that stability of a model can be improved by allowing creatures to have higher maximum speed. Speed is an attribute given to a creature upon its creation and it is random-float from 0 to max-creature-speed + 0.000000000001 which makes every creature move at least a little. Interesting property of this attribute is that when creature splits, the speed is inherited by its offspring. Originally we expected this to have almost no impact on the simulation but, during simulation runs, we managed to observe a simple evolutionary behavior of a system. Consider following starting conditions (carnivores are left out for clarity, effect is also observable when they are present in the model):
- algae-setup-count = 300
- herbivores-setup-count = 100
- carnivores-setup-count = 0
- algae-sprout-ticks = 5
- algae-sprout-amount = 15
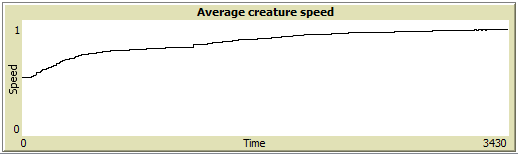
When we look at the average speed of a creature, we can see it is continually rising.
We explain this behavior that creatures start with speed randomly distributed across the interval (approx.) (0,1]. There are almost static creatures, some average ones and very fast ones. Because food is scatterred in the puddle (simulation plane), creature has to encounter it. Those creatures with higher speed can explore larger area of a puddle, eating more and producing more offspring. Slower creatures die out eventually, making also minimal creature speed grow, althouhg the trend is much slower which is given by fact that average is computed over all creatures including many "children" of faster ones and also because slower creatures tend to get smaller to the point when they begin being pushed around by faster ones. Faster creatures also increase the risk of extermination of their prey - the risk of destabilizing whole ecosystem as they can consume more prey than is able to emerge, thus sending ecosystem to a pathological state.
Conclusion
We created a proposed ecosystem model and tested that it is able to function for extended period of time. We found out that using default NetLogo simulation window size does not give creatures enough space to live. After enlarging the canvas to 320x320 patches, 2px per patch, we were able to construct long-term functioning ecosystem spanning for about 22000 ticks - more than twice the time we set as our limit for considering ecosystem as stable. However, stability is really fragile. By re-running the same model one hundred times, we estimated a chance for creating our "minimal stable ecosystem" to be 1% or less (we acomplished this exactly once per one hundred runs).
This is because spatial nature of the simulation. It basically does not matter if we start with 50 or 60 agents, but it is their placement that matters. With smaller simulation planes (like 320x320 we used) it is harder to keep things going and local problems escalate to disasters more easily. When trying to enlarge simulation window even more, we hit performace limits of NetLogo and simulation became too slow to effectively measure anything (time cost of simulation re-runs was too high). Evaluating one particular model (one hundred re-runs up to 10000 ticks each) took about one hour when using 320x320 plane and one 3.5GHz processor core.
We managed to find out following minimal initial parameters for which the ecosystem became, in 1% (or less) cases, stable.
- algae-setup-count = 200
- herbivores-setup-count = 50
- carnivores-setup-count = 50
- algae-sprout-ticks = 6
- algae-sprout-amount = 11
The most stable ecosystem we managed to find is not minimal, but the probability this ecosystem becomes stable is (astonishing) 14%. Its initial parameters are:
- algae-setup-count = 468
- herbivores-setup-count = 74
- carnivores-setup-count = 16
- algae-sprout-ticks = 18
- algae-sprout-amount = 24
In the problem statement, there was a condition that when creatures split, their "childen" inherit speed attribute of a parent. Thanks to this, simple evolutionary pattern emerged in the model - faster creatures were more successful when competing for food and did split themselves more. It also posed a risk of destabilizing whole model because creatures would become too good in consuming their food.
Future development
When simulating we did not cross plane size of 400x400 patches and resorted on plane of size 320x320, 2px per patch as current best choice for results/simulation performance. Unfortunatelly when using few hundred agents we started to hit performance limits of NetLogo platform. Future development of a model could address those issues and, ideally, move whole simulation onto another framework. This would allow us to simulate really big (say 10240x10240) puddles where stability of the whole model could significantly improve as local problems will really stay local problems and possibility of them escalating to global disaster should decrease.
Another direction for improvement could be adressing the importance of creature speed - not only study how max-creature-speed affects whole model, but mainly how evolutionary behavior of model exactly behaves. In our work, we have given just a peek to this area as we noticed there was an emergent behavior in our model. It could be interesting to study impacts of mutation (i.e. slight changes in speed attribute) or imperfect changes (creature does not split exactly in two halves).
Also, our current model does not deal with the process of aging. Creatures do not die other way that they are either eaten or vanish, consuming their whole mass. If the creature actually aged, then it can die and possibly become food for scavengers (new creature-type) or even algae, closing the circle of life between algae, herbivores and carnivores.
Attached files
File:Fisp00 simple-ecosystem.nlogo - This is a source file of whole simulation as described in this text.
File:Fisp00 simple-ecosystem-res.xls - This is a result file from fuzzing models. It contains 100 models (one per line), each was ran 100 times to determine ecosystem-stability-rate - a probability with which particular configuration is able to exist in the long run, beyond tick 10000. Each line of the file contains initial parameters of a model and the last column is ecosystem-stability-rate:
algae-setup-count,herbivores-setup-count,carnivores-setup-count,algae-sprout-ticks,algae-sprout-amount,ecosystem-stability-rate
Petr Fiser (talk) 20:47, 30 May 2016 (CEST)