Difference between revisions of "Mixed strategy"
(→Matching pennies games) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Introduction== | ==Introduction== | ||
{| class="wikitable" align=right width="220" | {| class="wikitable" align=right width="220" | ||
| Line 29: | Line 14: | ||
|} | |} | ||
| − | In his famous paper, John Forbes Nash proved that there is an equilibrium for every finite game. | + | * A '''pure strategy''' is an unconditional, defined choice that a person makes in a situation or game. |
| + | * A '''mixed strategy''' is an assignment of probability to all choices in the strategy set. | ||
| + | |||
| + | The concept of a mixed-strategy was introduced by John von Neumann and Oskar Morgenstern in their 1944 book ''The Theory of Games and Economic Behavior''<ref name="john" />, but their analysis was restricted to the special case of zero-sum games. They showed that a mixed-strategy Nash equilibrium will exist for any zero-sum game with a finite set of actions. | ||
| + | |||
| + | In his famous paper in 1950, John Forbes Nash go further and proved that there is an equilibrium for '''every finite game'''. It can divide Nash equilibria into two types. Pure strategy Nash equilibria are Nash equilibria where all players are playing pure strategies. Mixed strategy Nash equilibria are equilibria where at least one player is playing a mixed strategy. | ||
=== Definition === | === Definition === | ||
Revision as of 11:49, 6 January 2021
Contents
Introduction
| John Forbes Nash Jr. |
|---|
Born:
Died:
|
- A pure strategy is an unconditional, defined choice that a person makes in a situation or game.
- A mixed strategy is an assignment of probability to all choices in the strategy set.
The concept of a mixed-strategy was introduced by John von Neumann and Oskar Morgenstern in their 1944 book The Theory of Games and Economic Behavior[1], but their analysis was restricted to the special case of zero-sum games. They showed that a mixed-strategy Nash equilibrium will exist for any zero-sum game with a finite set of actions.
In his famous paper in 1950, John Forbes Nash go further and proved that there is an equilibrium for every finite game. It can divide Nash equilibria into two types. Pure strategy Nash equilibria are Nash equilibria where all players are playing pure strategies. Mixed strategy Nash equilibria are equilibria where at least one player is playing a mixed strategy.
Definition
Mixed strategy: if the player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} has Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} strategies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1, si2, ...siK} available, a mixed strategy is a distribution of probabilities Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi=(pi1, pi2, ...piK)} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi1} is the probability for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} to choose the strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1} As the mixed strategy is a distribution of probability there is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1}^K pij = 1}
Nash equilibrium in mixed strategy
A mixed strategy Nash equilibrium involves at least one player playing a randomized strategy and no player being able to increase his or her expected payoff by playing an alternate strategy. A Nash equilibrium in which no player randomizes is called a pure strategy Nash equilibrium.
Matching pennies game
Definition
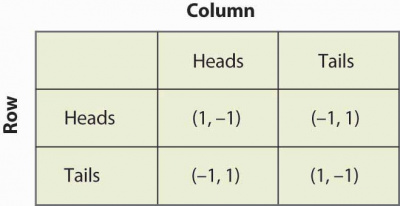
Matching pennies is the name for a simple game used in game theory. It is played between two players. Each player has a penny and must secretly turn the penny to heads or tails. The players then reveal their choices simultaneously. If the pennies match (both heads or both tails), then Row keeps both pennies, so wins one from Column (+1 for Row, −1 for Column). If the pennies do not match (one heads and one tails) Column keeps both pennies, so receives one from Row. The following table display the game.
Mixed strategy in Matching pennies
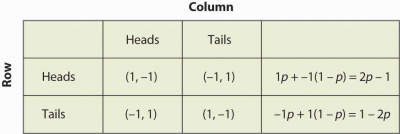
Suppose that Row believes Column plays Heads with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} . If Row plays Heads, he gets 1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} and –1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1-p)} . His expected profit will be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1p - 1(1-p) = 2p - 1 } . This is summarized in Figure below "Mixed strategy in matching pennies".
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p - 1 > 1 - 2p} , then Row is better off, on average, playing Heads than Tails. Similarly. If, on the other hand, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p - 1 = 1 - 2p} it gives Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p=1/2} . Then Row gets the same payoff no matter what Row does. In this case, Row could play Heads, could play Tails, or could flip a coin and randomize Row’s play.
Note that randomization requires equality of expected payoffs. If a player is supposed to randomize over strategy A or strategy B, then both of these strategies must produce the same expected payoff. Otherwise, the player would prefer one of them and wouldn’t play the other.
Battle of the sexes game
Definition
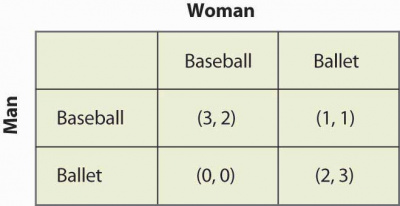
The battle of sexes is a two-players coordination game in the Game theory. In this game there is one man and one woman, the woman prefers going to a ballet and the man prefers going to a baseball game. The nuance here is that they both prefers to go together rather than going alone to his/her prefered activity. The game is described in the table below.
We can highlight the two pure Nash equilibrium: (Ballet, Ballet) and (Baseball, Baseball) you can find them by using the Nash equilibrium course.
Mixed strategy in battle of the sexes
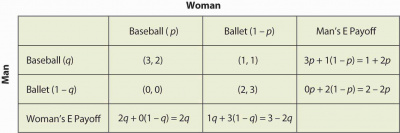
To find the mixed strategy we need to assign some probabilities to each situation. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} be the probability for the woman to go to the baseball game and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} the probability for the men to go to the baseball game. The computations with the expected payoffs for each situation is display below.
The payoff calculations are the same as for the Matching pennies. For example, if the man goes to the baseball game:
- He gets 3 when the woman goes also to the Baseball game, with a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} probability.
- He gets 1 when the woman goes to the Ballet, with a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1-p} probability.
The expected payoff is then just the product of the probability and the payoff, for example for the first row the expected payoff is then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3p + 1(1-p) }
A key aspect in the mixed strategy is the indifference of choosing one or another choice for a player. In the mixed strategy game the Man has to be indifferent between going to the Baseball game and to the Ballet. This indifference or randomization between the choices of a player is expressed mathematically in our example for the man by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1+2p = 2-2p} which yields Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p = 1/4 } . Then if the Woman is going to the Baseball game 1/4 of the time, the Man will be willing to randomize which event he attends. Similar calculation are done for all possibilities and we multiply the probabilities:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p * q}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q * (1-p)}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1-q) * p}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1-q) * (1-p)}
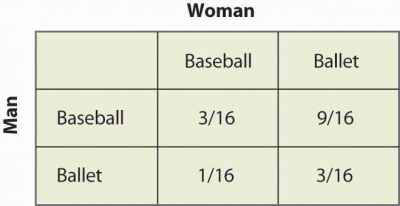
We obtain the following table:
We can note that 9 times over 16 the mixed strategy is (Baseball, Ballet) and it means that they are not together. Even if this mixed strategy Nash equilibrium seems to be undesirable, it's a Nash equilibrium as there is no improvement possible based on the behavior of the other party. This lack of coordination is often a feature of mixed strategy equilibrium. We can now consider another game where a failure of coordination makes more sense, the chicken game.
Chicken game
Definition
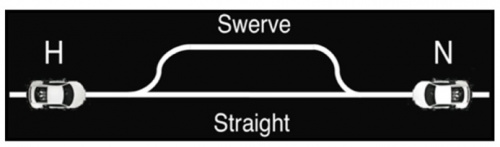
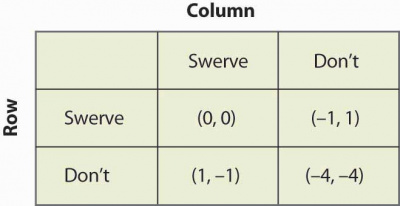
The chicken game in which two players drive two very fast cars towards each other from opposite ends of a long straight road. If one of them swerves before the other, he is called a chicken and will have a payoff of -1. Of course, if neither swerves, they will crash and will get both -4. This is the worst possible payoff. The best payoff is to have your opponent be the chicken, so we assign this a value 1. The last possibility is that both drivers swerve. Then, neither has less honor than the other, so this is a better option than being the chicken. We could assign a payoff matrix to this:
There is again two pure Nash equilibrium here: (Swerve, Don't) and (Don't, Swerve), you can find them by using the Nash equilibrium course.
Mixed strategy in Chicken game
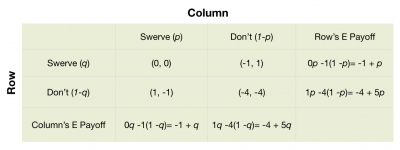
To find the mixed strategy equilibrium we need to assign the same probabilities as for the Battle of the sexes. We can find the table of calculation below.
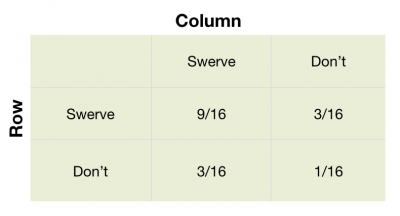
In order to find the mixed strategy equilibrium we have to calculate what probabilities Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} are required to have randomized choices. The same logic as for the Battle of the sexes is applied, we calculate: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0p -1(1-p) = 1p -4(1-p)} and get the optimal probabilities: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p=3/4} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q=3/4} . We just have to multiply these probabilities to obtain the table below.
We can note that the probability of a collision (Don't, Don't) is just 1/16 in the mixed strategy equilibrium. In the chicken game the mixed strategy equilibrium is more likely than in the Battle of the sexes. The whole point in this game is to find out who will yield, which means that it isn't known in advance. This means that the mixed strategy equilibrium is the more reasonable equilibrium.
Mixed strategy in Rock, paper, scissors
Definition
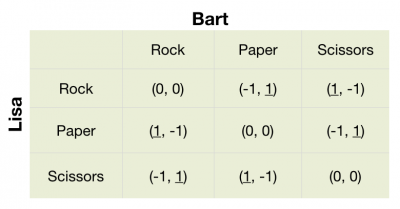
“Rock, paper, scissors” is a child’s game in which two children use their hands to simultaneously choose paper, scissors, or rock. The nature of the payoffs is that paper beats rock, rock beats scissors, and scissors beats paper. This game has the structure that is illustrated below.
We can note that in the game between Bart and Lisa there is no pure Nash equilibrium, because the gains are directly opposed. if Bart received a big utility, Lisa received a small one. If one player knows what will do his opponent, he will directly win. That is why the game has no Nash equilibrium in pure strategy.
The mixed strategy in this game give you the opportunity to protect yourself against the other.
- If Bart choose always Rock, Lisa will always play Paper and Bart will have a utility of -1 with certainty.
- If Bart choose Rock or Paper with a probability of 0.5, Lisa who knows, will play Paper all the time and Bart will get an expected utility of: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0.5 * 0 + 0.5 * (-1) = -0.5} .
- The best strategy for Bart is to choose a probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} for which Lisa is indifferent between choosing Rock, Paper or Scissors. In this case Bart will play Rock, Paper and Scissor with a probability of 1/3 and then Lisa and Bart will both have a utility ofFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1/3) * 1 + (1/3) * 0 + (1/3) * (-1) = 0} .
By choosing a mixed strategy for which Lisa is indifferent between choosing Rock, Paper or Scissors, Bart can increase his utility.
References and Sources
<references>
- ↑ 1.0 1.1 John Von Neumann, Oskar Morgenstern. Theory of Games and Economic Behavior. 1944. Book review: https://www.ams.org/journals/bull/1945-51-07/S0002-9904-1945-08391-8/S0002-9904-1945-08391-8.pdf.
- ↑ John Forbes Nash Jr, Non-cooperative games. Article 1950. https://www.jstor.org/stable/1969529?seq=1
https://cs.stanford.edu/people/eroberts/courses/soco/projects/1998-99/game-theory/chicken.html https://en.wikipedia.org/wiki/Strategy_(game_theory) https://saylordotorg.github.io/text_introduction-to-economic-analysis/s17-03-mixed-strategies.html https://en.wikipedia.org/wiki/Theory_of_Games_and_Economic_Behavior https://www.jstor.org/stable/1969529?seq=1