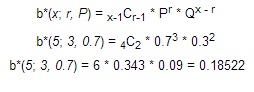Difference between revisions of "Distributions/cs"
(→Diskrétní rozdělení pravděpodobnosti) |
(→Spojité rozdělení pravděpodobnosti) |
||
| Line 59: | Line 59: | ||
* Oblast ohraničená křivkou funkce hustoty a na ose x je rovna 1. | * Oblast ohraničená křivkou funkce hustoty a na ose x je rovna 1. | ||
* Pravděpodobnost, že náhodná veličina nabývá hodnoty mezi a a, b se rovná oblasti pod funkcí hustoty ohraničené a a b . | * Pravděpodobnost, že náhodná veličina nabývá hodnoty mezi a a, b se rovná oblasti pod funkcí hustoty ohraničené a a b . | ||
| + | |||
| + | Typy rozdělení: | ||
| + | * Rovnoměrné rozdělení | ||
| + | * Normální (Gaussovo) rozdělení – normované a obecné | ||
| + | * Logaritmicko-normální | ||
| + | * Cauchyovo rozdělení | ||
| + | * Exponenciální rozdělení | ||
| + | * Gama rozdělení | ||
| + | * Beta rozdělení | ||
| + | * Rozdělení chí-kvadrát | ||
| + | * Studentovo t-rozdělení | ||
| + | * (Fisherovo) F-rozdělení | ||
=Příklady diskrétních rozdělení= | =Příklady diskrétních rozdělení= | ||
Revision as of 22:19, 31 May 2014
Úvod
Změříme-li nějakou veličinu, jde z hlediska teorie o náhodný pokus. Předpis, který přiřazuje každému výsledku našeho náhodného pokusu určité číslo, se nazývá náhodná veličina. Z matematického hlediska je tedy náhodná veličina (x) reálná funkce definovaná na množině všech elementárních jevů (jednotlivé možné výsledky pokusu), která každému jevu přiřadí reálné číslo. Pravděpodobnost, s kterou náhodná proměnná nabývá určité hodnoty nebo je obsažena v určitém intervalu hodnot se nazývá pravděpodobnostní rozdělení.
Pro vysvětlení principu je vhodné použít nejklasičtější příklad. Hod mincí se sledováním výsledku, co padlo, je vlastně provedení náhodného pokusu. Definičním oborem (možnými výsledky) tohoto pokusu jsou dva výsledky - první možnost = padne líc (panna); - druhá možnost = padne rub (orel). Obor hodnot je v tomto případě množina {0,1}. Pro tuto situaci vlastně definiční obor a obor hodnot splývají, ale nemusí tomu obvykle tak být. Rozdělení pravděpodobnosti náhodné veličiny tedy získáme, pokud každé hodnotě diskrétní náhodné veličiny, popř. intervalu hodnot spojité náhodné veličiny, přiřadíme pravděpodobnost.
Obecně platí, že ve statistice se používají velká písmena k reprezentování náhodné proměnné a malá písmena, představují jednu z jejich hodnot. Například, X představuje náhodné proměnné x. P (X) představuje pravděpodobnost X. P (X = x), se vztahuje k pravděpodobnosti, že náhodná proměnná X je rovna na určitou hodnotu, označené x. Jako příklad lze uvést, P (X = 1), se vztahuje k pravděpodobnosti, že náhodná proměnná X je rovno 1.
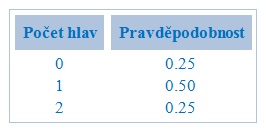
Modifikovaným příkladem s hodem mincí bude jasně znázorněn vztah mezi náhodnými proměnnými a rozdělením pravděpodobnosti a zároveň se svým způsobem vracíme k našemu úvodu. Představte si, že hodit mincí dvakrát. Tento jednoduchý statistický experiment může mít čtyři možné výsledky: HH, HL, LH, a LL. Nyní proměnná X představuje počet hlav, které padnou při tomto experimentu. Proměnná X může nabývat hodnot 0, 1, nebo 2. V tomto příkladu, X je náhodná proměnná, protože jeho hodnota je určena na základě výsledků statistického experimentu. Rozdělení pravděpodobnosti je tabulka, nebo rovnice, která spojuje jednotlivé výsledky statistické experimentu s jeho pravděpodobností výskytu. V následující tabulce, která sdružuje výsledky s pravděpodobností, je předveden příklad rozdělení pravděpodobnosti.
Výše uvedená tabulka představuje rozdělení pravděpodobnosti náhodné proměnné X.
Typy rozdělení
Diskrétní rozdělení pravděpodobnosti
Je-li náhodná veličina, diskrétní veličina, její rozdělení pravděpodobnosti se nazývá diskrétní rozdělení pravděpodobnosti. Příkladem se opět vracíme k hodu mincí. Tento jednoduchý statistický experiment může mít čtyři možné výsledky: HH, HL, LH, a LL. Nyní, ať náhodná veličina X představuje počet hlav, které vyplývají z tohoto experimentu. Náhodná veličina X se může uskutečnit pouze na základě hodnot 0, 1, nebo 2, takže je diskrétní náhodná veličina.
Výše uvedená tabulka představuje diskrétní rozdělení pravděpodobnosti, protože se týká každé hodnoty diskrétní náhodné veličiny s pravděpodobností výskytu. U diskrétního rozdělení pravděpodobnosti platí, že každá možná hodnota diskrétní náhodné veličiny může být spojena s nenulovou pravděpodobností. Potom platí, že diskrétní rozdělení pravděpodobnosti může být vždy prezentováno ve formě tabulky.
Typy rozdělení:
- Diracovo rozdělení
- Rovnoměrné rozdělení
- Alternativní (Bernoulliovo, nula-jedničkové) rozdělení
- Binomické rozdělení
- Geometrické rozdělení
- Hypergeometrické rozdělení
- Poissonovo rozdělení
- Negativně binomické rozdělení
Spojité rozdělení pravděpodobnosti
Je-li náhodná veličina veličinou spojitou, její rozdělení pravděpodobnosti se nazývá spojité rozdělení pravděpodobnosti . Spojité rozdělení pravděpodobnosti se liší od diskrétního rozdělení pravděpodobnosti v několika ohledech.
- Pravděpodobnost, že spojitá náhodná proměnná bude předpokládat určitou hodnotu, je nulová.
- V důsledku toho kontinuální rozdělení, pravděpodobnost nelze vyjádřit ve formě tabulky.
- Místo toho se používá k popisu kontinuálního rozdělení pravděpodobnosti rovnice nebo vzorec.
Nejčastěji používaná rovnice kontinuálního rozdělení pravděpodobnosti se nazývá funkce hustoty pravděpodobnosti. Pro toto rozdělení pravděpodobnosti má funkce hustoty následující vlastnosti:
- Vzhledem k tomu, že spojitá náhodná proměnná je definována přes kontinuální rozsah hodnot (tzv. domény proměnné), bude graf funkce hustoty kontinuální v tomto rozsahu.
- Oblast ohraničená křivkou funkce hustoty a na ose x je rovna 1.
- Pravděpodobnost, že náhodná veličina nabývá hodnoty mezi a a, b se rovná oblasti pod funkcí hustoty ohraničené a a b .
Typy rozdělení:
- Rovnoměrné rozdělení
- Normální (Gaussovo) rozdělení – normované a obecné
- Logaritmicko-normální
- Cauchyovo rozdělení
- Exponenciální rozdělení
- Gama rozdělení
- Beta rozdělení
- Rozdělení chí-kvadrát
- Studentovo t-rozdělení
- (Fisherovo) F-rozdělení
Příklady diskrétních rozdělení
Alternativní rozdělení
Týká se náhodných veličin, které mohou mít pouze dva různé výsledky. Pravděpodobnost jednoho z nich je p, druhého 1 − p. Značení tohoto rozdělení A(p).
Příklad 1:
Zmiňovaný hod mincí s p=0,5 a možnými výsledky {0,1},
Příklad 2:
V pytlíku máme tři kuličky černé barvy a jednu bílé barvy, výsledkem pokusu bude vytažení černé či bílé kuličky, bíle s pravděpodobností p = 0,25 a bílé s pravděpodobností 1-p = 0,75.
Rovnoměrné rozdělení
Binomické rozdělení
Binomický experiment (také známý jako Bernoulliho zákon) je statistický experiment , který má následující vlastnosti:
- Experiment se skládá z "n" opakovaných pokusů.
- Každý proces může vyústit v pouhých dvou možných výsledků. Říkáme, že jeden z těchto výsledků je úspěch a další, selhání.
- Pravděpodobnost úspěchu, označujeme P.
- Fyzikální zákony jsou nezávislé a to znamená, že výsledek v jedné studii neovlivní výsledek v jiných studiích.
Veličina s binomickým rozdělením je tedy součtem nezávislých veličin s rozdělením alternativním, parametry tohoto rozdělení jsou tedy jednak "p" a poté ještě počet pokusů "n". Toto rozdělení se typicky značí jako Bi(n,p). Pravděpodobnostní funkce vypadá takto:
kde x může nabývat hodnot 0, 1, 2 až n.
Příklad: Počet šestek při hodu 3 kostkami. Například pravděpodobnost, že padne jedna šestka je:
Negativní binomické rozdělení
Negativní binomický experiment je statistický experiment , který má následující vlastnosti:
- Experiment se skládá z x opakovaných pokusů.
- Každý proces může vyústit do pouhých dvou možných výsledků. Říkáme jeden z těchto výsledků je úspěch a další, selhání.
- Pravděpodobnost úspěchu, označme P rovnost fyzikálních zákonů.
- Zákony jsou nezávislé ; to znamená, že výsledek v jedné studii neovlivní výsledek v jiných studiích.
- Experiment pokračuje až R je pozorování úspěchů, kde r je určena předem.
Podívejme se na následující statistický experiment. Opakovaně jste hodili mincí a spočtěte, kolikrát mince přistane na hlavě. Můžete pokračovat, dokud mince přistane na hlavě 5 krát N. To je dáno tím, že jde o negativní binomické experiment:
- Experiment se skládá z opakovaných pokusů. Opakovaně jsme hodili mincí, dokud přistála 5krát na hlavě.
- Každý proces může mít za následek jen dva možné výsledky - panna nebo lev.
- Pravděpodobnost úspěchu je konstantní - 0,5 na každé zkoušce.
- Pravidla jsou nezávislá; To znamená, že výsledky mezi jednotlivými experimenty se navzájem neovlivní.
- Experiment pokračuje, dokud se neobjevil pevný počet úspěchů; v tomto případě 5 hlav.
Negativní binomická náhodná proměnná je číslo "X" opakovaných zkoušek k produkci "r" úspěchů v negativní binomické experimentu. Rozdělení pravděpodobnosti negativního binomického rozdělení náhodné veličiny se nazývá negativní binomické rozdělení . Negativní binomické rozdělení je také známé jako distribuce Pascal.
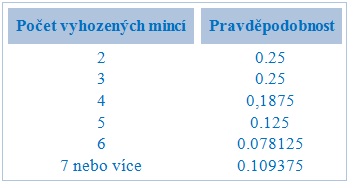
Předpokládejme, že opakovaně házíme mincí a počítáme počet hlav (úspěchů). Budeme-li pokračovat házením mincí, dokud nepadne l 2 krát hlava, provádíme negativní binomický experiment. Negativní binomická náhodná proměnná je počet mincí požadovaných k dosažení 12 hlav. V tomto příkladu je množství hodů náhodná proměnná, která může mít libovolné celé číslo mezi 12 a nekonečnem. Negativní binomické rozdělení pravděpodobnosti pro tento příklad je uvedeno v tabulce:
Příklad:
Bob je vysokoškolský basketbalový hráč. Má 70% úspěšnost ve střelbě na koš. To znamená, že jeho pravděpodobnost bodování je 0,70. Jaká je pravděpodobnost, že Bob během sezóny dá 3 koše z pěti pokusů (hodů) po sobě jdoucích?
Řešení:
Toto je příklad negativního binomického experimentu. Pravděpodobnost úspěchu ( P ) je 0,70, počet pokusů ( x ) je 5 a počet úspěchů ( r ) je 3.
Chcete-li tento problém vyřešit, musíte doplnit hodnoty do negativního binomického vzorce.
To znamená, že pravděpodobnost, že Bob dá své tři úspěšné hody z pěti pokusů je 0,18522.
Poissonovo rozdělení
Toto rozdělení vyplývá z Poissonova experimentu. Poisson experiment je statistický experiment , který má následující vlastnosti:
- Experiment má za následek výsledky, které mohou být klasifikovány jako úspěchy či neúspěchy.
- Je známo, že průměrný počet úspěchů (μ), který se vyskytuje v určitém regionu.
- Pravděpodobnost, že dojde k úspěchu, je úměrná velikosti regionu.
- Pravděpodobnost, že dojde k úspěchu ve velmi malé oblasti, je v podstatě nulová.
Všimněte si, že zadaná oblast může mít mnoho podob. Například, to může být délka, plocha, objem, doba, atd. Použití: Počet úrazů za určitý interval, počet tiskových chyb na jedné stránce, počet branek za fotbalový zápas, počet vadných výrobků za časový interval, atd.
Předpokládejme, že provádíme Poisson experiment, ve kterém je μ průměrný počet úspěchů v daném regionu. Potom pravděpodobnost Poisson je:
P ( x , μ) = (e -μ ) (μ x ) / x!
kde x je skutečný počet úspěchů, které vyplývají z experimentu, a e je přibližně rovna 2,71828.
Příklad:
Průměrný počet prodaných domů od firmy „Xena nemovitosti s.r.o.“ je 2 domy za den. Jaká je pravděpodobnost, že přesně 3 domy budou zítra prodány?
Řešení:
Toto je Poissonův experiment, v němž víme následující:
μ = 2; že 2 domy se prodávají za den v průměru.
x = 3; protože chceme zjistit pravděpodobnost, že tři domy budou zítra prodány.
e = 2.71828; protože e je konstanta rovná přibližně 2,71828.
Doplňme tyto hodnoty do Poissonova vzorce:
P ( x , μ) = (e -μ ) (μ x ) / x!
P (3, 2) = (2,71828 -2 ) (2 3 ) / 3!
P (3, 2) = (0,13534) (8 ) / 6
P (3, 2) = 0,180
To znamená, že pravděpodobnost prodeje 3 domů zítra je 0,180.