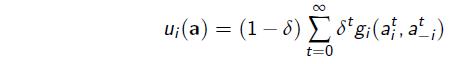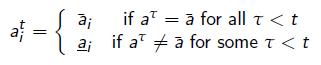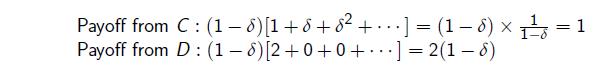Repeated games
Contents
Introduction
In previous chapters of Game theory we introduced One-shot games like Prisoner's dilemma. In other words situations when we are allowed to do one action that result in some outcome (payoff). For example a situation when someone wants to enjoy fast car ride. If he drives really fast he enjoys fast ride and he´s happy but he also rist that police will catch him and arrest. So he must choose between driving fast or not fast according to his ulitily from one decision. But in the real world we often meet situations that repeat or their consequences affect other situations. We can say that our live is set of games in some order and we are playing them. And all of us know that this games, this situations repeat very often. We go to work every day or go shopping for example. Sequence of games that affect other games and are played by the same players is called repeated game. [1]
We can say that every human is rational and follows his own profit. That in other words mean that a person should not have problem with betrayal of other person to get higher payoff. But what if game continues and this betrayal can be avenger? Under these circumstances is the first person willing to betray the second in the first round? It depends on the situation. It depends on the payoff. So we can say that in a game of various number of persons we can achieve cooperation for a time that players benefit from cooperation.
Game theory is often quoted by politicians to gave their opinios seriousness and as a way how to look smarter that they are.[2] And it is also a great example of repeated game. Politicians like senators often vote about laws they propose. Options for the vote are support or not to support. If the vote was only a matter of good proposal/bad proposal, politicians would vote exactly the same. But because they follow their own goals the vote depends on many different things. Lets say that senator A propose a law that after the adoption brings a great popularity to him. But he needs senator B to support his proposal. So he asks senator B for support and he agrees only on the condition that he will in return later vote for his proposal. Regardless of what they promised to each other they now have several options. Senator B can vote for proposel and than expect support for his proposal or defect already in round 1, gain some profit from senator A not having that popularity but senator A will be probably angry and not support his proposal too. If he chooses to support him now have senator A some options. He has gained popularity for his law proposal and he can now return the favor or betray. Remember he already gained popularity so he can make additional profit from betraying his opponent. But if he do so he can probably expect revenge every time he wants to cooperate with senator B. There will be surely more voting in the future so what is the best strategy to maximize the payoff? That is the knowledge we gain from studying repeated games.
The Evolution of Cooperation
The evolution of cooperation can refer to:
- the study of how cooperation can emerge and persist (also known as cooperation theory) as elucidated by application of game theory
- a 1981 paper by political scientist Robert Axelrod and evolutionary biologist W. D. Hamilton in the scientific literature [3]
- a 1984 book by Axelrod that expanded on the paper and popularized the study. [4]
Application of game theory
Game theory and mathematical analysis of behaviour have gained great popularity mainly due to a period of the WW2 and the Cold War. In 1944 John von Neumann and Oskar Morgenstern published famous Theory of Games and Economic Behavior. [5] This book explained how to use game theory for analyzing and developing optimal strategies for military, economy and other purposes. The Cold War was also a great period for game theory usage. US government funded teams that should analyze possible strategies and practices against the enemy. There were two hostile countries capable of total destruction of each other. This state is from view of game theory incredibly interesting. Lets assume the situation that one side lauches nuclear rockets. Rockets gonna hit targets in minutes so second side of conflict has the opportunity to launch counterattack. But it is really necessary to launch nuclear attack? In few minutes they are gonna be dead anyway so they don´t have to care what will be after them because even their children will be dead. So retaliatory nuclear strike would only killed milions of people. So what is the point of launching it? Revenge? And if not, what is the point of even having nuclear weapons? The fact is that not having the opportunity to fatal strike is already case of loosing in the Cold War. Many people today agrue if one of side would actually use nuclear weapons in no matter how escalated situation. Reason to have nuclear weapons is most definitely the threat. But what is the point of threat if our enemy know that we are not gonna use them. Well the enemy must not know this. That is the reason why US presindents and high-ranked military officiers were instructed to act on public a little "crazy and insane" to prove that they will launch the attack no matter what.
Robert Axelrod and his tournaments
| Robert Axelrod |
|---|
Born:
Robert Axelrod is the Walgreen Professor for the Study of Human Understanding at the University of Michigan. He has appointments in the Department of Political Science and the Gerald R. Ford School of Public Policy. Prior to coming to Michigan he taught at the University of California, Berkeley (1968-74). He holds a BA in mathematics from the University of Chicago (1964), and a PhD in political science from Yale (1969). He is best known for his interdisciplinary work on the evolution of cooperation which has been cited more than 30,000 times. |
In 1981 Robert Axelrod published article dealing with the fundamental question: When should a person cooperate, and when should be person selfish, in an ongoing interaction with another person? He used a simple way to represent the type of situation that gives rise to these problems. He explained everything on the particular kind of game called the iterated Prisoner´s Dilemma. [3]
In the same year Robert Axelrod also held a computer tournament in which 15 different strategies for repeated prisoner's dilemma, sent by leading game theorists, competed with each in the game of 200 routes (total of 15 × 15 games). Payout was always calculated as the sum of the basis matrix: [4]
Strategie in the tournament
In addition to the strategies Always Cooperates and Always Defects Axelrod divided strategies used into the following groups: [4]
- Nice strategies - never betray the first (only in retaliation)
- Dirty strategies - at least sometimes betray first
- Relief Strategies - can reciprocate, but has a short memory, forgets the old sins
- Unforgiving strateges - never forget old wrongs, never break from the cycle of mutual retaliation even against conciliatory opponent
- Strategies without envy - only thing that matters is profit, beating the opponent is not important
- Envy strategies - the goal is to defeat the opponent
To the great surprise of all participants gained the most points very simple strategy "tit for tat" , which sent Anatol Rapoport a psychologist and expert on the game theory.
tit for tat - In the first round cooperates and in other rounds repeats the move of opponent.
Finitely Repeated Games
The game is played for a finite and known number of rounds, for example, 2 rounds/repetitions.
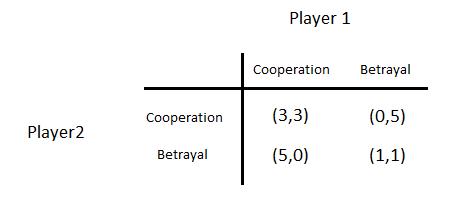
Lets recall PD game.
What happens if this game was played T < ∞ times? We first need to decide what the equilibrium notion is. Natural choice, subgame perfect Nash equilibrium (SPE). Recall: SPE ⇐⇒ backward induction. Therefore, start in the last period, at time T . What will happen?
Dominant strategy for the last period is "defect" regardless of the history of the game. The subgame that has the start at time point T has dominant strategy equilibrium "defect,defect". We move to stage T - 1. We now by backward induction that at T players play "defect,defect". So subgame T - 1 has also dominant strategy equilibrium. Knowing this we can say that there exists a unique subgame perfect equilibrium "defect,defectL at each date.
Theorem
Consider repeated game G T (δ) for T < ∞. Suppose that the stage game G has a unique pure strategy equilibrium a∗. Then G T has a unique SPE. In this unique SPE, at = a∗ for each t = 0,1,..., T regardless of history. [1]
Infinitely Repeated Games
The game has no predetermined length. Players act as though it will be played indefinitely or it ends only with some probability. This type of game is interesting but unlike finitely repeated they are not rare. How often we find a situation that we know exactly when it gonna ends and what it will be like? On the other hand, we routinely play many games that are infinitely repeated. Our goal is to find subgame perfect equilibrias in these types of games.
Because we eliminated backward inducion from the model, now we can see that under these circumstances (neither player knows when the game ends) cooperation (strategy vector {N,N}) becomes the equilibrium solution for both players. As we know the solution is always not only one. In this case there is more equilibrium solutions and we call this Folk Theorems. [1]
The first folk theorem states that any attainable individual and rational pay-vector can be repeated game Nash equilibrium. Second folk theorem says that achievable payout vector that Pareto dominates any payroff vector of single game equilibrium can be SPE of repeated game.
Strategies
Unlinke finitely repeated there are many possible strategies to play. We discussed some of them above in the article. Lets just sum well-known strategies for repeated PD: [6]
- Always Cooperates
- Always Defects
- Grudger, Spiteful
- Tit for Tat
- Mistrust
- Naive Prober
- Remorseful Prober
- Hard Tit for Tat
- Gradual
- Gradual Killer
- Hard Tit for 2 Tats
- Soft Tit for 2 Tats
- Slow Tit for Tat
- Periodically DDC
- Periodically CCD
- Soft Majority
- Hard Majority
- Pavlov´s
- Pavlov´s Pn
- Random
- Hard Joss
- Soft Joss
- Generous Tit for Tat
- Better and Better
- Worse and Worse
Trigger strategies
Now consider the infinitely-repeated game Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{G}^{\infty} } , players play the game repeatedly at times t
The notation ![]() now denotes the (infinite) sequence of action profiles.
now denotes the (infinite) sequence of action profiles.
A period-t history is ![]() (action profiles at all periods before t), and the set of all period-t histories is
(action profiles at all periods before t), and the set of all period-t histories is ![]() .
.
A pure strategy for player i is ![]() , where
, where ![]()
The payoff to player i for the entire repeated game is then
Note: this summation is well defined because ![]() .
.
The term (1 − δ) is introduced as a normalization, to measure stage and repeated game payoffs in the same units.
* The normalized payoff of having a utility of 1 per stage is 1.
Now lets add trigger strategies to this model.
In infinitely-repeated games we can consider trigger strategies. [1] [7] A trigger strategy essentially threatens other players with a “worse,” punishment, action if they deviate from an implicitly agreed action profile.
A non-forgiving trigger strategy (or grim trigger strategy) s would involve this punishment forever after a single deviation. A non-forgiving trigger strategy (for player i) takes the following form:
Here ![]() is the implicitly agreed action profile and
is the implicitly agreed action profile and ![]() is the punishment action.
is the punishment action.
This strategy is non-forgiving since a single deviation from ![]() induces player i to switch to
induces player i to switch to ![]() forever.
forever.
Lets recall PD game.
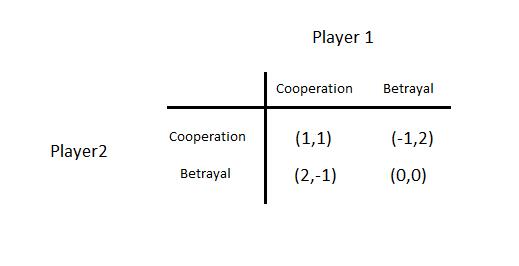 Suppose this game is played infinitely often. Is “Both defect in every period” still an SPE outcome? Suppose both players use the following non-forgiving trigger strategy s∗:
Suppose this game is played infinitely often. Is “Both defect in every period” still an SPE outcome? Suppose both players use the following non-forgiving trigger strategy s∗:
* Play C in every period unless someone has ever played D in the past * Play D forever if someone has played D in the past.
Lets show next that the preceding strategy is an SPE if δ ≥ 1/2 usingone-stage deviation principle.
Assuption 1: cooperation is best response to cooperation
Suppose that there has so far been no D. Then given s∗ being played by the other player, the payoffs to cooperation and defection are:
Cooperation better if ![]() . This shows that for
. This shows that for ![]() , deviation to defection is not profitable.
, deviation to defection is not profitable.
Assumption 2: defection is best response to defection
Suppose that there has been some D in the past, then according to s∗, the other player will always play D. Against this, D is a best response.
This argument is true in every subgame, so s∗ is a subgame perfect equilibrium. Cooperating in every period would be a best response for aplayer against s∗. But unless that player herself also plays s∗, her opponent would not cooperate. Thus SPE requires both players touse s∗.
Example 1
New product
Example that we have 2 companies that want to launch a new product. The product is similar and they can launch it the same day because it is from the same chinesse factory. So the volume of sales will be determined by price. Companies have 5 days until product launch and every day they can reveal their price to the market at the same hour. Lets find NE.
Due to backward induction we know that after last day there will be no punishment for not cooperating. So last day both companies choose {B,B}. Forth day they know that they will choose {B,B} last day and again choose {B,B}. And this state continues every day till they reach first day again with NE strategy {B,B}.
Example 2
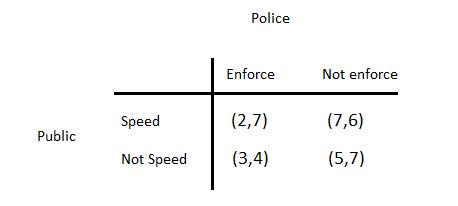
Law enforcement
The police is trying to enforce speed limit at some specific location with this payoff matrix:
The equilibrium mixed strategies are p* = 0.75 and q* = 0.66. Expected payoffs are u(public) = 3.63 and u(police) = 6.25. In (Not speed, Not enforce) they are both better off.
Strategies
Police: e-trigger
t = 0: Play Not enforce
t > 0: Play Not enforce if all previous outcomes were (Not speed, Not enforce). Use the mixed strategy q* otherwise
Public: n-trigger
t = 0: Play Not speed
t > 0: Play Not speed if all previous outcomes were (Not speed, Not enforce). Use the mixed strategy p* otherwise
Equilibrium
Police:
- If it follows its strategy: 7
- It is never profitable to deviate
Public:
- If it follows its strategy: 5
The pair of strategies is SPE
References
<references> [1] [2] [3] [4] [5] [6] [7]
- ↑ 1.0 1.1 1.2 1.3 1.4 Osborne, Martin J.; Rubinstein, Ariel (1994). A Course in Game Theory. Cambridge: MIT Press. ISBN 0-262-15041-7.
- ↑ 2.0 2.1 Scheve, Tom (2010). How Game Theory Works. howstuffworks.com [online].
- ↑ 3.0 3.1 3.2 Axelrod, Robert (1981). Science, New Series, Vol. 211, No. 4489. (Mar. 27, 1981), pp. 1390-1396.
- ↑ 4.0 4.1 4.2 4.3 Axelrod, Robert (1984), The Evolution of Cooperation, Basic Books, ISBN 0-465-02122-0.
- ↑ 5.0 5.1 Copeland, A. H. (1945). "Review: Theory of Games and Economic Behavior by John von Neumann and Oskar Morgenstern". Bull. Amer. Math. Soc. 51 (07): 498–504.
- ↑ 6.0 6.1 Hyšková, Magdalena (2011). Přednášky - Teorie her 6. Opakované hry. FD ČVÚT v Praze.
- ↑ 7.0 7.1 Ozdaglar, Asu (2010). 6.254 : Game Theory with Engineering Applications. Lecture 15: Repeated Games. MIT EDU Press.